Как обозначается угол наклона в физике: Как вычислить угол наклона 🚩 как найти угол наклона в физике 🚩 Естественные науки

Расчет и нанесение уклона на обмерных чертежах » Лазерное сканирование и архитектурные обмеры в Санкт-Петербурге | НПП «Фотограмметрия»

С необходимостью посчитать уклон постоянно сталкиваются проектировщики, строители, архитекторы, а также люди ряда других профессий, в силу того, что на земной поверхности очень трудно найти идеально ровный участок. Уклон выражается в градусах или в процентах. Обозначение в градусах показывает угол кривизны поверхности. Но уклон может быть представлен и в виде тангенса этого угла, умноженного на 100%.

Как рассчитать уклон поверхности?
Уклон – это отношение превышения (ВС) к заложению (АС) и обозначается в текстовых документах буквой i.
Например, i=1:6

Разделите противолежащий катет (вертикальное расстояние) на прилежащий (расстояние между точками). Если вам нужно получить уклон в процентах, умножьте полученное число на 100%. Чтобы получить уклон в промилле, умножьте результат деления на 1000‰.

Если вам необходимо получить уклон в градусах, воспользуйтесь тем, что полученный при делении катетов результат – тангенс угла наклона. Посчитайте его арктангенс при помощи инженерного калькулятора, в результате вы получите значение уклона в градусах.

На видах (фасадах), разрезах, сечениях и схемах перед размерным числом, определяющим величину уклона, наносят знак , острый угол которого должен быть направлен в сторону уклона.
Обозначение уклона наносят непосредственно над линией контура или на полке линии-выноски.
На планах направление уклона плоскостей указывают стрелкой, на которой, при необходимости, проставляют величину уклона (см.рис.).

Построение и обозначение уклона. Пример изображения уклона на планах.

Величину уклона (тангенс угла наклона) указывают в виде простой или десятичной дроби с точностью до третьего знака.

Уклон (в строительстве) — показатель крутизны склона (а также ската кровли).

Укло́н (в геодезии) — показатель крутизны склона; отношение превышения местности к горизонтальному проложению, на котором оно наблюдается.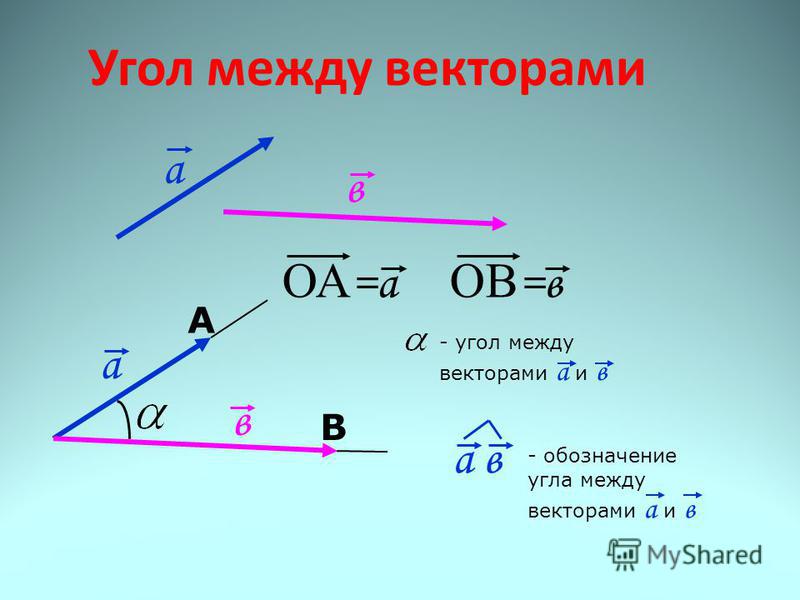 Иными словами, величина уклона равна тангенсу угла между поверхностью склона и горизонталью.

Уклон поверхности равен тангенсу угла α, tgα = h/l — отношение перпендикуляра, опущенного из точки поверхности на прямую поверхность, к длине прямой поверхности от начала склона (при вершине угла α) до перпендикуляра.

Например, подъёму 12 м на 100 м перемещения по горизонтали соответствует уклон, равный 0,12 (12 % или 120 ‰).
При чтении нотации знак «%» произносится «сотых», а «‰» — «тысячных».

Источник:

книга: Единые требования по выполнению строительных чертежей.
М.: Изд-во «Архитектура-С», 2004.
Справочное пособие.
Автор: Георгиевский О.В.

Аннотация:
Справочное пособие по строительному черчению для студентов средних и высших учебных заведений. Пособие выполнено в соответствии с требованиями ГОСТов.
Настоящее справочное пособие выполнено в соответствии с требованиями ГОСТов ЕСКД (Единой системы конструкторской документации) и СПДС (Системы проектной документации для строительства).
Пособие может быть использовано при выполнении заданий по архитектурно-строительному черчению, а также при выполнении курсовых и дипломных проектов студентами всех строительных специальностей средних и высших учебных заведений.

Распечатать

Механическая работа — определение, формула, виды, свойства

Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.

Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.

Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.

Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.

Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.

Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.

Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.

Для совершения работы необходимы два условия:

• чтобы на тело действовала сила,
• чтобы происходило перемещение тела.

Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.

Запомнить!

Работа равна нулю, если:

• при приложенной силе перемещение отсутствует;
• сила не приложена и тело перемещается по инерции;
• угол между векторами силы и перемещения равен 90°.

Полезная и затраченная работа

Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».

Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.

Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.

Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.

И как же достоверно определить, какая работа полезная, а какая затраченная?

Все очень просто! Задаем два вопроса:

1. За счет чего происходит процесс?

2. Ради какого результата?

В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).

Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.

Мощность

На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.

Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.

Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.

Также для мощности справедлива другая формула:

Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.

Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Примеры решения задач

Задача 1

Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:

1. Выталкивающая сила.

2. Сила вязкого трения.

3. Сила тяжести.

4. Ни одна из перечисленных сил.

Решение

Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.

Ответ: 3.

Задача 2

Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью.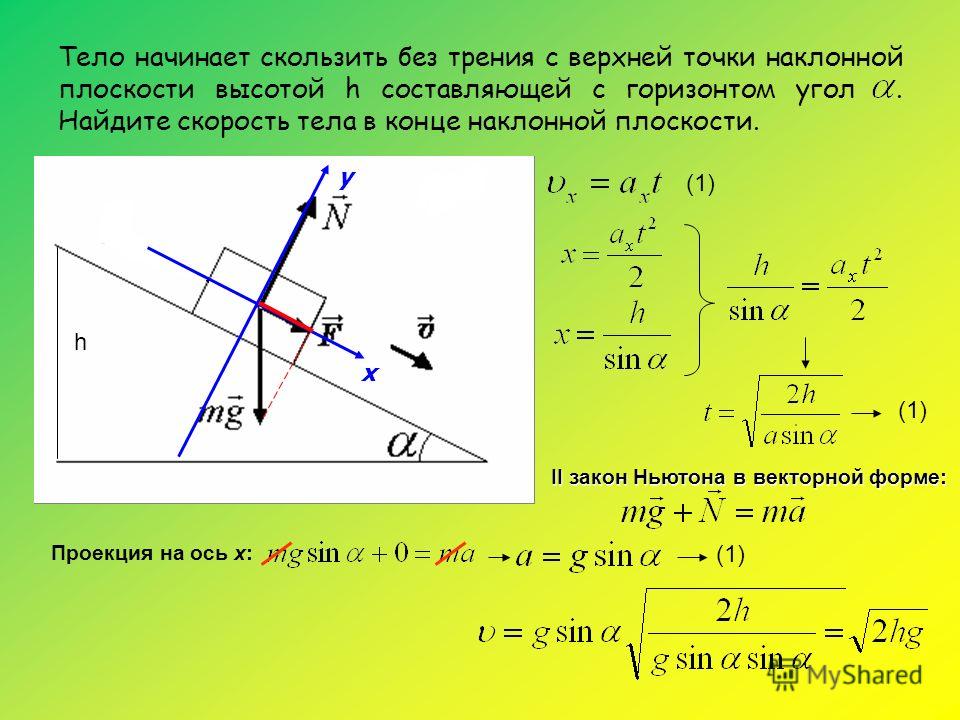 Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?

Решение

Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:

Ответ: 3200 Дж.

Задача 3

Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?

Решение

В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.

Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:

A = Fl = 30 * 5 = 150 Дж

Ответ: 150 Дж.

Задача 4

Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости v^x тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?

Решение

На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.

Мощность можно найти по формуле N = Fv.

N = FV = 2×5 = 10 Вт

Ответ: 10 Вт.

Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!

Угол наклона в задачах по физике

Автор: The Experts at Dummies и

Обновлено: 26 марта 2016 )

Физика I: 501 Практические задачи для чайников (+ Бесплатная онлайн-практика)

Исследовать книгу Купить на Amazon

В физике, если объект толкают вниз по склону, угол наклона склона влияет на ускорение объекта. Например, когда вы толкаете сани с покрытого льдом холма, вы можете рассчитать угол наклона холма, зная массу и ускорение саней.

Вес — гравитационная сила, с которой Земля воздействует на объект. У поверхности Земли вес равен массе, умноженной на 9,8 метра в секунду в квадрате. величина силы трения равна коэффициенту трения, умноженному на величину нормальной силы. Трение всегда препятствует относительному движению двух поверхностей.

Вот несколько практических вопросов, которые помогут проиллюстрировать эту концепцию.

Практические вопросы

1. 25-килограммовые санки скользят по склону, покрытому ледяным снегом. Если сани движутся вниз по склону со скоростью 4,8 метра в секунду в квадрате, каков угол наклона холма по отношению к горизонтали?

   Предположим, что снег представляет собой поверхность без трения, и округлите ответ до ближайшего целого градуса.

2. Саманта толкает дочь, сидящую на санках, вниз по заснеженной горке с постоянным уклоном с силой 50 ньютонов. Сани разгоняются до 1,9метров в секунду в квадрате. Если общая масса ее дочери и санок равна 40 кг, каков угол наклона горки?

   Округлите ответ до ближайшего градуса.

Ответы

Ниже приведены ответы на практические вопросы:

1. 29 градусов.

   Сначала нарисуйте диаграмму свободного тела:

   Только одна сила направлена ​​вдоль оси движения

   , так что это единственный вклад в чистое ускорение вдоль поверхности холма:

2. 4 степени.

   Три силы участвуют ( F _N , Нормальная сила; F _G , Сила из -за

   6666666666666666666666666666666 2 _{66666666666666666666 2 6666666166666666666666666666 2}

   66666666666666666666666666 2 . сила толчка Саманты). Нарисуйте диаграмму свободного тела, показывающую векторы и любые необходимые компоненты, чтобы выровнять силы по двум перпендикулярным осям:

   Сани движутся вдоль оси, параллельной поверхности холма, так что это направление ускорения вам нужно изучить. Суммируя силы в этом направлении:

   (В этой установке в качестве положительного направления используется «вниз по склону».) По второму закону Ньютона

Об этой статье

Эта статья из книги:

• Физика I: 501 Практические задачи для чайников (+ Бесплатная онлайн-практика),

Об авторе книги:

Эту статью можно найти на категория:

• Физика,

Наклонные плоскости

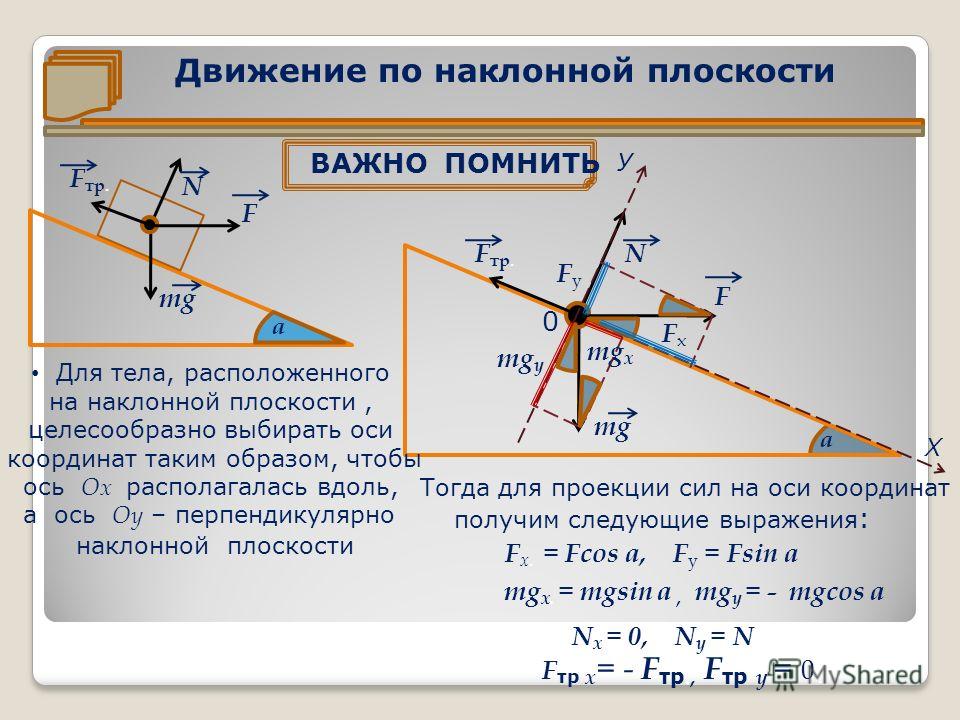
Объект, помещенный на наклонная поверхность часто скользит по поверхности. Скорость, с которой объект скользит по поверхности, зависит от того, насколько наклонена поверхность; чем больше наклон поверхности, тем выше скорость, с которой объект будет скользить по ней.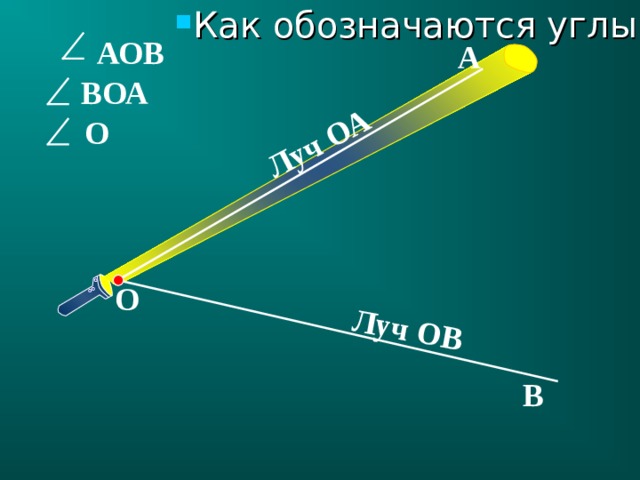 В физике наклонная поверхность называется наклонной плоскостью. Известно, что объекты ускоряются вниз по наклонным плоскостям из-за неуравновешенной силы. Чтобы понять этот тип движения, важно проанализировать силы, действующие на объект на наклонной плоскости. На диаграмме справа показаны две силы, действующие на ящик, расположенный на наклонной плоскости (предполагается, что трение отсутствует). Как показано на диаграмме, их всегда 9.0005 не менее двух сил

, действующих на любой объект, расположенный на наклонной плоскости, — сила тяжести и нормальная сила. Сила тяжести (также известная как вес) действует в направлении вниз; однако нормальная сила действует в направлении, перпендикулярном поверхности (на самом деле нормаль означает «перпендикулярно»).

Аномальная нормальная сила

Первая особенность задач с наклонной плоскостью состоит в том, что нормальная сила равна , а не направлен в ту сторону, к которой мы привыкли.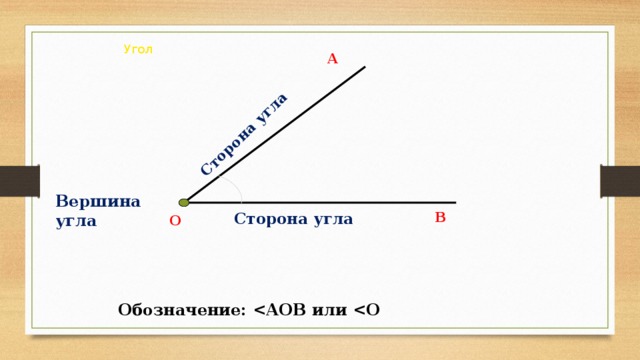 До этого момента в курсе мы всегда видели нормальные силы, действующие в восходящем направлении, противоположном направлению силы тяжести. Но это только потому, что объекты всегда находились на горизонтальных поверхностях, а не на наклонных плоскостях. Правда о нормальных силах заключается не в том, что они всегда направлены вверх, а в том, что они всегда направлены перпендикулярно поверхности, на которой находится объект.

Компоненты силы тяжести

Задача определения результирующей силы, действующей на объект на наклонной плоскости, является сложной задачей, поскольку две (или более) силы не направлены в противоположные стороны. Таким образом, одну (или несколько) сил придется разложить на перпендикулярные составляющие, чтобы их можно было легко добавить к другим силам, действующим на объект. Обычно любую силу, направленную под углом к ​​горизонтали, разлагают на горизонтальную и вертикальную составляющие.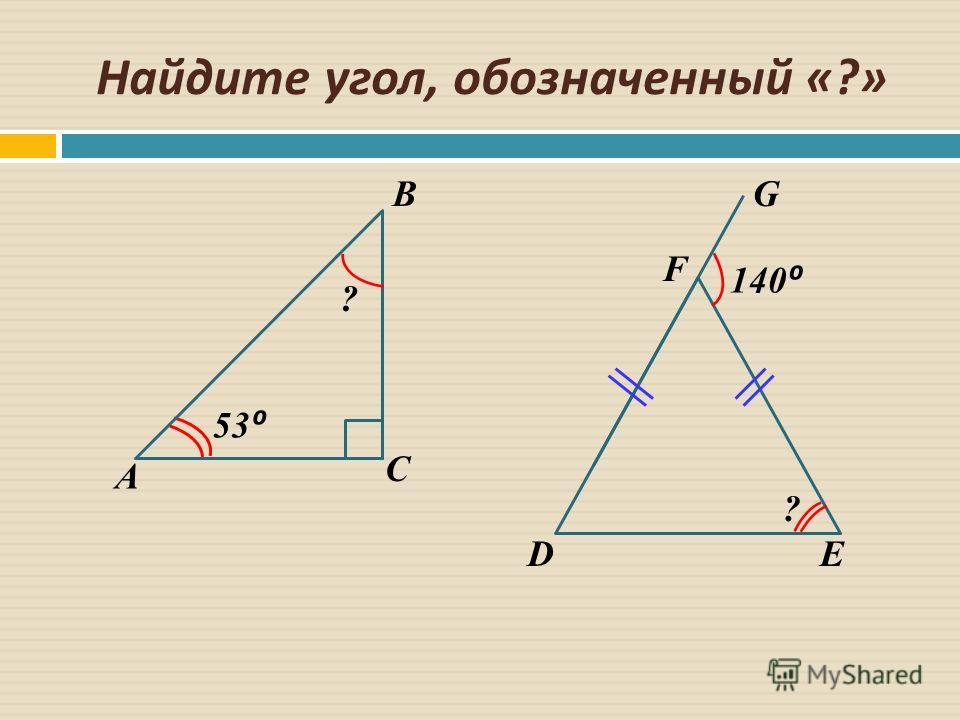 Однако это не тот процесс, который мы будем проводить с наклонными плоскостями. Вместо этого процесс анализа сил, действующих на объекты на наклонных плоскостях, будет включать определение весового вектора (F _грав ) на две перпендикулярные составляющие. Это вторая особенность задач наклонной плоскости. Сила тяжести будет разложена на две составляющие силы — одну, направленную параллельно наклонной поверхности, и другую, направленную перпендикулярно наклонной поверхности. На приведенной ниже диаграмме показано, как сила тяжести была заменена двумя составляющими — параллельной и перпендикулярной составляющей силы.

Перпендикулярная составляющая силы тяжести направлена ​​против нормальной силы и, таким образом, уравновешивает нормальную силу. Параллельная составляющая силы тяжести не уравновешивается никакой другой силой. Этот объект впоследствии будет ускоряться вниз по наклонной плоскости из-за наличия неуравновешенной силы. Именно параллельная составляющая силы тяжести вызывает это ускорение. Параллельная составляющая силы тяжести является результирующей силой.

Задача определения величины двух составляющих силы тяжести — это простой способ использования уравнений. Уравнения для параллельной и перпендикулярной составляющих:

При отсутствии трения и других сил (растяжения, приложенных и т. д.) ускорение объекта на наклонной поверхности равно значению параллельной составляющей (м *g*синус угла), деленное на массу (m). Это дает уравнение

Упрощение задачи о наклонной плоскости

При наличии трения или других сил (приложенной силы, силы натяжения и т. д.) ситуация несколько усложняется. Рассмотрим схему, показанную справа. Перпендикулярная составляющая силы по-прежнему уравновешивает нормальную силу, поскольку объекты не ускоряются перпендикулярно наклону.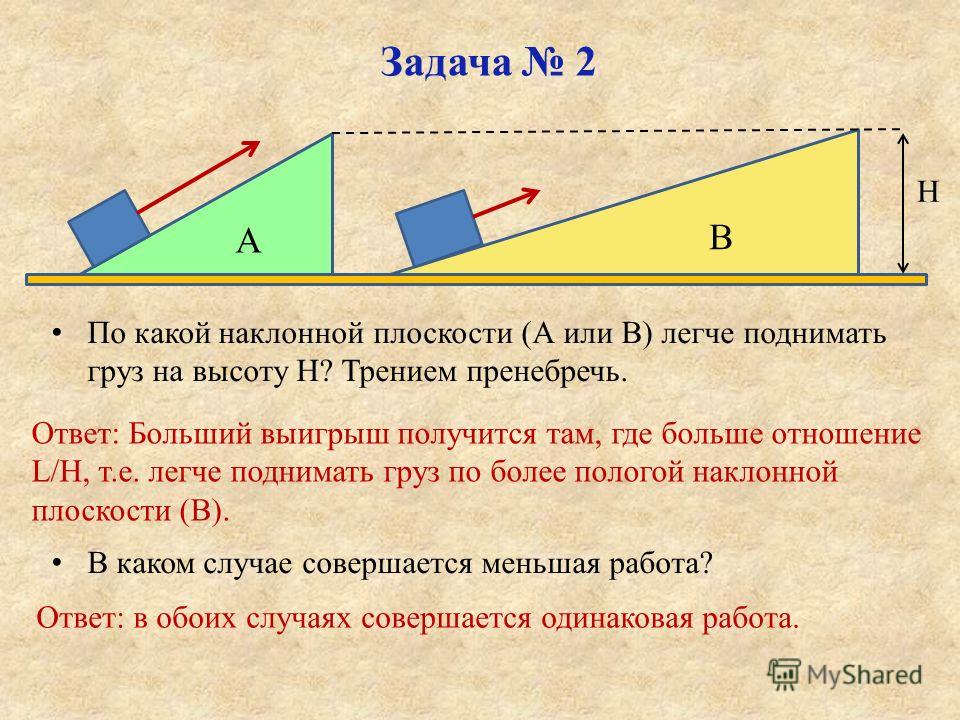 Тем не менее, сила трения также должна учитываться при определении чистой силы. Как и во всех задачах о чистой силе, чистая сила представляет собой векторную сумму всех сил. То есть все отдельные силы складываются вместе как 9.0115 векторов . Перпендикулярная составляющая и нормальная сила в сумме дают 0 Н. Параллельная составляющая и сила трения в сумме дают 5 Н. Суммарная сила равна 5 Н и направлена ​​вдоль наклона к полу.

Приведенную выше задачу (и все задачи с наклонной плоскостью) можно упростить с помощью полезного приема, известного как «наклон головы». Задача о наклонной плоскости во всех отношениях похожа на любую другую задачу о результирующей силе, за исключением того, что поверхность была наклонена . Таким образом, чтобы преобразовать проблему обратно в более удобную для вас форму, достаточно наклонить голову в том же направлении, в котором наклон был наклонен . Или, еще лучше, просто наклоните страницу бумаги (верное лекарство от TNS — «синдром наклонной шеи» или «синдром тако-шеи»), чтобы поверхность больше не казалась ровной.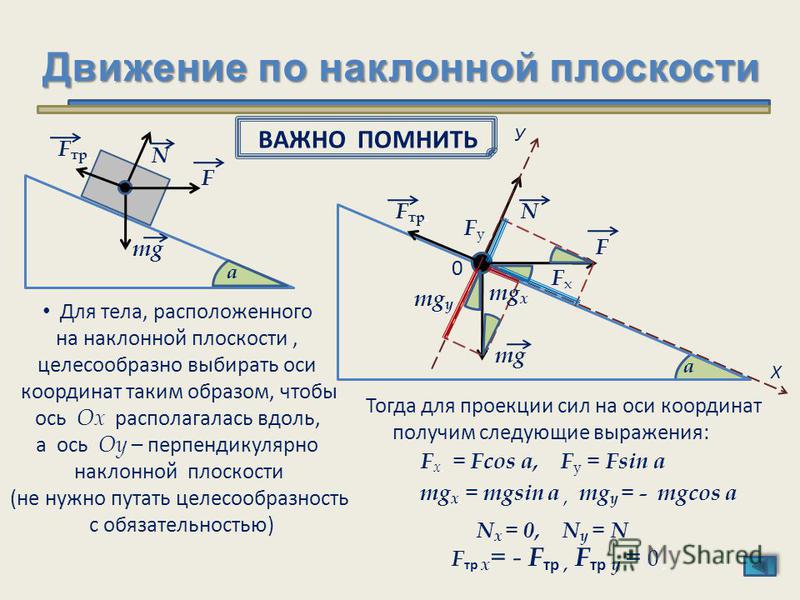 Это показано ниже.

После того, как сила тяжести будет разделена на две составляющие и наклонена наклонная плоскость, задача должна выглядеть очень знакомо. Просто игнорируйте силу гравитации (поскольку она была заменена двумя ее компонентами) и найдите результирующую силу и ускорение.

В качестве примера рассмотрим ситуацию, изображенную на диаграмме справа. На диаграмме свободного тела показаны силы, действующие на 100-килограммовый ящик, скользящий по наклонной плоскости. Плоскость наклонена под углом 30 градусов. Коэффициент трения между обрешеткой и склоном равен 0,3. Определить результирующую силу и ускорение ящика.

Начнем с вышеуказанной задачи, найдя силу тяжести, действующую на ящик, и компоненты этой силы, параллельные и перпендикулярные наклону. Сила тяжести равна 980 Н, а компоненты этой силы равны F _{параллельно} = 490 Н (980 Н • sin 30 градусов) и F _{перпендикулярно} = 849 Н (980 Н • cos30 градусов). Теперь нормальную силу можно определить равной 849 Н (она должна уравновешивать перпендикулярную составляющую вектора веса). Силу трения можно определить по величине нормальной силы и коэффициента трения; F _трение составляет 255 Н (F _трение = «mu»*F _норма = 0,3 • 849 Н). Чистая сила представляет собой векторную сумму всех сил. Силы, направленные перпендикулярно наклону, уравновешивают; силы, направленные параллельно наклону, не уравновешиваются. Чистая сила составляет 235 Н (490 Н — 255 Н). Ускорение составляет 2,35 м/с/с (F _net /м = 235 Н/100 кг).

На двух приведенных ниже диаграммах показана диаграмма свободного тела для 1000-килограммовых американских горок при первом падении двух разных аттракционов на американских горках. Используйте приведенные выше принципы векторного разрешения, чтобы определить результирующую силу и ускорение автомобилей американских горок. Предположим, что влияние трения и сопротивления воздуха пренебрежимо мало. Когда закончите, нажмите кнопку, чтобы просмотреть ответы.

Влияние угла наклона на ускорение американских горок (или любого объекта на склоне) можно наблюдать в двух вышеприведенных практических задачах. С увеличением угла увеличивается ускорение объекта. Объяснение этого относится к компонентам, которые мы рисовали. По мере увеличения угла составляющая силы, параллельная наклону, увеличивается, а составляющая силы, перпендикулярная наклону, уменьшается. Именно параллельная составляющая вектора веса вызывает ускорение. Таким образом, ускорения больше при больших углах наклона. На приведенной ниже диаграмме показано это соотношение для трех различных углов возрастающей величины.

Немного физики американских горок

Американские горки вызывают два острых ощущения, связанных с начальным падением по крутому склону. Острые ощущения от ускорения создаются за счет использования больших углов наклона при первом падении; такие большие углы увеличивают значение параллельной составляющей вектора веса (составляющей, вызывающей ускорение). Ощущение невесомости производится за счет уменьшения величины нормальной силы до значений, меньших их обычных значений. Важно признать, что ощущение невесомости — это чувство, связанное с более низкой, чем обычно, нормальной силой. Как правило, человек весом 700 Н испытывает нормальную силу 700 Н, когда сидит на стуле. Однако, если кресло движется с ускорением вниз по наклону в 60 градусов, то человек будет испытывать нормальную силу в 350 ньютонов. Это значение меньше нормального и способствует ощущению, что вес меньше нормального, т. е. 9.0134 невесомость .

Используйте виджет ниже, чтобы исследовать другие ситуации с наклонной плоскостью.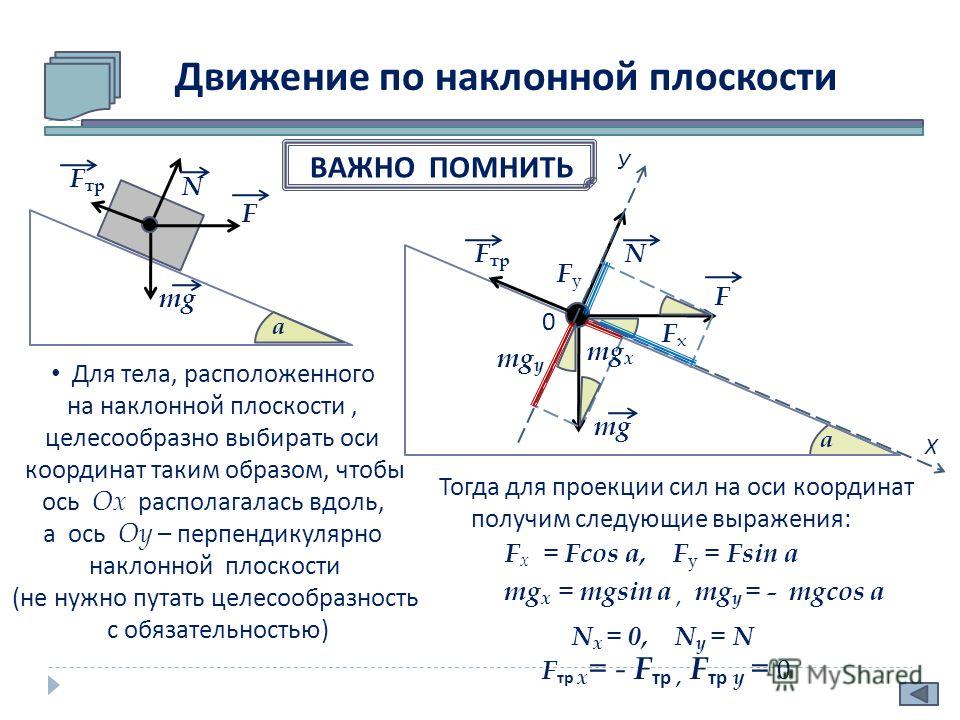 Просто введите массу, угол наклона и коэффициент трения (используйте 0 для случаев отсутствия трения). Затем нажмите кнопку Отправить , чтобы просмотреть ускорение.

Следующие вопросы предназначены для проверки вашего понимания математики и концепций наклонных плоскостей. После того, как вы ответили на вопрос, нажмите кнопку, чтобы увидеть ответы.

1. Два мальчика играют в хоккей на соседней улице. Бродячая шайба движется по льду без трения , а затем поднимается по наклонной дороге без трения. Какая из следующих бегущих строк (A, B или C) точно изображает движение шайбы, когда она движется по ровной улице, а затем вверх по подъездной дорожке?

Объясните свой ответ.

2. Маленький Джонни стоит внизу подъездной дорожки и пинает футбольный мяч. Мяч катится на север по подъездной дорожке, а затем возвращается к Джонни. Какой из следующих графиков зависимости скорости от времени (A, B, C или D) наиболее точно отображает движение мяча, когда он катится вверх по подъездной дорожке и обратно?

Объясните свой ответ.

3. Мяч для гольфа катится по горизонтальному участку грина на 18-й лунке. Затем он сталкивается с крутым нисходящим уклоном (см. Диаграмму). Участвует трение. Какой из следующих шаблонов бегущей строки (A, B или C) может быть подходящим представлением движения мяча?

Объясните, почему неуместные шаблоны неуместны.

4. Восьмой фрейм Мисси де Пенн в боулинг-лиге по средам стал катастрофой. Мяч скатился с полосы, прошел через грузовой люк в задней части здания, а затем по подъездной дорожке. Милли Митер (товарищ по команде Мисси), которая проводила каждую свободную минуту за подготовкой к экзамену по физике, начала визуализировать график зависимости скорости от времени для движения мяча. Какой из графиков зависимости скорости от времени (A, B, C или D) будет подходящим представлением движения мяча, когда он катится по горизонтальной поверхности, а затем вниз по склону? Рассмотрим силы трения.

5. Три партнера по лаборатории — Олив Н. Гленво, Глен Брук и Уоррен Пис — обсуждают задачу о наклоне (см. схему). Они спорят о значении нормальной силы. Олив утверждает, что нормальная сила равна 250 Н; Глен утверждает, что нормальная сила равна 433 Н; а Уоррен утверждает, что нормальная сила равна 500 Н. Хотя все три ответа кажутся разумными, правильным является только один. Укажите, какие два ответа неверны, и объясните, почему они неверны.

6. Лон Скейпер возится с газоном, когда из его тачки вырывается 2-килограммовая шина и начинает катиться вниз по крутому холму (уклон 30°) в Сан-Франциско. Нарисуйте параллельные и перпендикулярные компоненты этого весового вектора.