Как оценить точность измерений: Оценка точности измерений » Лазерное сканирование и архитектурные обмеры в Санкт-Петербурге | НПП «Фотограмметрия»

Оценка точности измерений » Лазерное сканирование и архитектурные обмеры в Санкт-Петербурге | НПП «Фотограмметрия»

1. Оценку точности измерений производят
— предварительно до начала измерений путем обработки результатов специально выполненных наблюдений;
— после окончания измерений путем обработки результатов наблюдений, выполненных в процессе этих измерений.

2. Для оценки точности измерений используют многократные наблюдения параметра в одном из установленных сечений (мест) или двойные наблюдения параметра в разных сечениях (местах) одного или нескольких объектов измерений.

Общее число наблюдений М, необходимое для оценки точности результата измерений, составляет:
для предварительной оценки — 20;
для оценки точности выполненных измерений — не менее 6.

Для уменьшения влияния систематических погрешностей измерения выполняют в соответствии с требованиями настоящего стандарта (ГОСТ 26433.0-85):
Наблюдения производят в прямом и обратном направлениях, на разных участках шкалы отсчетного устройства, меняя установку и настройку прибора и соблюдая другие приемы, указанные в инструкции по эксплуатации на средства измерения. При этом должны быть соблюдены условия равноточности наблюдений (выполнение наблюдений одним наблюдателем, тем же методом, с помощью одного и того же прибора и в одинаковых условиях).
Перед началом наблюдений средства измерений следует выдерживать на месте измерений до выравнивания температур этих средств и окружающей среды.

3. Оценку точности измерений производят путем определения действительной погрешности измерения и сравнения ее с предельной погрешностью .
В случаях, когда нормирована относительная погрешность измерения, определяют действительную относительную погрешность.

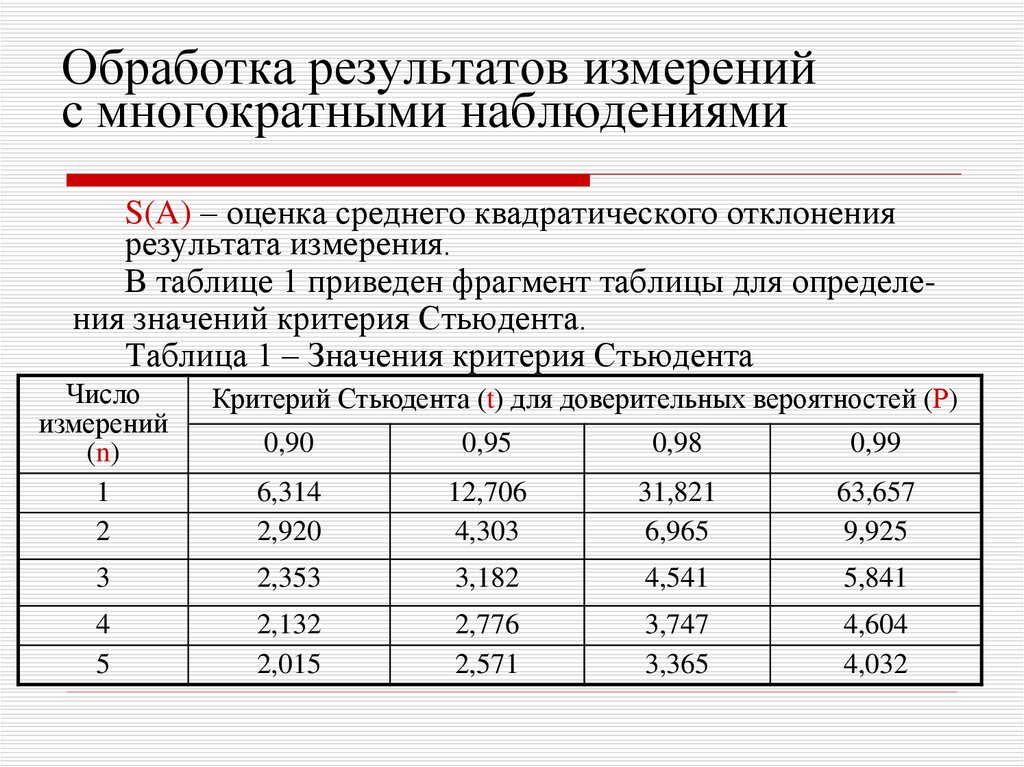
4. Действительную погрешность измерения при многократных наблюдениях определяют по формуле

Таблица 1.

Среднюю квадратическую погрешность измерения при многократных наблюдениях параметра определяют по формуле

Если при измерениях используются средства и методы, для которых из специально выполненных ранее измерений или из эксплуатационной документации установлена средняя квадратическая погрешность наблюдения , то действительную погрешность измерения определяют по формуле

5. Действительную погрешность результата измерения при двойных наблюдениях параметра в одном из установленных сечений (местах) оценивают по формуле

где вычисляемая величина — это абсолютное значение остаточной систематической погрешности, численное значение которой определено из обработки ряда двойных наблюдений.

6. При двойных наблюдениях близких по значению линейных размеров среднюю квадратическую и остаточную систематическую погрешность результата измерения определяют в соответствии с табл. 2. При этом имеется ввиду, что наблюдения являются равноточными в паре и между парами.

Таблица 2.

Обозначения, принятые в табл. 3:
х1 и х2 — результаты первого и второго наблюдений в паре параметра в одном из установленных сечений (мест). Для обеспечения правильной оценки все первые наблюдения в установленных сечениях (местах) выполняют в одном направлении (или при одной установке прибора) и все вторые — в обратном направлении (или при симметричной установке прибора), а запись результатов наблюдений — в строгом соответствии с порядком их выполнения;

7. При двойных наблюдениях, существенно различных по значению между парами линейных размеров, среднюю квадратическую и остаточную систематическую погрешность результата измерений определяют в соответствии с табл. 3. При этом наблюдения в паре являются равноточными, а между парами — неравноточными.

Таблица 3.

Обозначения, принятые в табл. 5:
С — любая постоянная величина;
остальные — см. выше.

Распечатать

Оценка точности измерений » Лазерное сканирование и архитектурные обмеры в Санкт-Петербурге | НПП «Фотограмметрия»

Приложение 3 (рекомендуемое) к ГОСТу 26433.0-85 ПРАВИЛА ВЫПОЛНЕНИЯ ИЗМЕРЕНИЙ

1. Оценку точности измерений производят:
— предварительно до начала измерений путем обработки результатов специально выполненных наблюдений;
— после окончания измерений путем обработки результатов наблюдений, выполненных в процессе этих измерений.

2. Для оценки точности измерений используют многократные наблюдения параметра в одном из установленных сечений (мест) или двойные наблюдения параметра в разных сечениях (местах) одного или нескольких объектов измерений.

Общее число наблюдений M, необходимое для оценки точности результата измерений, составляет:

для предварительной оценки — 20;
для оценки точности выполненных измерений — не менее 6.

Для уменьшения влияния систематических погрешностей измерения выполняют в соответствии с требованиями п.6.6 настоящего стандарта.

Прочитать п. 6.6. из ГОСТа 26433.0-85 ПРАВИЛА ВЫПОЛНЕНИЯ ИЗМЕРЕНИЙ

3. Оценку точности измерений производят путем определения действительной погрешности измерения

и сравнения ее с предельной погрешностью

В случаях, когда нормирована относительная погрешность измерения, определяют действительную относительную погрешность.

4. Действительную погрешность измерения при многократных наблюдениях определяют по формуле

,
где

— средняя квадратическая погрешность измерения;

t — коэффициент (принимают по табл. 1).

Среднюю квадратическую погрешность измерения при многократных наблюдениях параметра определяют по формуле

Если при измерениях используются средства и методы, для которых из специально выполненных ранее измерений или из эксплуатационной документации установлена средняя квадратическая погрешность наблюдения
, то действительную погрешность измерения определяют по формуле

5. Действительную погрешность результата измерения при двойных наблюдениях параметра в одном из установленных сечений (местах) оценивают по формуле

где — абсолютное значение остаточной систематической погрешности, численное значение которой определено из обработки ряда двойных наблюдений.

Пример.
Произвести предварительную оценку точности измерений длинномером длины изделий при контроле точности их изготовления. Измерение длины каждого изделия в процессе контроля будут выполняться при числе наблюдений m = 2.
Выполняют многократные наблюдения длины одного изделия при числе наблюдений М = 20. Для уменьшения влияния систематической погрешности первые десять наблюдений выполняют в одном направлении каждый раз со сдвигом шкалы рулетки на 70 — 90 мм, а вторые десять наблюдений — в другом направлении с тем же сдвигом шкалы.
Результаты наблюдений и последовательность их обработки приведены в табл. 2 (для упрощения приведены результаты только 10 наблюдений, т.е. М = 10).

Принимаем х = 3205,0 с ошибкой округления а = -0,2; х0 — наименьший результат из всех наблюдений, х0 =3200.

Контроль правильности вычислений:

Среднюю квадратическую погрешность результата измерений находят по формуле 2 настоящего приложения

Действительная погрешность измерения

Предельную погрешность измерения находят по формуле (2) настоящего стандарта. При допуске на длину 20 мм

Проверяем соблюдение условия (1) настоящего стандарта: 5,0 > 4,0 мм.
Действительная погрешность измерения не соответствует требуемой, должны быть приняты другие средства измерений или увеличено количество наблюдений m. Принимаем m = 4, тогда

6. При двойных наблюдениях близких по значению линейных размеров среднюю квадратическую и остаточную систематическую погрешность результата измерения определяют в соответствии с табл. 3. При этом имеется ввиду, что наблюдения являются равноточными в паре и между парами.

Обозначения, принятые в табл. 3:

— результаты первого и второго наблюдений в паре параметра в одном из установленных сечений (мест). Для обеспечения правильной оценки все первые наблюдения в установленных сечениях (местах) выполняют в одном направлении (или при одной установке прибора) и все вторые — в обратном направлении (или при симметричной установке прибора), а запись результатов наблюдений — в строгом соответствии с порядком их выполнения;

Пример.

Произвести оценку точности измерений, выполненных методом бокового нивелирования двойными наблюдениями при контроле отклонений от разбивочных осей низа 7 смонтированных колонн. Произведено 7 пар наблюдений при двукратной установке теодолита над центром пункта пространственной геодезической сети, которые являются равноточными в паре и между парами. Результаты наблюдений и последовательность их обработки приведены в табл. 4.

Вычисляют остаточную систематическую погрешность и проверяют ее значимость:

Проверка правильности вычислений

Средняя квадратическая погрешность результата измерения

Действительная погрешность измерения

t = 3 при М = 14 и доверительной вероятности 0,99.
Предельная погрешность измерения при допуске совмещения ориентиров при установке колонн ▲x = 24 по ГОСТ 21779-82

Проверяем соблюдение условия (1) настоящего стандарта: 3,9 мм Действительная точность соответствует требуемой.

7. При двойных наблюдениях, существенно различных по значению между парами линейных размеров, среднюю квадратическую и остаточную систематическую погрешность результата измерений определяют в соответствии с табл. 5. При этом наблюдения в паре являются равноточными, а между парами — неравноточными.

Обозначения, принятые в табл. 5:
С — любая постоянная величина;
остальные — см. выше.

Пример.
Произвести оценку точности измерений, выполняемых рулеткой при контроле точности детальных разбивочных работ двойными наблюдениями расстояний между разбивочными осями.
Наблюдения в паре равноточны, а между парами, вследствие большой разницы в значениях расстояний, неравноточны.
Выполнено 8 пар наблюдений (по числу имеющихся в натуре ориентиров).

Вычисляют остаточную систематическую погрешность и проверяют ее значимость

Следовательно, остаточной систематической погрешностью можно пренебречь.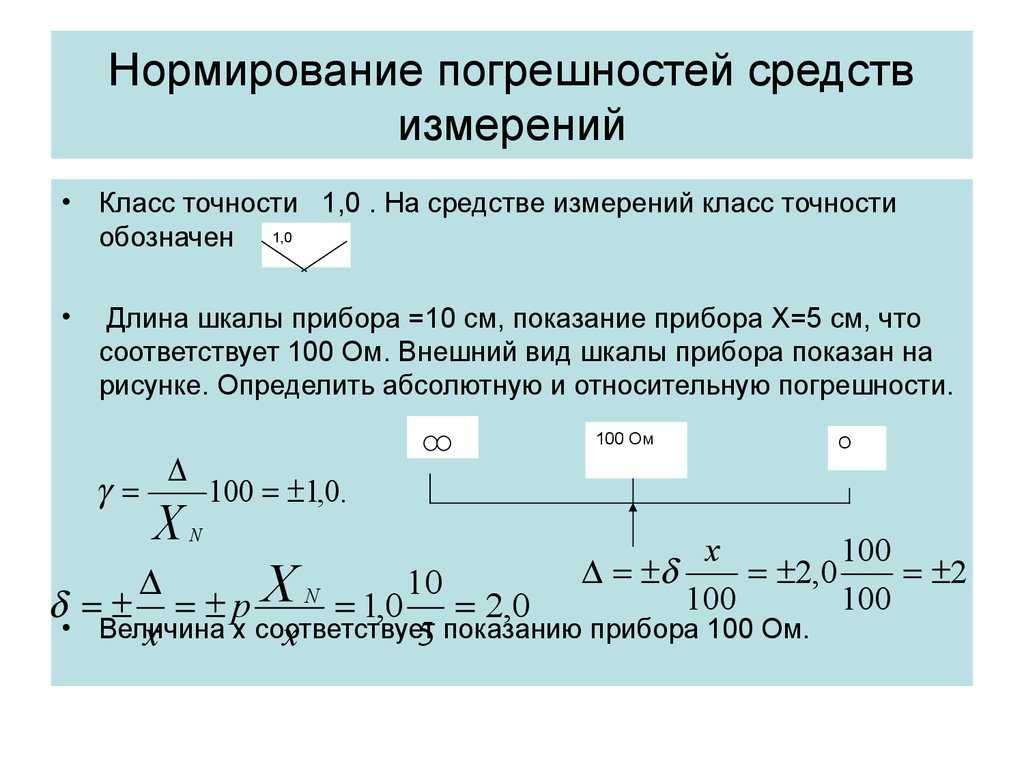
Действительные абсолютные погрешности измерения для каждой пары наблюдений вычислены в табл. 6 при t = 2,2 (М = 16, доверительная вероятность 0,95).
Предельные погрешности измерений для каждой пары наблюдений, вычисленные по формуле (2) настоящего стандарта, приведены в табл. 6. Допуски на разбивку осей в плане определялись по табл. 5 ГОСТ 21779-82 соответственно 6-му классу точности.
Действительные погрешности измерений, в основном, не превышают требуемых. Наблюдения с порядковым номером 4 следует повторить при m = 3 , 4.

Распечатать

Как рассчитать точность измерений

Обновлено 2 ноября 2020 г.

Кевин Бек

Наука в значительной степени основана на количественных данных. Сбор полезных данных, в свою очередь, зависит от некоторых измерений, при этом масса, площадь, объем, скорость и время являются одними из этих критически важных показателей.

Ясно, что точность, которая показывает, насколько точно измеренное значение приближается к своему истинному значению, жизненно важна во всех научных начинаниях. Это верно не только по наиболее очевидным сиюминутным причинам, таким как необходимость знать температуру снаружи, чтобы правильно одеться, но и потому, что неточные измерения сегодня приводят к накоплению неверных данных в долгосрочной перспективе. Если данные о погоде, которые вы собираете прямо сейчас, неверны, климатические данные о 2018 году, которые вы просматриваете в будущем, также будут неверными.

Чтобы определить точность измерения, обычно необходимо знать истинное значение этого измерения. Например, «честная» монета, подброшенная очень большое количество раз, должна выпадать орлом в 50% случаев и решкой в ​​50% случаев на основе теории вероятности. В качестве альтернативы, чем более воспроизводимым является измерение (то есть чем выше его точность ), тем более вероятно, что значение будет близко к реальному значению в природе. Если оценки чьего-либо роста, основанные на показаниях 50 очевидцев, находятся в диапазоне от 5 футов 8 дюймов до 6 футов 0 дюймов, вы можете с большей уверенностью заключить, что рост человека близок к 5 футам 10 дюймов, чем если бы оценки находились в диапазоне от 5 футов 8 дюймов до 6 футов 0 дюймов. от 5 футов 2 дюймов до 6 футов 6 дюймов, несмотря на то, что последний дает то же среднее значение 5 футов 10 дюймов.

Чтобы экспериментально определить точность измерений, необходимо определить их отклонение ​.

Соберите как можно больше измерений того, что вы измеряете

Позвоните по этому номеру ​ N ​. Если вы оцениваете температуру с помощью разных термометров неизвестной точности, используйте как можно больше различных термометров.

Найдите среднее значение ваших измерений

Сложите измерения и разделите на Н ​. Если у вас есть пять термометров и измерения в градусах Фаренгейта составляют 60°, 66°, 61°, 68° и 65°, среднее значение равно

\frac{60 + 66 + 61 + 68 + 65}{5} = \frac {320}{5} = 64°

Найдите абсолютное значение разницы каждого отдельного измерения от среднего

Это дает отклонение каждого измерения. Причина, по которой необходимо абсолютное значение, заключается в том, что некоторые измерения будут меньше истинного значения, а некоторые будут больше; простое сложение необработанных значений даст в сумме ноль и ничего не скажет о процессе измерения.

Найдите среднее значение всех отклонений, сложив их и разделив на N

Полученная статистика предлагает косвенную меру точности ваших измерений. Чем меньшую долю самого измерения представляет собой отклонение, тем больше вероятность того, что ваше измерение будет точным, хотя необходимо знать истинное значение, чтобы быть абсолютно уверенным в этом. Таким образом, если возможно, сравните результат с эталонным значением, например, в данном случае с официальными данными о температуре от Национальной метеорологической службы.

Формула точности — узнайте, как определить точность

Формула точности помогает определить ошибки при измерении значений. Если измеренное значение равно фактическому значению, то говорят, что оно высокоточное и с низкими ошибками. Точность и частота ошибок обратно пропорциональны. Высокая точность означает низкий уровень ошибок, а высокий уровень ошибок означает низкую точность. Формула точности дает точность в процентах, а сумма точности и частоты ошибок равна 100 процентам.

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.

Забронируйте бесплатный пробный урок

Разбивайте сложные понятия с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.

Забронировать бесплатный пробный урок

Что такое формула точности?

Формула точности дает точность как разницу частоты ошибок от 100%. Чтобы найти точность, нам сначала нужно рассчитать частоту ошибок. А частота ошибок — это процентное значение разницы наблюдаемого и фактического значения, деленное на фактическое значение.

Точность = 100 % – частота ошибок 

Частота ошибок  = |Наблюдаемое значение – фактическое значение|/фактическое значение × 100 

Давайте рассмотрим несколько примеров ниже, чтобы лучше понять формулу точности.

1. Пример 1: Длина прямоугольной коробки составляет 1,2 метра, но она была измерена рулеткой, и длина была измерена как 1,22 метра. Найдите точность измерения.

   Решение:

   Учитывая длину прямоугольной коробки = 1,20 метра
   Измеренная длина прямоугольной коробки = 1,22 метра

   \(\begin{align} \text{Коэффициент ошибок}  &= \dfrac{\text{|Измеренное значение – заданное значение|}}{\text{Заданное значение}} \times 100 \\&=\frac{ (1.22 — 1.20)}{1.