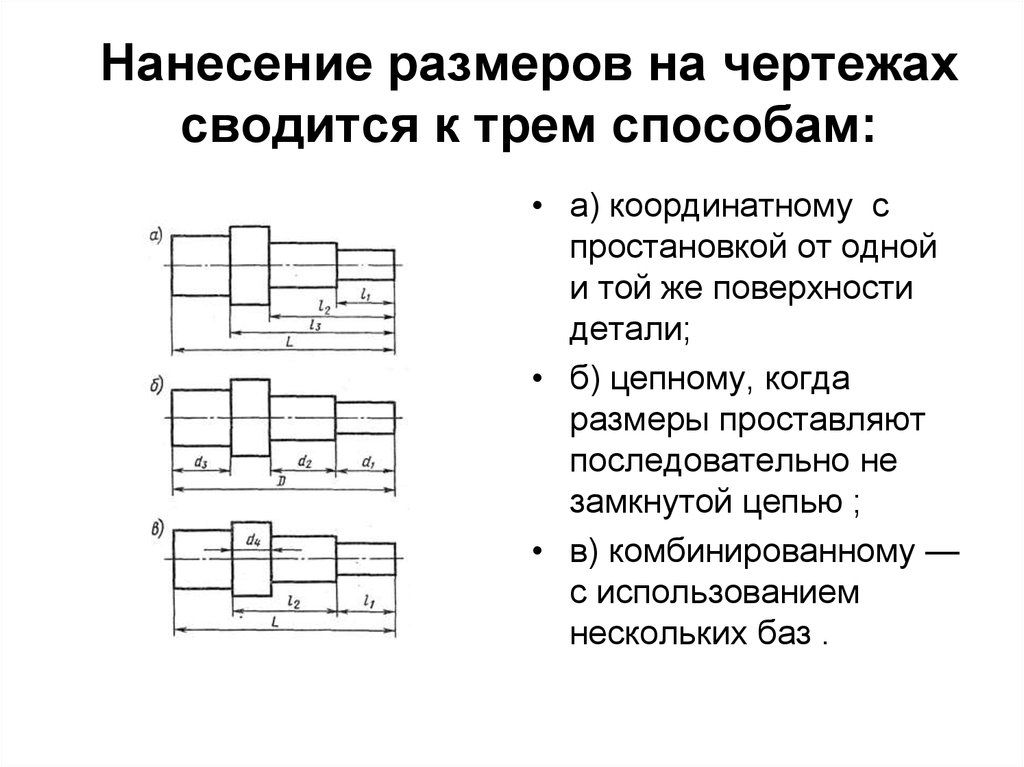
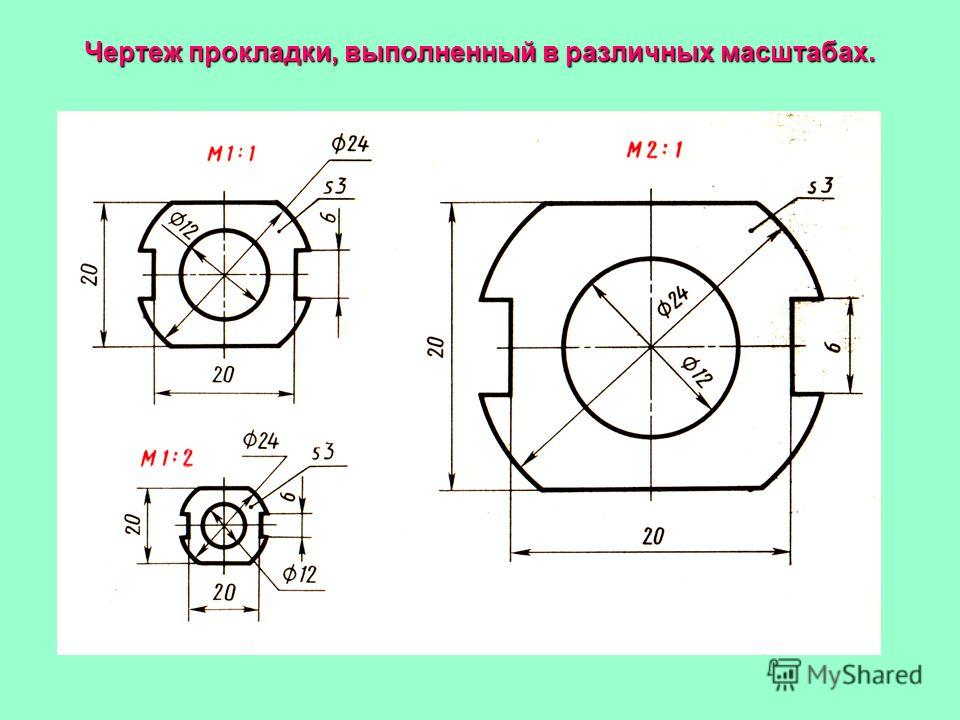
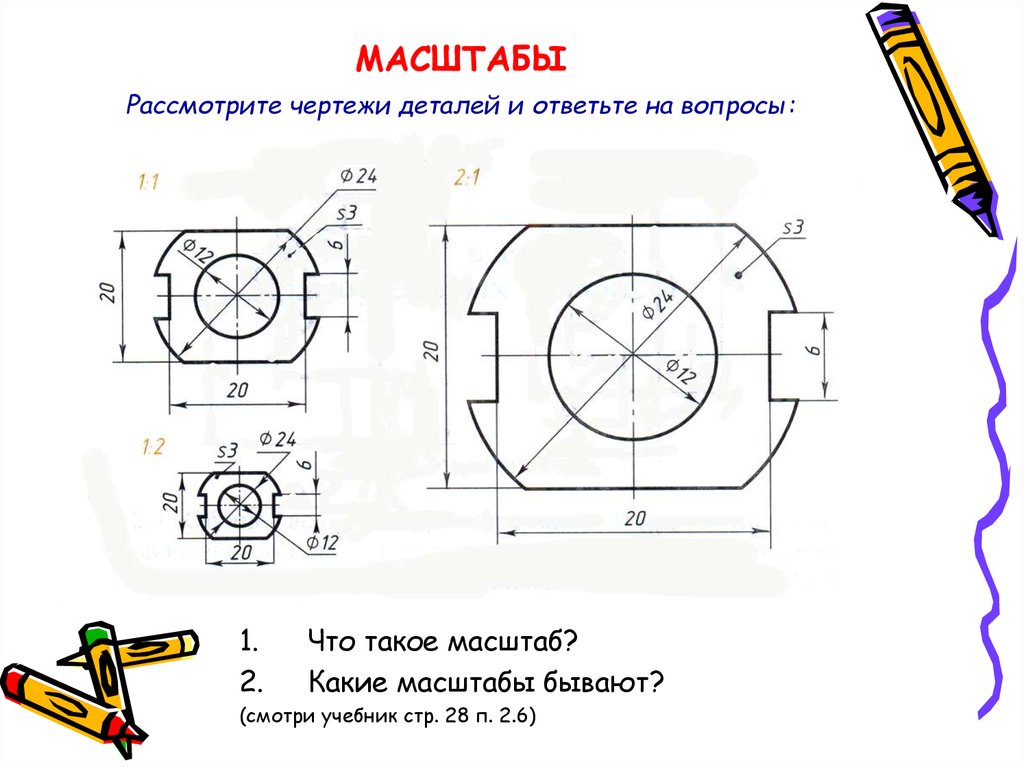
Масштаб черчение: Масштабы чертежей — Чертежик
Содержание
Масштабы чертежей — Чертежик
Масштабы чертежей. Масштабом называется отношение линейных размеров изображения предмета на чертеже к действительным размерам предмета.
Масштабы чертежей бывают численные, линейные, поперечные (десятичные) и угловые (пропорциональные).
Численный масштаб обозначается дробью, которая показываем кратность увеличения или уменьшения размеров изображения на чертеже. Численный масштаб обозначается дробью, которая показываем кратность увеличения или уменьшения размеров изображения на чертеже.
Графические масштабы на чертеже
В зависимости от сложности и величины изображения, ею назначения, стадии проектирования на чертежах применяются:
1.) Масштабы уменьшения: 1:2; 1 :2,5; 1:4; 1 : 5; 1 : 10; 1 : 15; 1:20; 1:25; 1 : 40; 1:50; 1:75; 1: 100; 1:200; 1:400; 1:500; 1:800; 1:1000. (
(
Пример: допустим дана длина 5000 мм. Необходимо начертить в масштабе 1:100, то чертится отрезок размером 50 мм.)
При проектировании генеральных планов крупных объектов допускается применять масштабы: 1:2000; 1:5000; 1: 10000; 1:20000; 1:25000; 1: 50000.
2.) Масштабы увеличения: 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100: 1.
Пример: допустим дана длина 50 мм. Необходимо начертить в масштабе 2:1, то чертится отрезок длиной 100 мм.)
В необходимых случаях допускается применять масштабы увеличения 100-n : I. где n — целое число.
3.) Натуральная величина: 1:1.(пример: длина детали 10 мм.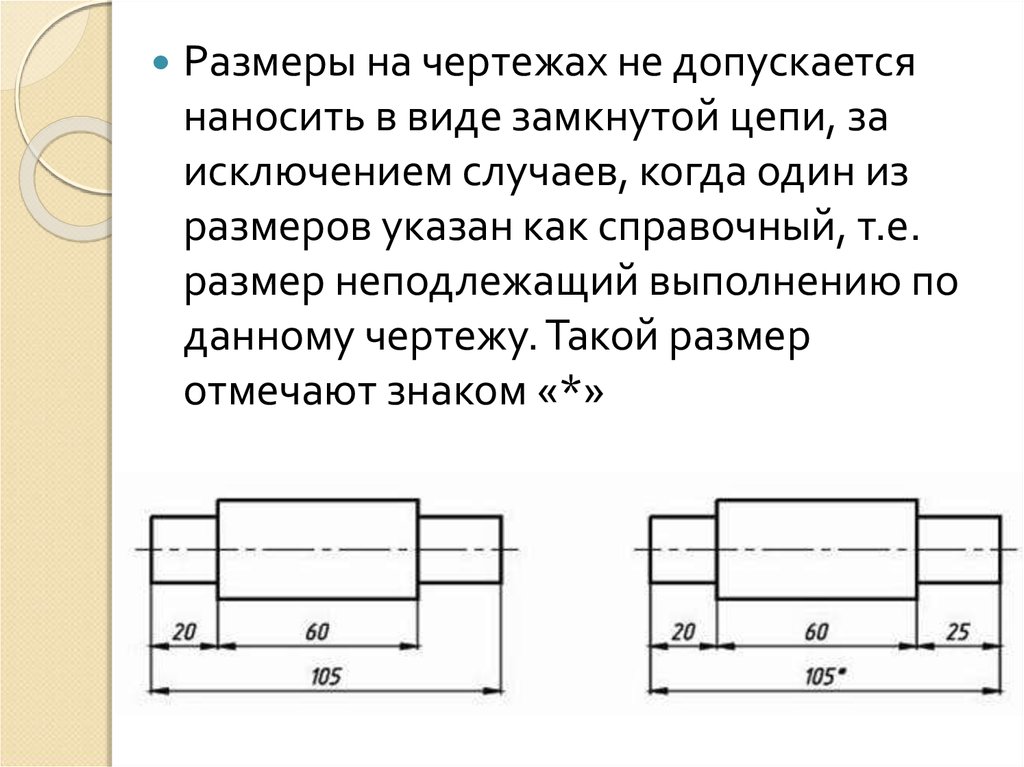 , соответственно, чертим линию размером 10мм. )
, соответственно, чертим линию размером 10мм. )
Масштаб должен указываться на всех чертежах, кроме некоторых строительных, а также чертежей, воспроизводимых путем клиширования или фотографирования.
Если на листе все чертежи выполнены в одном масштабе, то его значение проставляют в соответствующей графе основной надписи по типу 1:1; 1:2; 2:1 и т. д. Если на одном листе помещены чертежи разного масштаба, то масштаб указывают под названием соответствующего чертежа но типу М1:1; М1:2 и т. д.
Линейный масштаб на чертеже имеет вид линии с делениями, означающими какую-нибудь меру длины, например метр, километр и т.п. Линейные масштабы удобны тем, что с их помощью можно без вычисления определять по чертежу действительные размеры. По линейному масштабу отсчет размеров можно про-изводим.
Поперечный масштаб, позволяющий измерять размеры на чертеже с точностью до 0,01 принятой единицы длины, применяется в топографическом черчении.
Угловые (пропорциональные) маштабы применяют для построения изображений в уменьшенном или увеличенном в несколько раз виде.
Угловым масштабом целесообразно пользоваться, когда масштаб чертежа неопределенный 1 : n, где n может быть любое целое или дробное число и при ограниченном количестве размеров на чертеже.
Применение масштабов смотрите в примерах чертежей и в разделе чтение сборочного чертежа
Урок черчения по теме: «Масштабы». 8-й класс
Цели урока.
1. Обобщение знания учащихся по теме.
2. Ознакомление со стандартами масштабов.
3. Научить практическому применению масштабов.
Воспитательные задачи.
1. Воспитывать у учащихся чувство гордости за
вклад русских
изобретателей в развитие чертежа.
2.Формировать навыки самостоятельной работы.
Развивающая задача.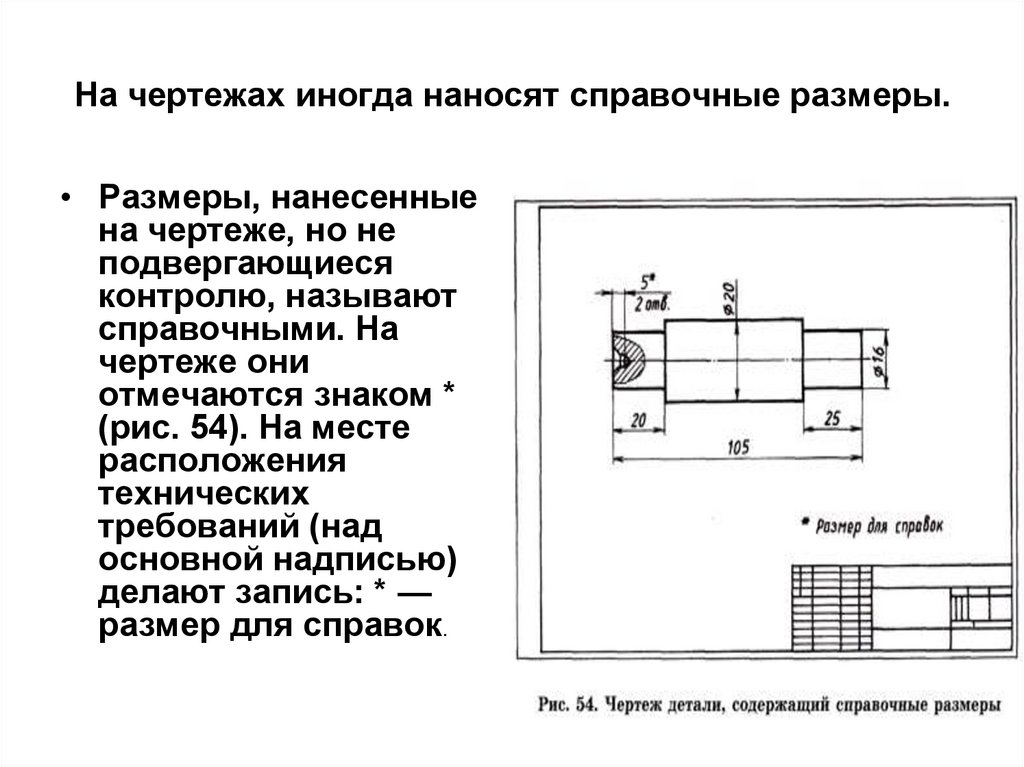 Развивать техническое
Развивать техническое
и образное мышление.
Тип урока. Комбинированный
Пособия и оборудование. Учебные таблицы:
чертеж прокладки, виды масштабов.
Модели прокладок.
Чертежные инструменты, тетради, учебник.
Словарь. Масштаб натуральный, увеличение,
уменьшение, линейный.
Подготовительная работа к уроку.
Учащимся дается задание подготовить материал о
прошлом русского масштабного чертежа.
План урока.
1. Организационный момент.
2. Целеполагание.
3. Актуализация знаний:
3.1 Повторение темы “нанесение размеров”.
3.2 Историческая справка.
3. Обобщение знаний по теме урока.
4. Изучение нового материала.
5. Практическая работа.
6. Домашнее задание.
7. Итог урока.
Ход урока
1.
 Организационный момент
Организационный момент
.
2. Целеполагание:
— повторить правила нанесения размеров на
чертеж;
— совершим небольшое путешествие в прошлое
русского масштабного чертежа;
— обобщим знания по теме урока;
— ознакомимся с ГОСТами на масштабы;
— научимся применять масштаб при построении
чертежа.
3. Актуализация знаний.
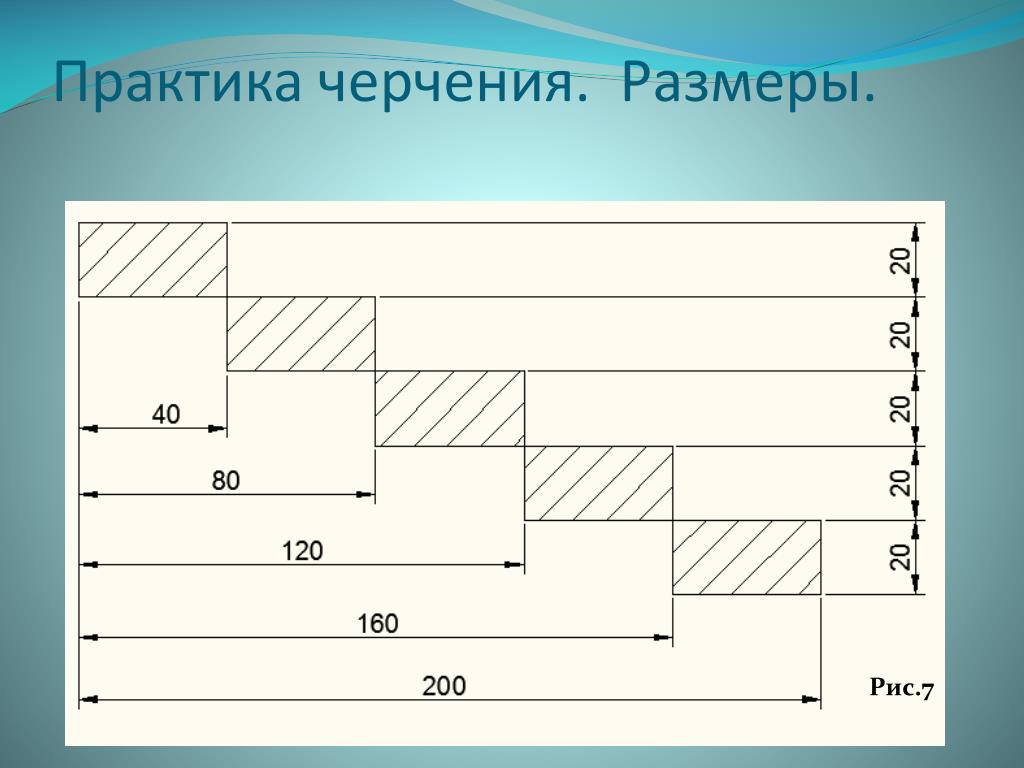
3.1 Повторение по теме “Нанесение размера”.
Задание 1. На доске выполнить <Рисунок
1> и <Рисунок 2>. Работают два
ученика.
Нанести необходимые размеры на заданный
чертеж.
Задание 2. Остальные учащиеся выполняют
самостоятельную работу по индивидуальным
карточкам <Рисунок 3>.
Время работы 5 минут.
Проверка работы учащихся , которые выполнили
задание у доски:
— отчет ученика о выполненной работе;
— высказывание учащихся класса и анализ
допущенных ошибок;
— ответы на дополнительные вопросы .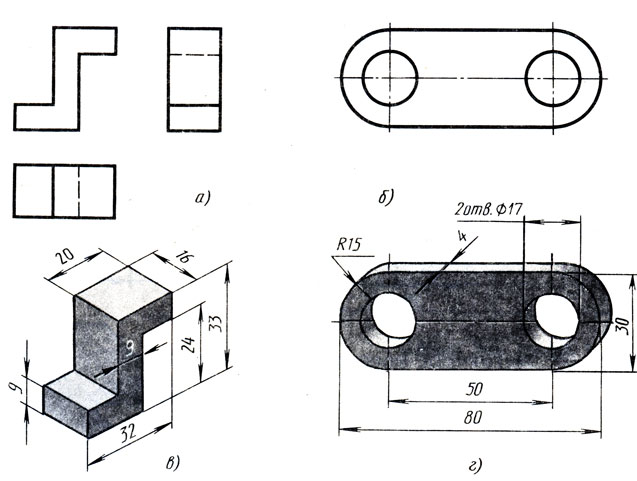
Вопрос 1. На каком расстоянии от контура
чертежа проводят размерную линию?
Вопрос 2. Что означает запись S 3?
Вопрос 3. Какой длины стрелки на размерной
линии?
Вопрос 3. Что означает знак ?
— оценка ЗУМ учащихся.
3.2 Историческая справка.
Сообщения учащихся.
Ученик 1. Первые масштабы на чертежи начали
указывать с XVII века. С введением масштаба резко
увеличилась точность графических построений.
Поэтому в конце XVII века решением Петра 1 в России
были введены масштабные изображения, которые
окончательно утвердились к концу XVIII столетия. В
это время чертежи еще не содержали числовых
размеров и, их определяли путем обмера чертежа с
помощью циркуля-измерителя и линейного или
поперечного масштаба, которые изображались
внизу чертежа <Рисунок 4>.
Учитель. В настоящее время линейные и
В настоящее время линейные и
поперечные масштабы помещаются на
топографических планах и картах в архитектурных
проектах
Ученик 2. В 90-х годах появляется численный
масштаб на машиностроительных чертежах и
обозначался так: “Уменьшен в 1/10 долю”, “ Масштаб
в 1/10 долю”, “ Масштаб 1:10 от н.в.”, где н.в. –
натуральная величина и т.д.
Ученик 3. В 1806 году военному ведомству было
предписано ввести в чертежи числовые размеры.
Теперь “…, не нужно мерить циркулем по масштабу,
а только смотреть на цифры”. С введением
числовых размеров с конца 70-х годов линейные и
поперечные масштабы исчезли с
машиностроительных чертежей.
3.3 Обобщение знаний учащихся по теме
“Масштаб” (в диалоговой форме).
Учитель. С этим словом вы познакомились
на уроках географии и математики, когда
изображали местность на листе бумаги, для этого
выбирали масштаб.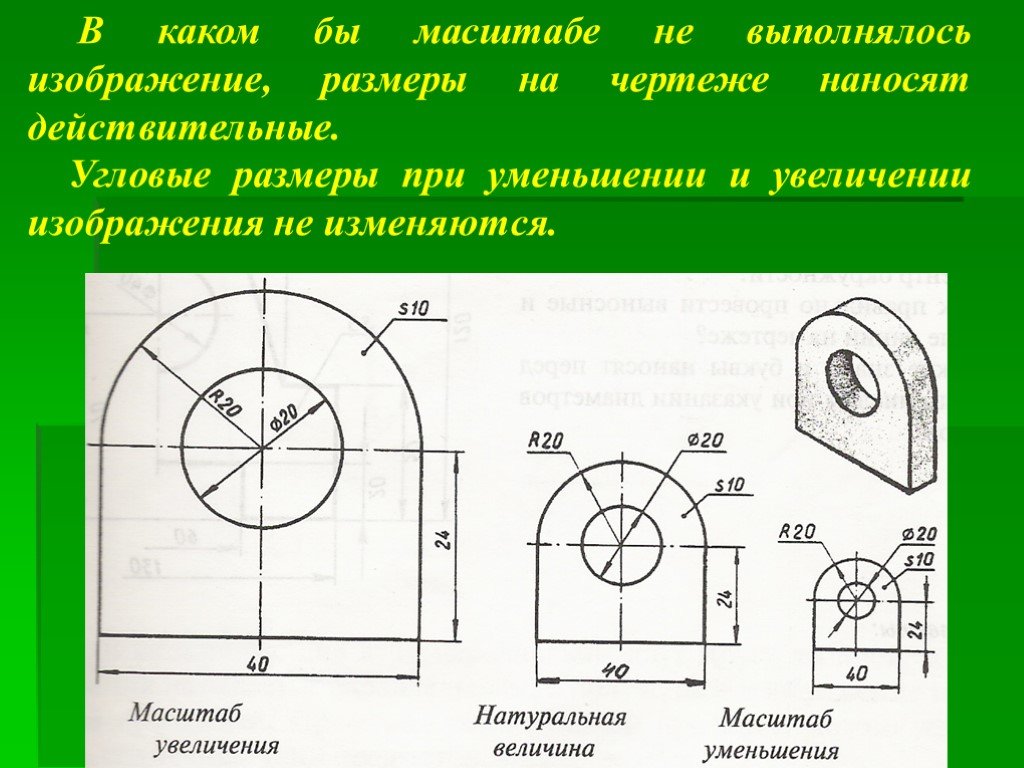 С географической точки зрения,
С географической точки зрения,
что показывает масштаб?.
Ученик Масштаб показывает во сколько раз
расстояние на плане меньше, чем на местности.
Учитель Если масштаб на карте записан 1:1000;
1:200; 1:50, что это означает?
Ученик Запись в таком виде означает, что
это численный масштаб.
Учитель Рядом с численным масштабом пишут
пояснения: в 1 см – 10 м. Как называется этот
масштаб?
Ученик Этот масштаб называют именованным.
Учитель Что означает выражение “Величина
масштаба”?
Ученик Это расстояние в 1 см на плане.
Учитель Для более точного определения
расстояния на плане помещают этот масштаб.
Как его называют?
Ученик Такой масштаб называют линейным.
4.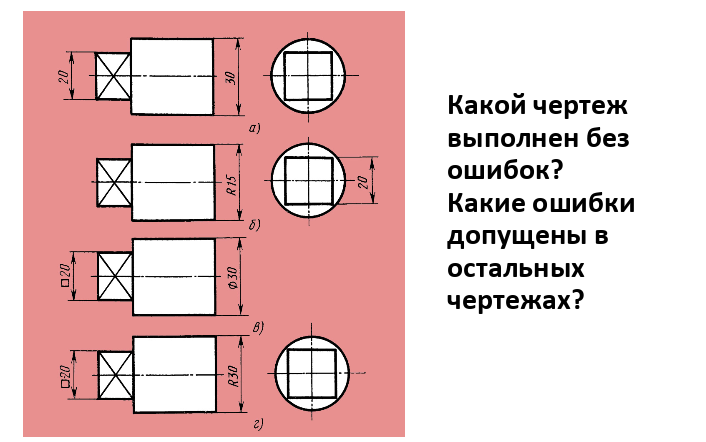 Изучение нового материала
Изучение нового материала
Учитель Очень часто при выполнении
практических работ приходится вычерчивать очень
крупные детали самолетов, кораблей, автомашин,
зданий или очень мелкие детали часового
механизма, точных приборов и т.д..
Учитель демонстрирует две прокладки разной
величины , изготовленные из картона.
Учитель Какие трудности могут возникнуть
при выполнении чертежей этих деталей?
Варианты ответов учащихся:
— большая прокладка не поместится на чертежном
листе.
— вторая прокладка очень мала, и на чертеже
трудно нанести размеры.
Учитель Как вы поступите?
Ученик Большого размера прокладку мы
уменьшим, а меньшую – увеличим.
Учитель Правильно, воспользуемся
масштабом. Масштаб — это отношение размеров
изображения к действительным размерам
изображаемого предмета [3].
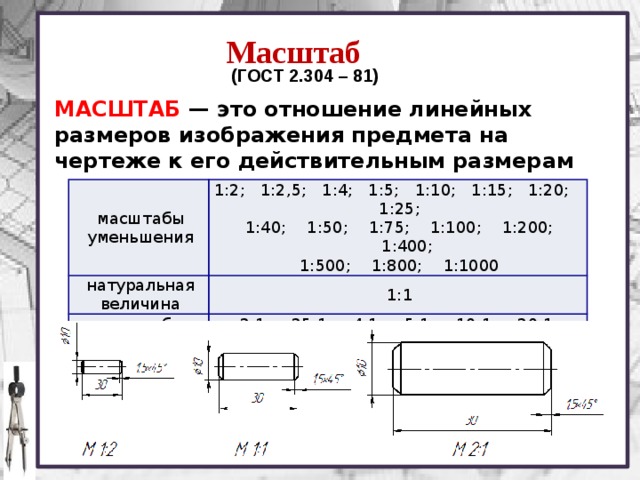
ГОСТ 2.302-68 устанавливает следующие масштабы:
| Действительный масштаб | 1:1 |
| Масштаб увеличения | 2:1; 2,5:1; 4:1; 5:1….100:1 |
| Масштаб уменьшения | 1:2; 1:2,5; 1:5; …1:100 |
5. Применение изученного материала при
выполнении практической работы.
На доске плакаты с чертежом в М 1:1.<Рисунок
5>
Учитель Наша задача построить данный
чертеж в М 2:1 и нанести размеры. Воспользуемся
тем, что деталь имеет только прямые углы, поэтому
работать будем по следующему алгоритму.
Алгоритм.
1. Построить прямой угол в точке К. <Рисунок
6>
2. Измерить отрезок АЕ и отложить его вниз от
точки К два раза, поставить точку П.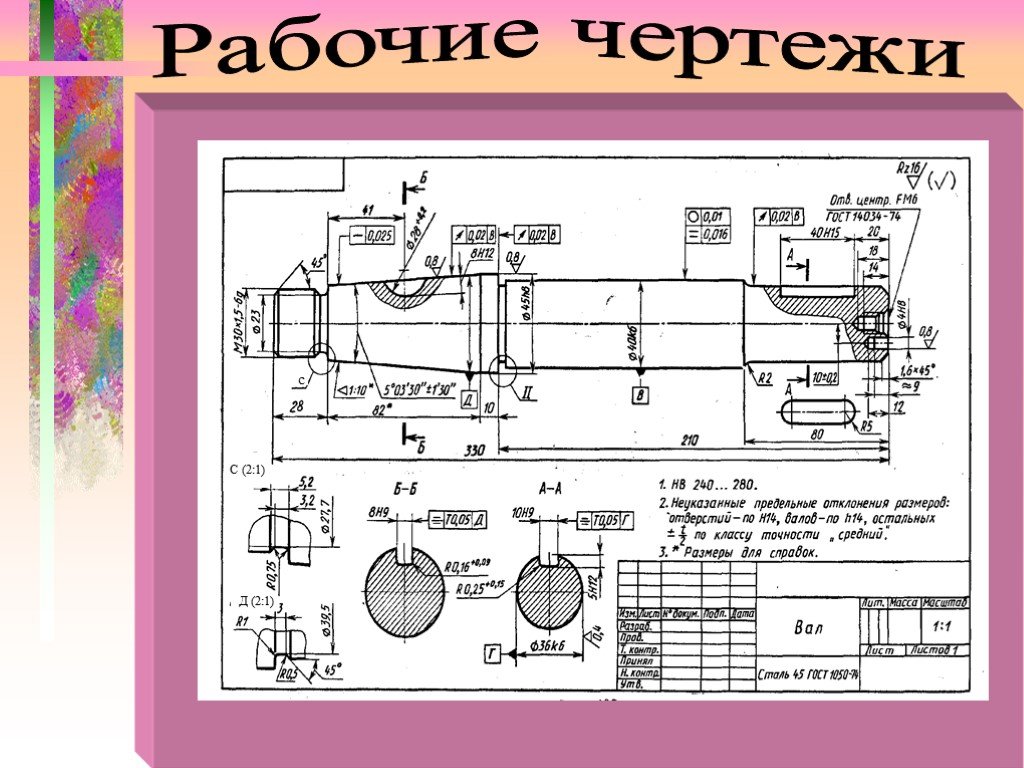
<Рисунок 7>.
3. Измерить отрезок АБ и отложить его от точки К
по горизонтальной линии два раза , поставить
точку Л. <Рисунок 8>
4. В точке П построить прямой угол <Рисунок
9>.
5. Измерить отрезок ЕД и отложить его по стороне
угла два раза, поставить точку О.
<Рисунок 10>.
6. Из точки О восстановить вверх перпендикуляр.
<Рисунок 11>.
7. Измерить расстояние ДГ и отложить его от
точки О вверх два раза , поставить точку Н.
<Рисунок 12>.
8. Из точек Л и Н восстановить перпендикуляры до
пересечения, место пересечения обозначить
М. <Рисунок 13>.
9. Нанести размеры, соблюдая правила. <Рисунок 14>.
Памятка:
При любом масштабе на
|
При построении чертежа пункты алгоритма 5, 6, 7, 8
и 9 учащиеся выполняют самостоятельно.
6. Задание на дом.
Построить чертеж в М1:2, пользуясь чертежом из
тетради М1:1.
Учить Стр. 30-31 [5]
7. Итог урока:
Обобщается :
7. 1. Что узнали нового?
7. 2. Какие практические навыки закрепили.
7. 3. Какие новые практические навыки вы
приобрели.
7. 4. Что удалось на уроке?
7. 5. Над чем еще надо поработать
7.6. Оценить труд учащихся.
ЛИТЕРАТУРА
- Н.Г. Преображенская, Т.В.Кучукова, И.А. Беляева.
Черчение. Рабочая тетрадь №1. основные правила
оформления чертежей. Построение чертежа
“плоской” детали. - В.
 Н. Виноградов. Внеклассная работа по черчению
Н. Виноградов. Внеклассная работа по черчению
в школе. Издание второе, дополненное.
Издательство “Просвещение”.Москва. 1965гю - В.В.Степакова, Л.Н. Анисимова, Л.В. Курцаева, А.И.
Шершевская. Черчение. Учебник для учащихся
общеобразовательных учреждений. Под редакцией
В.В.Степаковой. Допущено Министерством
образования Российской Федерации .Москва
“Просвещение” 2001г. - Черчение учебник для учащихся средних
общеобразовательных учреждений. Под редакцией
проф. Н.Г. Преображенской. Допущено Министерством
образования Российской Федерации. Москва.
Издательский центр “Вентана-Граф” 2002г. - А.Д Ботвинников, В.Н Виноградов, И.С
Вышепольский. Черчение. Учебник для 7-8 классов
общеобразовательных учреждений. Москва,
“Просвещение”. 1997.
7 класс.Москва. Издательский центр
“Вентана-Граф”. 1998.
Чертеж в масштабе — математика GCSE
Введение
Что такое чертеж в масштабе?
Как рассчитать фактическое/реальное жизненное расстояние по шкале
Рабочий лист чертежа в масштабе
Как рассчитать расстояние отрисовки шкалы по шкале
Распространенные заблуждения
Вопросы по рисованию в масштабе
Рисование в масштабе GCSE вопросы
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Что такое чертеж в масштабе?
Как рассчитать фактическое/реальное жизненное расстояние по шкале
Лист чертежа в масштабе
Как рассчитать расстояние отрисовки шкалы по шкале
Распространенные заблуждения
Вопросы по рисованию в масштабе
Рисование в масштабе Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем о чертежах в масштабе, включая создание чертежей в масштабе, использование коэффициентов масштабирования и решение текстовых задач.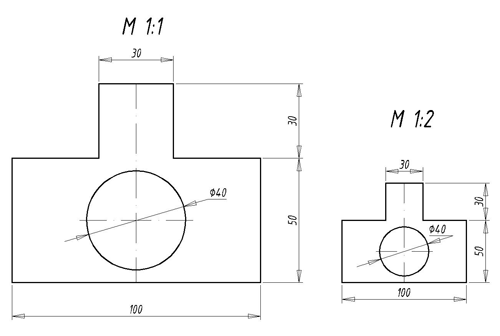
Существуют также масштабные диаграммы и чертежи рабочие листы, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое чертеж в масштабе?
Чертеж в масштабе — это увеличение объекта .
Увеличение изменяет размер объекта путем умножения каждой из длин на масштабный коэффициент , чтобы сделать его на больше или на меньше .
Масштаб чертежа обычно указывается в виде соотношения .
1 см: 5 м
Это называется «от 1 сантиметра до 5 метров» и означает, что каждый 1 сантиметр на диаграмме соответствует 5 метрам в реальной жизни.
Чтобы интерпретировать и создавать чертежи в масштабе, нам необходимо знать масштабный коэффициент и фактическую длину объекта.
Ниже приведен чертеж бассейна в масштабе в масштабе \bf{1cm:2m} или 1:200.
Это означает, что каждый сантиметр на диаграмме соответствует 2 метрам в реальной жизни.
Таким образом, ширина диаграммы 6 см соответствует ширине 12 м в реальном бассейне.
Реальный пул был увеличен с коэффициентом масштабирования \frac{1}{200}, чтобы получить изображение в масштабе.
Большинство вопросов по чертежам в масштабе будут включать многоугольники или 2D-чертежи , такие как планы этажей или использование карты , хотя есть совпадения с такими темами, как расширение, построение треугольников и локусов .
Что такое чертеж в масштабе?
Как рассчитать фактическое/реальное расстояние по шкале
Для расчета фактического/реального расстояния по шкале:
- Масштаб увеличения указать как отношение в форме \ бф{1:n} .

- Умножьте \bf{n} на длину, указанную на чертеже в масштабе.
- Запишите единицы измерения.
Объясните, как рассчитать фактическое / реальное расстояние по шкале
Рабочий лист для рисования в масштабе
Получите бесплатный лист для рисования в масштабе, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКОРО
Икс
Рабочий лист для рисования в масштабе
Получите бесплатный лист для рисования в масштабе, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКОРО
Связанные уроки в масштабе
Чертеж в масштабе является частью нашей серии уроков для поддержки пересмотра в масштабе . Возможно, вам будет полезно начать с основного урока по шкале, чтобы получить общее представление о том, чего ожидать, или использовать пошаговые руководства ниже для получения более подробной информации по отдельным темам.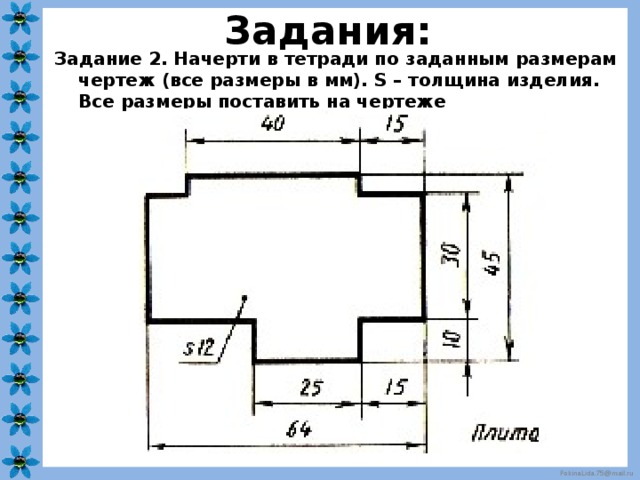 Другие уроки этой серии включают:
Другие уроки этой серии включают:
- Математика в масштабе
- Диаграмма в масштабе
Примеры чертежей в масштабе
Пример 1: карта
Карта имеет масштаб 1см:2км. Найдите фактическое расстояние, представленное 5 см на карте.
- Укажите масштаб увеличения в виде отношения \bf{1:n} .
1 см: 2 км
2 Умножьте \bf{n} на длину, указанную на чертеже в масштабе.
2 х 5=10
3 Запишите единицы измерения.
10км.
Пример 2: план здания
План многоквартирного дома имеет масштаб 2,5см:800м. Какое реальное расстояние представлено на плане 5,7 см?
Укажите масштаб увеличения в виде отношения \bf{1:n} .
Разделив обе стороны на 2,5, получим 1см:320м
Умножьте \bf{n} на длину, указанную на чертеже в масштабе.
320 х 5,7=1 \ 824
Запишите единицы измерения.
1 \ 874м
Пример 3: атлас
Атлас мира имеет масштаб 2см:5\000км. Рассчитайте реальное расстояние, которое в атласе представлено цифрой 23 мм.
Укажите масштаб увеличения в виде отношения \bf{1:n} .
Поскольку необходимая длина указана в миллиметрах, сначала нам нужно изменить 2 см на миллиметры.
2см:5 \ 000км = 20мм:5 \ 000км
Мы можем уменьшить это соотношение так, чтобы у нас было 1 \ мм:n \ км. Разделив обе части на 20, получим:
1 мм:250 км
Умножьте \bf{n} на длину, указанную на чертеже в масштабе.
250 х 2,3=575
Запишите единицы измерения.
575км
Как рассчитать дальность прорисовки шкалы по шкале
Чтобы рассчитать дальность прорисовки шкалы по шкале:
- Масштаб увеличения указать в виде отношения в виде 2 \bf{1:n} .

- Разделите реальное расстояние на коэффициент масштаба.
- Запишите единицы измерения.
Примеры расчета расстояния чертежа в масштабе
Пример 4: модель объекта
Модель автомобиля изготовлена с использованием модели с фактическим расстоянием 1см:40см. Высота машины 170см. Рассчитайте высоту модели автомобиля.
Укажите масштаб увеличения в виде отношения в форме \bf{1:n} .
Полученное соотношение равно 1:40
Разделите реальное расстояние на коэффициент масштаба.
170 \дел 40=4,25
Запишите единицы измерения.
4,25 см
Пример 5: план этажа
На плане кухни используется масштаб 1 см:0,2 м. Рассчитайте расстояние на плане для фактического расстояния 5,62 м.
Укажите масштаб увеличения в виде отношения в форме \bf{1:n} .
Соотношение уже в форме 1:n.
1см:0,2м
Разделите реальное расстояние на коэффициент масштаба.
5,62 \дел 0,2=28,1
Запишите единицы измерения.
28,1см
Пример 6: карта Великобритании
Карта Великобритании нарисована в масштабе 50см:1400км. Подсчитайте, как далеко будет 86,8 км на карте.
Укажите масштаб увеличения в виде отношения в форме \bf{1:n} .
Преобразуем отношение к виду 1 \ см:n \ км, разделив обе части соотношения на 50.
50см:1400км=1см:28км .
Теперь мы можем вычислить длину на карте
86,8 \дел 28=3,1
Запишите единицы измерения.
3,1 см
Распространенные заблуждения
- Умножение реального расстояния на шкалу отношений
Реальное расстояние умножается на шкалу отношений, что дает неверное расстояние на плане.
- Разделение расстояния модели/плана/карты на шкалу отношений
Расстояние на модели/плане/карте делится на шкалу отношений, что означает, что реальное расстояние неверно.
- Неупрощенная шкала отношений
Если задано соотношение 2см:5км, легче вычислить, когда отношение находится в форме 1:n, поэтому мы должны найти эквивалентное соотношение перед использованием шкалы.
Здесь соотношение будет 1 см: 2,5 км, поэтому 1 см на карте будет равен 2,5 км в реальной жизни.
- Неверные единицы измерения в решении
Единицы модели перепутаны с единицами реального расстояния. Например, если бы мы рассчитывали расстояние 10 см на карте с соотношением масштаба 1 см: 5 км, было бы указано \ 10 \ × 5 = 50 см, тогда как правильным решением было бы 10 × 5 = 50 км.
- Блоки преобразования
Иногда единицы измерения необходимо преобразовать, чтобы вы работали с теми же единицами измерения, что значительно упрощает понимание вычислений. Убедитесь, что вы знаете, как конвертировать между различными метрическими единицами. Например, масштаб карты указан как 1:25 000, что означает, что 1 см на карте эквивалентен 25 000 см в реальной жизни.
Убедитесь, что вы знаете, как конвертировать между различными метрическими единицами. Например, масштаб карты указан как 1:25 000, что означает, что 1 см на карте эквивалентен 25 000 см в реальной жизни.
Если ответ просят записать в километрах, то реальное значение в сантиметрах нужно разделить на 100\000, чтобы получить такое же измерение в километрах. 1:25\000 = 1см:0,25км
Practice scale drawing questions
0.86km
0.86cm
10.5km
10.5cm
3 \times 3.5=10.5km
3750km
7500km
33.3km
3750cm
\begin{aligned }
&2см:500км = 1см:250км \\\\
&250\умножить на 15=3750км
\end{выровнено}
10,738 м
10,738 см
107,38 м
\begin{выровнено}
& 1 см: 1,82 м \\\\
&1,82 \умножить на 5,9=10,738 км
\end{выровнено}
0,38864 см
0,38864 м
4,96 см
\begin{выровнено}
&138,8 см=1,388 м \\\\
& 10 см: 2,8 м = 1 см: 0,28 м \\\\
&1,388 \дел 0,28=4,96 см
\end{выровнено}
1,061 м
13,26 м
10,61 м
1,326 м
\begin{выровнено}
&8м:1400км=1м:175км \\\\
&175 \дел 132=1,326 м \ (3 дп)
\end{выровнено}
6,22 см
25,2 см
0,9 см: 20 см = 1 см: 22. \ точка {2} см
\ точка {2} см
Следовательно, отношение модели к реальному составляет 1 см:22.\dot{2}см
\begin{выровнено}
&5.6м=560см \\\\
&560 \div 22. \dot{2}=25,2 см
\end{выровнено}
Чертеж в масштабе Вопросы GCSE
1. Карта имеет масштаб 1 см:0,5 км. Собачник проходит около 18 км в день. Подсчитайте, какое расстояние они пройдут по карте.
(2 балла)
Показать ответ
18 \дел 0,5
(1)
=36см
(1)
2. (a) Расстояние между двумя городами в американском штате составляет 146,8 км. Расстояние между двумя городами на карте составляет 29,36 см. Рассчитайте отношение масштаба карты к фактическому расстоянию в виде 1 см: км.
(b) Длина реки, протекающей через штат, на плане составляет 45 см. Вычислите фактическую длину реки. Укажите единицы измерения в вашем решении.
(4 балла)
Показать ответ
(а)
146,8 \дел 29,36=
(1)
1 см: 5 км
(1)
(б)
45 х 5=225
(1)
км
(1)
3. Ниже представлена карта необитаемого острова.
Используя предоставленный масштаб, рассчитайте расстояние между пальмами и водопадом.
(3 балла)
Показать ответ
Расстояние [6,3-6,7 см]
(1)
Их 6,5 х 50
(1)
325м
(1)
Учебный контрольный список
Теперь вы научились:
- Умножать и делить на 10 на чертежах в масштабе или умножать и делить на 1000 при преобразовании таких единиц, как километры и метры
- Решение задач с похожими формами, когда масштабный коэффициент известен или может быть найден
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.
Чертежи в масштабе
Карта не может быть того же размера, что и область, которую она представляет. Итак
измерения уменьшены до , чтобы сделать карту такого размера, который может быть
удобно использовать такие пользователи, как автомобилисты, велосипедисты и
бушволкеры. Чертеж здания (или моста) в масштабе имеет то же самое.
форму реального здания (или моста), которое оно представляет, но отличается
размер. Строители используют чертежи в масштабе для создания зданий и мостов.
Соотношение используется в масштабных чертежах карт и зданий. То есть:
Аналогично имеем:
Масштаб обычно выражается одним из двух способов:
- в единицах от 1 см до 1 км
- без явного указания единиц измерения, как в 1 : 100 000.

Примечание:
Масштаб 1 : 100 000 означает, что реальное расстояние в 100 000 раз больше
длина 1 ед. по карте или чертежу.
Пример 14
Запишите масштаб от 1 см до 1 м в форме отношения.
Решение:
Пример 15
Упрощение масштаба 5 мм : 1 м.
Решение:
Пример 16
Упрощение масштаба 5 см : 2 км.
Решение:
Расчет фактического расстояния с использованием шкалы
Если масштаб 1 : x , то умножьте расстояние карты на x , чтобы рассчитать фактическое расстояние.
Пример 17
Определенная карта имеет масштаб 1 : 5000.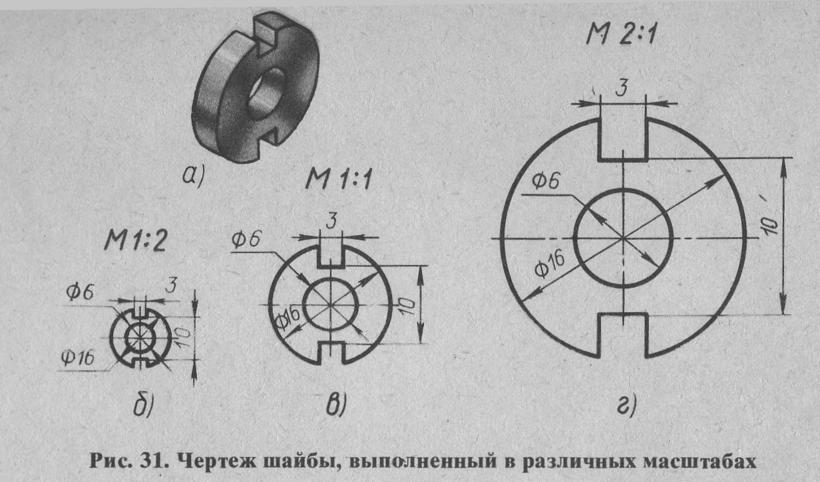
расстояние, если расстояние карты составляет 8 см?
Решение:
Расстояние карты = 8 см
Пусть фактическое расстояние будет см.
Альтернативный способ:
Расстояние карты = 8 см
Расчет масштабированного расстояния с использованием фактического расстояния
Если масштаб 1 : x , затем разделите фактическое расстояние на x , чтобы вычислить расстояние по карте.
Пример 18
На конкретной карте показан масштаб 1 см : 5 км. Что бы карта
расстояние (в см) быть, если фактическое расстояние составляет 14 км?
Решение:
Итак, расстояние карты равно 2,8 см.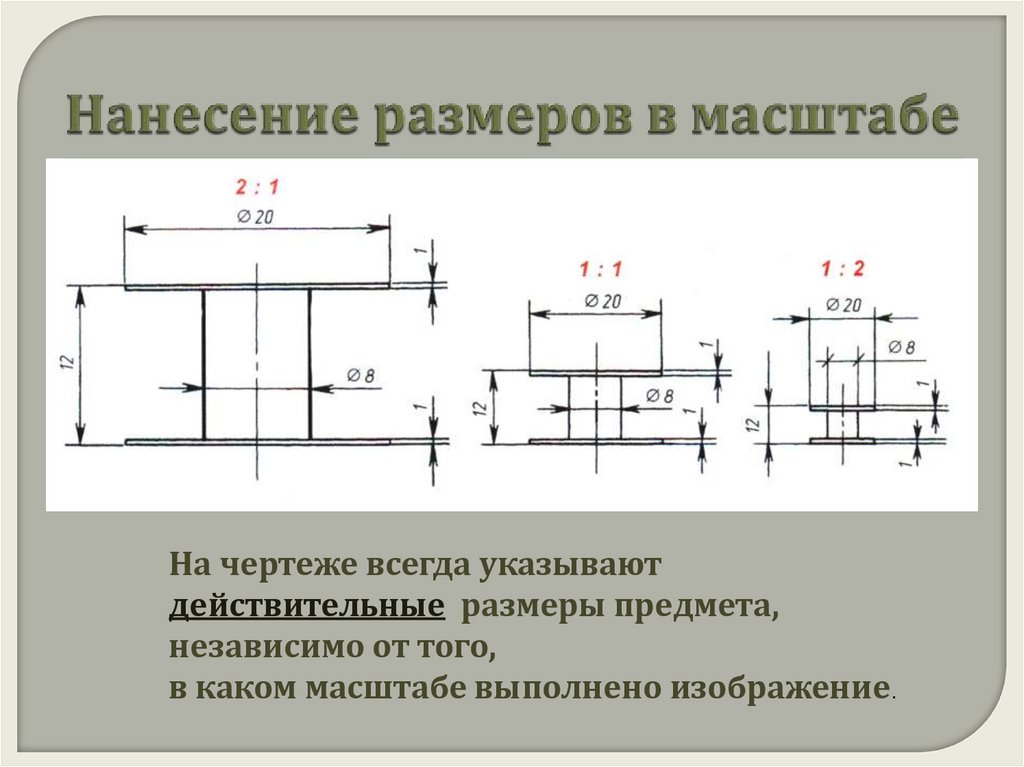
 Н. Виноградов. Внеклассная работа по черчению
Н. Виноградов. Внеклассная работа по черчению