Сечение какой буквой обозначается: Сечение процесса • Физика элементарных частиц • LHC на «Элементах»

Сечение процесса • Физика элементарных частиц • LHC на «Элементах»

Что такое сечение процесса

Когда быстрая частица налетает на частицу-мишень, то для того, чтобы произошло столкновение, она должна пролететь в достаточной близости от мишени, то есть она должна попасть в некоторое поперечное сечение. Эту поперечную площадь и называют в физике эффективным сечением процесса (сечением столкновения, сечением реакции и т. п.).

В классической механике (например, при рассеянии точечных частиц на мишени определенного размера) эффективное сечение равняется просто геометрической площади поперечного сечения мишени. В квантовой механике ситуация меняется, во-первых, из-за волновой природы частиц, а во-вторых, из-за того, что частицы обычно «полупрозрачны» друг для друга (это зависит от типа взаимодействия между частицами). Поэтому эффективное сечение процесса отличается от геометрического сечения.

На иллюстрации схематично показано то, как протон «выглядит» с точки зрения налетающей частицы: второго протона, фотона или нейтрино. Налетающий протон чувствует цельное кварковое и глюонное облако протона-мишени, поэтому сечение протон-протонного столкновения того же порядка, что и геометрическое сечение протона. Фотон чувствует только кварковое распределение, и к тому же сила электромагнитного взаимодействия меньше, чем сильного. В результате протон для фотона кажется полупрозрачным, и эффективное сечение получается заметно меньше. Наконец, нейтрино чувствует не сами по себе кварки, а как бы маленькое облачко виртуальных W- и Z-бозонов вокруг них. Из-за этого протон выглядит для нейтрино почти прозрачным, и эффективное сечение рассеяния нейтрино на протоне очень мало.

Впрочем, в ядерной физике встречаются примеры, когда эффективное сечение процесса заметно больше, чем геометрическое сечение ядра. Например, сечение захвата медленного нейтрона ядром бора-10 превышает геометрическое сечение ядра в десятки тысяч раз. Большое сечение захвата этим изотопом бора используется в бор-нейтронозахватной терапии раковых опухолей.

Более детальную информацию о внутреннем устройстве частиц можно получить с помощью дифференциального сечения процесса. Дифференциальное сечение — это, условно говоря, площадка, в которую надо попасть, чтобы рожденные частицы вылетели под определенным углом к оси столкновения или с определенным поперечным импульсом.

Единицы измерения

Сечение (обозначается буквой σ), как и всякая площадь, измеряется в квадратных метрах. Для выражения сечений столкновений элементарных частиц используют более удобную единицу — барн (b). 1 b = 10^–24 см² = 10^–28 м². В этих единицах 1 фм² (1 кв. фемтометр, то есть (1 × 10^–15 м)²) равен 10 миллибарн (10 mb). Чем меньше сечение процесса, тем реже он происходит. Наиболее редкие процессы, зарегистрированные на коллайдерах, имеют сечение в доли пикобарна (1 pb = 10^–12 b). Сечение рассеяния солнечных нейтрино составляет порядка 10^–21–10^–18 b в зависимости от энергии нейтрино.

Дополнительная литература:

• Статья Сечение реакции из учебного пособия «Частицы и ядра. Эксперимент». Издательство МГУ, 2005.

Поперечное сечение

Поперечным сечением называется фигура, образованная пересечением продолговатого тела с воображаемой плоскостью, расположенных перпендикулярно друг другу, т.е. когда тело рассекается строго поперек его длины.

Сечение может иметь простую или сложную форму, а также быть составным.

Площадь и размеры (длина и ширина) поперечного сечения равны соответствующим размерам этой фигуры.

Площадь поперечного сечения

В общем случае, площадь поперечного сечения имеющая сложную или составную форму определяется как сумма (иногда с вычитанием) составляющих ее простых фигур, таких как прямоугольник, треугольник и круг.

Формулы для расчета площади основных фигур.

Пример:
Рассчитать площадь поперечного сечения сложной формы с квадратным отверстием и закруглением.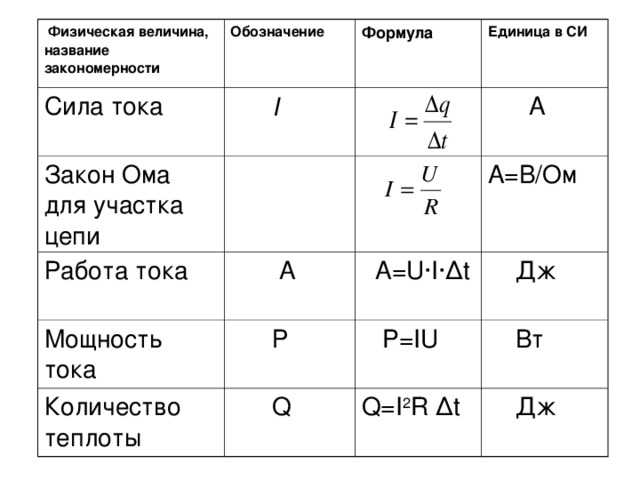

Для расчета общей площади, сложное сечение раскладывается на простые фигуры:

Прямоугольник — 1, треугольник — 2, полукруг — 3 и прямоугольник — 4, площади которых определяются просто.

В итоге площадь всего поперечного сечения будет получена сложением первых трех фигур с вычитанием фигуры номер 4:

A=A₁+A₂+A₃-A₄

Площадь поперечного сечения обозначается латинскими буквами S или A, и измеряется в квадратных единицах длины, например: м², см² или мм².

Площадь составного сечения

Составными называют сечения, которые состоят из двух, трех и более отдельных фигур, не являющихся одним целым.

Это может быть, например сечение балки, состоящее например из швеллера и двух уголков.

Эти сечения сами по себе тоже являются сложными.
Площади поперечного сечения для таких стандартных профилей можно найти в специальном справочнике — сортаменте.

В результате сложив все составляющие профили, получим площадь всего сечения.

Таким образом, расчет площади составного сечения производится аналогично предыдущему порядку, только без вычитаний.

Длина поперечного сечения

Длиной поперечного сечения называют полную (габаритную) длину фигуры как расстояние по горизонтали между двумя её наиболее удаленными точками.

Длина поперечного сечения обозначается латинской буквой L или l и измеряется стандартно в миллиметрах или сантиметрах.

Ширина сечения определяется аналогично, но обозначается буквой H или h.

При решении задач, длину, ширину и площади поперечного сечения рекомендуется переводить соответственно в метры и м².

Понятие «поперечное сечение» является одним из основных при расчетах на прочность в сопротивлении материалов и технической механике.

Различают два основных вида расчета площади сечений:

1. Геометрический — когда требуется найти площадь сечения тела по известным размерам;
2. Прочностной — расчет площади поперечного сечения бруса проводится по условию прочности.

Пример расчета поперечных сечений >

Сохранить или поделиться с друзьями

Вы находитесь тут:

Уважаемые студенты!

На нашем сайте можно получить помощь по техническим и другим предметам:

✔ Решение задач и контрольных

✔ Выполнение учебных работ

✔ Помощь на экзаменах

Подробнее

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Сохранить или поделиться с друзьями

Помощь с решением

ВЫБЕРИТЕ РАЗДЕЛ МЕХАНИКИ

• Техническая механика (техмех)
• Теоретическая механика (теормех)
• Сопротивление материалов (сопромат)
• Строительная механика (строймех)
• Теория механизмов и машин (ТММ)
• Детали машин и ОК (ДМ)

Поиск формул и решений задач

Говорите по физике: Что такое поперечное сечение?

Представьте, что два бильярдных шара катятся навстречу друг другу. Вероятность столкновения зависит от простых для понимания понятий: насколько они велики? Как именно они нацелены?

Когда вы начинаете говорить о вероятности столкновения частиц, все становится сложнее. Вот почему физики используют термин «поперечное сечение».

В отличие от твердых тел элементарные частицы сами ведут себя как крошечные волны вероятности.

И их взаимодействие не ограничивается физическим ударом. Частицы могут взаимодействовать на расстоянии, например, посредством электромагнитной силы или гравитации. Некоторые частицы, такие как нейтрино, лишь изредка взаимодействуют посредством слабого взаимодействия. Вы можете представить их как голограммы бильярдных шаров, которые время от времени переходят в твердое состояние.

Упругая реакция

В физике сечение описывает вероятность взаимодействия двух частиц при определенных условиях. Эти условия включают, например, количество частиц в луче, угол, под которым они попадают в цель, и то, из чего сделана цель.

«Поперечные сечения связывают теорию с реальностью», — говорит Херардо Эррера, научный сотрудник Центра исследований и перспективных исследований Национального политехнического института в Мехико и участник эксперимента ALICE на Большом адронном коллайдере. «Они дают представление о фундаментальных свойствах частиц. В этом их величайшая польза».

Поперечные сечения бывают разных видов. Они могут помочь описать, что происходит, когда частица сталкивается с ядром. В упругих реакциях частицы отскакивают друг от друга, но сохраняют свою идентичность, как два рикошетирующих бильярдных шара. В неупругих реакциях одна или несколько частиц разлетаются на части, как бильярдный шар, пораженный пулей. В резонансном состоянии появляются короткоживущие виртуальные частицы.

Неупругая реакция

Эти измерения одного или нескольких аспектов взаимодействия называются дифференциальными сечениями, а совокупность всех этих реакций, вместе взятых, называется полными сечениями.

Физики представляют сечения в уравнениях с помощью греческой буквы сигма (σ). Но как только они были измерены в реальных столкновениях, их данные можно визуализировать в виде таких цифр:

Этот график взят из статьи о взаимодействиях между нейтрино и атомными ядрами. Вертикальная ось представляет вероятность различных реакций (измеряется в квадратных сантиметрах на гигаэлектронвольты), а горизонтальная ось представляет энергию прилетающих нейтрино (измеряется в гигаэлектронвольтах). Электронвольт — это мера энергии, основанная на количестве энергии, которую получает электрон после ускорения 1 вольтом электричества.

Изображение выше говорит нам, например, что при энергии 10 гигаэлектронвольт наиболее вероятным результатом будет глубокое неупругое рассеяние (зеленая линия), за которым следует резонансное состояние (красная линия) и, наконец, квазиупругое событие (синяя линия). Черная кривая представляет полное поперечное сечение. Столбики погрешностей (тонкие линии, идущие вбок и вверх ногами) указывают предполагаемую точность каждого измерения.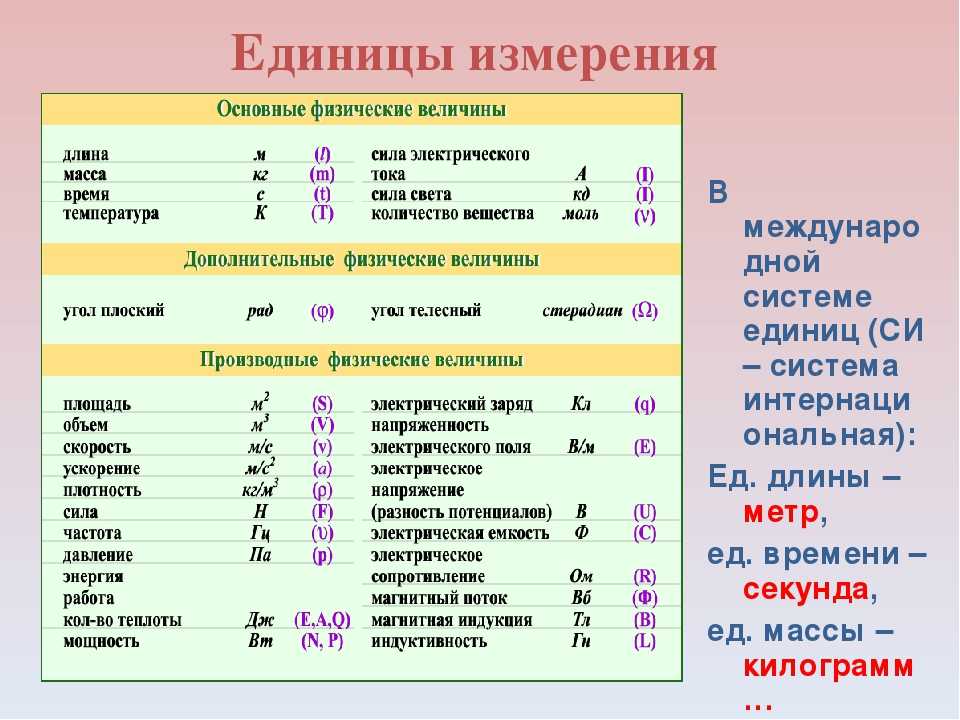

«То, что вы видите на этом рисунке, — это попытки найти общий способ отображения сложных экспериментальных результатов. Этот график показывает, как мы разделяем события, которые находим в наших детекторах», — говорит Хорхе Морфин, старший научный сотрудник Fermilab и один из основных авторов статьи.

Поперечные срезы используются для обмена результатами среди исследователей с общими интересами, говорит Морфин. Таким образом, предыдущее поперечное сечение служит способом сравнения данных, полученных из лабораторий, которые используют разные методы измерения и ядерные цели, таких как NOMAD (CERN), SciBooNE (Fermilab) и T2K (Япония).

Ученые, изучающие астрофизику, квантовую хромодинамику, физическую химию и даже нанонауку, используют такие графики, чтобы понять, как частицы распадаются, поглощают энергию и взаимодействуют друг с другом.

Резонансное состояние

«Они имеют так много связей с различными научными областями и текущими исследованиями», — говорит Том Абель, космолог-вычислитель из Национальной ускорительной лаборатории SLAC и Стэнфордского университета.

Например, в поисках темной материи исследователи выясняют, взаимодействуют ли частицы так, как предсказывают теоретики.

«Мы ищем взаимодействия между частицами темной материи и тяжелыми ядрами или частицы темной материи, взаимодействующие друг с другом», — говорит Абель. «Все это выражается в поперечных сечениях».

Если они видят взаимодействия, отличные от ожидаемых, это может быть признаком влияния чего-то невидимого, например темной материи.

В мире, где правят вероятность и неопределенность, Эррера отмечает, что концепции квантовой механики могут быть трудны для понимания. «Но сечения — это очень осязаемый элемент, — говорит он, — и одно из самых важных измерений в физике высоких энергий».

Механика материалов: кручение » Механика гибких конструкций

исследования

люди

курсы

блог

Деформация при кручении

Крутящий момент — это момент, который скручивает конструкцию. В отличие от осевых нагрузок, которые создают равномерное или среднее напряжение по поперечному сечению объекта, крутящий момент создает распределение напряжения по поперечному сечению. Для простоты мы сосредоточимся на конструкциях с круглым поперечным сечением, часто называемых стержнями или валами. При приложении к конструкции крутящего момента она будет закручиваться вдоль длинной оси стержня, а ее поперечное сечение остается круглым.

Чтобы наглядно представить, о чем я говорю, представьте, что поперечное сечение стержня представляет собой часы с часовой стрелкой. Когда крутящий момент не применяется, часовая стрелка находится в положении 12 часов. Когда к стержню приложен крутящий момент, он будет вращаться, и часовая стрелка повернется по часовой стрелке в новое положение (скажем, на 2 часа). Угол между 2 и 12 часами называется углом поворота и обычно обозначается греческим символом фи . Этот угол позволяет определить сдвиговую деформацию в любой точке поперечного сечения.

Прежде чем мы углубимся в детали этого уравнения, важно отметить, что, поскольку мы обсуждаем только круглых сечений , мы переключились с декартовых координат на цилиндрические координаты. Отсюда и греческий символ rho — он обозначает расстояние по поперечному сечению, где rho=0 в центре и rho=c на внешнем краю стержня.

Из этого уравнения мы можем сразу узнать несколько вещей. Первое может быть очевидным: чем больше угол закручивания, тем больше деформация сдвига (обозначается греческим символом 9).0065 гамма , как и раньше). Во-вторых, и в этом большая разница между конструкциями с осевой нагрузкой и конструкциями с крутящим моментом, деформация сдвига неравномерна по поперечному сечению. Он равен нулю в центре скрученного стержня и имеет максимальное значение на краю стержня. Наконец, чем длиннее стержень, тем меньше деформация сдвига.

До сих пор мы сосредоточили наше внимание на смещениях и напряжениях. Чтобы обсудить напряжение в скрученном стержне, нам нужно знать, как крутящий момент и стресс относятся. Так как скручивание создает сдвиговую деформацию, мы ожидаем, что крутящий момент приложит сдвиговое напряжение . Связь между крутящим моментом и напряжением сдвига подробно описана в разделе 5.2 вашего учебника и приводит к следующему соотношению:

В этом уравнении J обозначает секундный полярный момент площади поперечного сечения. Это иногда называют «вторым моментом инерции», но поскольку это уже имеет устоявшееся значение в отношении динамического движения объектов, давайте не будем путать вещи здесь. Мы обсудим моменты площади более подробно позже, но они принимают очень простую форму для круглых сечений:

(Примечание: это одно и то же уравнение — твердые стержни имеют внутренний радиус c _i = 0).

Теперь у нас есть уравнения для нашей деформации сдвига и напряжения сдвига, все, что осталось сделать, это использовать закон Гука в сдвиге, чтобы увидеть, как они связаны. Закон Гука позволяет нам записать красивое уравнение для угла закручивания – очень удобная вещь для измерения в лаборатории или в полевых условиях.

И точно так же, как мы видели для осевых смещений , мы можем использовать суперпозицию для наших деформации сдвига а также:

Это окончательное уравнение позволяет нам разделить крутящие моменты, приложенные к разным частям одной и той же конструкции. Давайте решим задачу и посмотрим, понимаем ли мы, что происходит с деформациями кручения.

Трансмиссия

Одним из наиболее распространенных примеров кручения в машиностроении является мощность, вырабатываемая валами трансмиссии. Мы можем быстро понять, как крутка генерирует мощность, просто выполнив простой размерный анализ. Мощность измеряется в единицах Вт [Вт] и 1 Вт = 1 Н·м·с ^-1 . В начале этого раздела мы отметили, что крутящий момент представляет собой крутящуюся пару, а это означает, что он имеет единицы измерения силы, умноженной на расстояние, или [Н·м]. Итак, по результатам проверки, чтобы генерировать мощность с крутящим моментом, нам нужно что-то, что происходит с заданной частотой f , поскольку частота имеет единицы Герц [Гц] или [с ^-1 ]. Таким образом, мощность на один оборот (2*pi) круглого стержня равна приложенному крутящему моменту, умноженному на частоту вращения, или:

В крайней правой части уравнения мы использовали соотношение, согласно которому угловая скорость, обозначаемая греческой буквой омега , равна частоте, умноженной на 2pi.

Статически неопределимые задачи

Одно уравнение, два неизвестных… мы уже шли по этому пути, прежде чем нам потребовалось что-то еще. Хотя тип нагрузки и деформации различен, статически неопределимых задач, связанных с кручением стержней, решаются точно так же, как и для конструкций с осевой нагрузкой. Начнем со свободной диаграммы тела скрученного стержня. Возьмем, к примеру, стержень на рисунке ниже, застрявший между двумя стенами.

Сразу же при осмотре вы должны заметить, что стержень приклеен к двум стенам, тогда как для статического равновесия была бы необходима только одна. Поддержек больше, чем необходимо: статически неопределимая . И статически неопределимое среднее, нарисуйте диаграмму свободного тела, просуммируйте силы в направлении x-, и вы получите одно уравнение с двумя неизвестными силами реакции. Итак, нам нужно учитывать наши деформации – для кручения, значит, обратимся к нашему уравнению, описывающему суперпозицию углов закручивания. Для этого уравнения мы должны отметить, что половина стержня сплошная, а другая половина полая, что влияет на то, как мы вычисляем J для каждой половинки.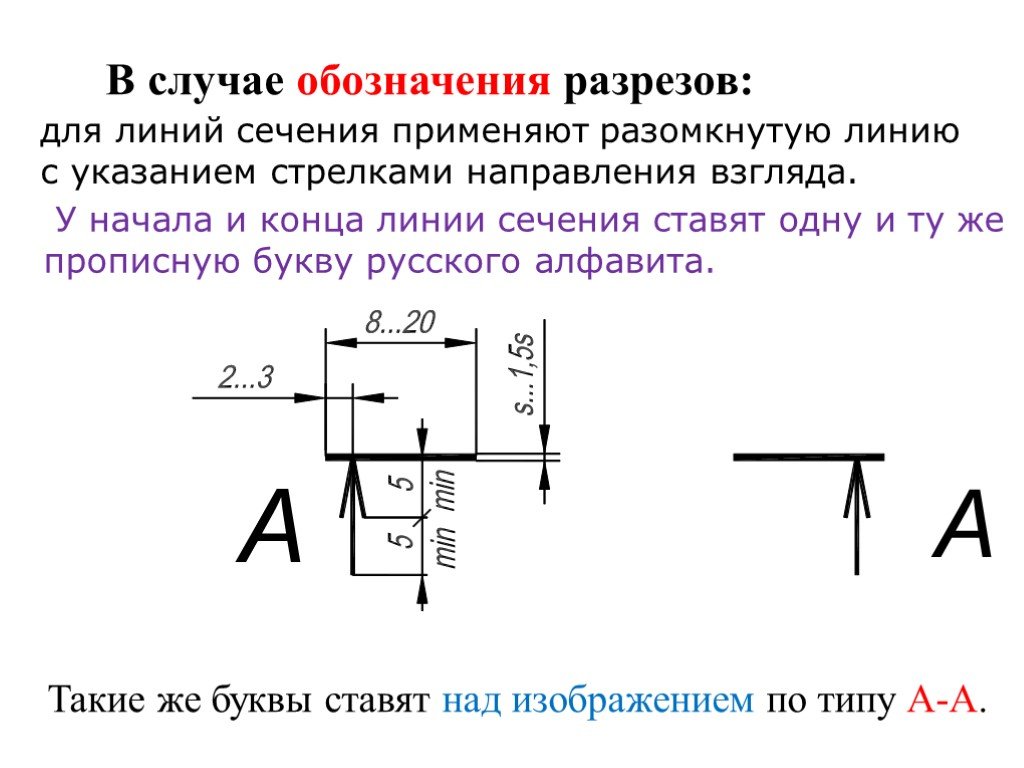 Самое главное, нам нужно спросить себя: «Что мы знаем о деформации?» Ну а так как стержень торцом прилеплен к стене, то закрутка на А и В должна быть равна нулю (как и смещение на последнем участке). Посмотрите, сможете ли вы решить оставшуюся часть этой задачи самостоятельно: каков крутящий момент в каждой половине стержня?

(Ответ: T _a = 51,7 фунта фут и T _b = 38,3 фунта фут).

Резюме

В этом уроке мы узнали о крутящем моменте и крутящем моменте . Этот другой тип нагрузки создает неравномерное распределение напряжения по поперечному сечению стержня — от нуля в центре до наибольшего значения на краю. Из этого анализа мы можем установить взаимосвязь между углом закручивания в любой точке стержня и деформацией сдвига внутри всего стержня. Используя закон Гука, мы можем связать этот штамм с напряжение внутри стержня.