Сечение плоскостью фигуры: Построение сечений
Содержание
Сечение геометрических тел плоскостями
Цель урока:
- Познакомить студентов с методами построения усечённых геометрических тел в прямоугольных проекциях.
- Изучить методы, позволяющие определять на чертеже действительную величину отрезка прямой и плоской фигуры.
- Формирование пространственных представлений студентов посредством чтения и построения чертежей.
- Совершенствование графической техники.
Учебные пособия и принадлежности:
Для преподавателя:
- усечённые геометрические модели.
- чертёжные инструменты и принадлежности.
Для студентов:
- рабочая тетрадь.
- чертёжные инструменты и принадлежности.
План урока:
1. Организационная часть Организационная часть— приветствие, проверка присутствующих на занятии, — объявление темы занятия, постановка целей и задач занятия, | 5 мин |
2. Изложение нового материала | 40 мин |
3. Закрепление новой темы | 35 мин |
4. | 5 мин |
5. Домашнее задание | 5 мин |
ПОНЯТИЕ О СЕЧЕНИЯХ ГЕОМЕТРИЧЕСКИХ ТЕЛ
Построение пересечения тел плоскостями часто встречается при изображении внешних очертаний деталей машин и приборов, при выявлении внутренних очертаний деталей и во вспомогательных построениях (нахождение точек встречи прямой с поверхностью, отыскание линий пересечения двух поверхностей и др.).
Детали машин и приборов очень часто имеют формы, представляющие собой различные геометрические поверхности. Пылесборник машины для очистки литых деталей (см. рис.1) представляет собой усеченный цилиндр. Форма крышки трубы пылесборника является фигурой сечения прямого кругового цилиндра и представляет собой эллипс. Пример сечения прямого кругового конуса приведен на рисунке 2. Колпак сепаратора представляет собой сварную конструкцию из тонкой листовой стали и состоит из двух конусов.
рис.1) представляет собой усеченный цилиндр. Форма крышки трубы пылесборника является фигурой сечения прямого кругового цилиндра и представляет собой эллипс. Пример сечения прямого кругового конуса приведен на рисунке 2. Колпак сепаратора представляет собой сварную конструкцию из тонкой листовой стали и состоит из двух конусов.
Рисунок 1
Рисунок 2
Кроме того, иногда необходимо выполнить развёртки поверхности полых деталей, усечённых плоскостью. Это применяется в раскрое листового материала, из которого изготовляются полые детали. Такие детали обычно представляют собой части всевозможных трубопроводов, вентиляционных устройств, кожухов для закрытия механизмов, ограждения станков и т.п. (см. рис.3).
Рисунок 3
При изучении темы «Пересечение поверхностей геометрических тел плоскостями» нужно обратить особое внимание на построение опорных точек при выполнении сечений.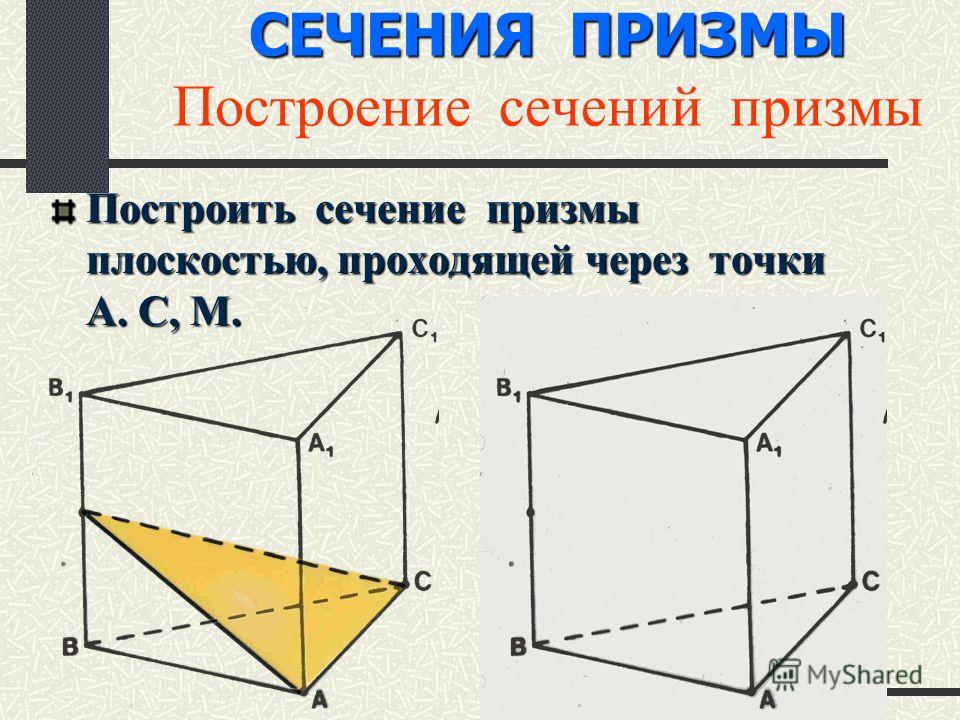
«Сечение – изображение фигуры, получающеёся при мысленном рассечении предмета одной или несколькими плоскостями. На сечении показывается только то, что получается непосредственно в секущей плоскости» (ГОСТ 2.305-68).
Построения прямоугольных и аксонометрических проекций усечённых тел, а также определение истинного вида сечений и развёрток поверхностей геометрических тел часто используются на практике.
Рассекая геометрическое тело плоскостью, получают сечение – ограниченную замкнутую линию, все точки которой принадлежат как секущей плоскости, так и поверхности тела.
Нужно обратить внимание на то, что при пересечении многогранника с плоскостью в сечении получается многоугольник с вершинами, расположенными на ребрах многогранника, а при пересечении тел вращения фигура сечения ограничена плавной кривой линией. Точки этой кривой находят с помощью вспомогательных линий, взятых на поверхности тела (например, образующих конуса и цилиндра).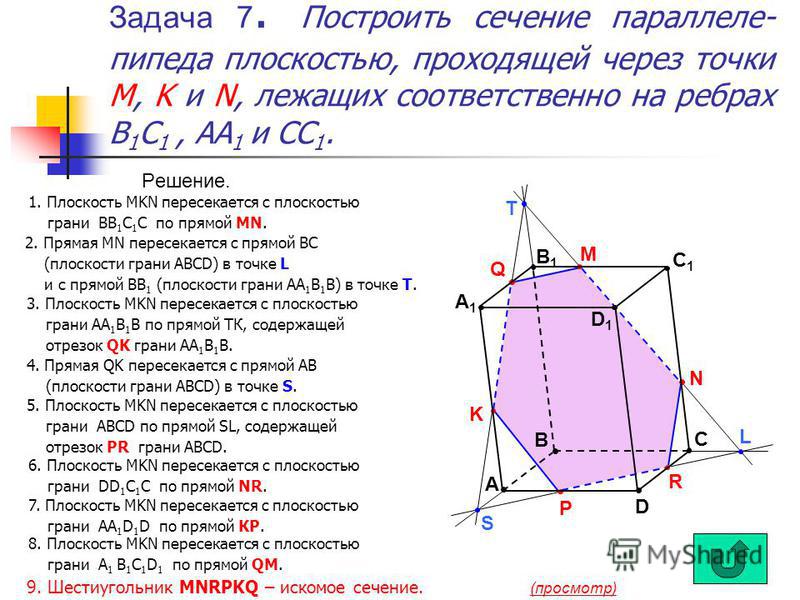 Точки пересечения образующих с секущей плоскостью будут принадлежать кривой линии сечения.
Точки пересечения образующих с секущей плоскостью будут принадлежать кривой линии сечения.
Для того чтобы определить действительную величину сечений, необходимо знать способы преобразования плоскостей проекций: способ вращения и способ перемены плоскостей проекций.
В качестве вспомогательных, к комплексным чертежам применяют аксонометрические проекции. Это делают в тех случаях, когда нужно дать наглядное изображение предмета.
Сечение призмы плоскостью
Из комплексного чертежа на рисунке 4, видно, что плоскость Рv пересекает не только боковую поверхность, но и верхнее основание призмы. Поэтому фигура сечения представляет собой плоский шестиугольник 1 2 3 4 5 6. Для построения проекций фигуры сечения находят проекции точек пересечения плоскости Рvс ребрами призмы и соединяют их прямыми линиями.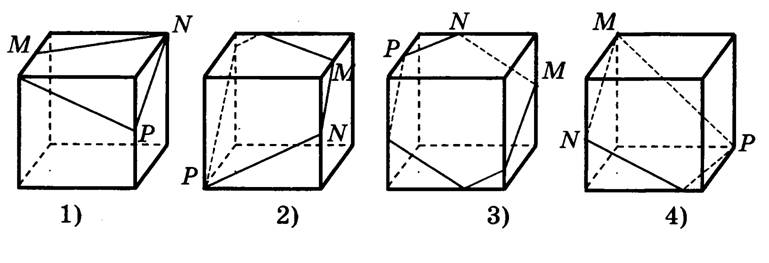 Фронтальные проекции этих точек получаются при пересечении фронтальных проекций ребер призмы со следом Рv, секущей плоскости Р (точки 1` — 6`).
Фронтальные проекции этих точек получаются при пересечении фронтальных проекций ребер призмы со следом Рv, секущей плоскости Р (точки 1` — 6`).
Горизонтальные проекции точек пересечения 1-6 совпадают с горизонтальными проекциями ребер.
Имея фронтальные и горизонтальные проекции этих точек, с помощью линий связи находят профильные проекции 1″ — 6» Полученные точки соединяют прямыми линиями и получают профильную проекцию фигуры сечения.
Действительный вид фигуры сечения можно определить любым из способов: вращения, совмещения или перемены плоскостей проекций.
В данном примере (см. рис. 4) применён способ перемены плоскостей проекций. Горизонтальная плоскость проекций заменена новой плоскостью, причём ось х1, для упрощения построений, параллельна фронтальному следу плоскости Р.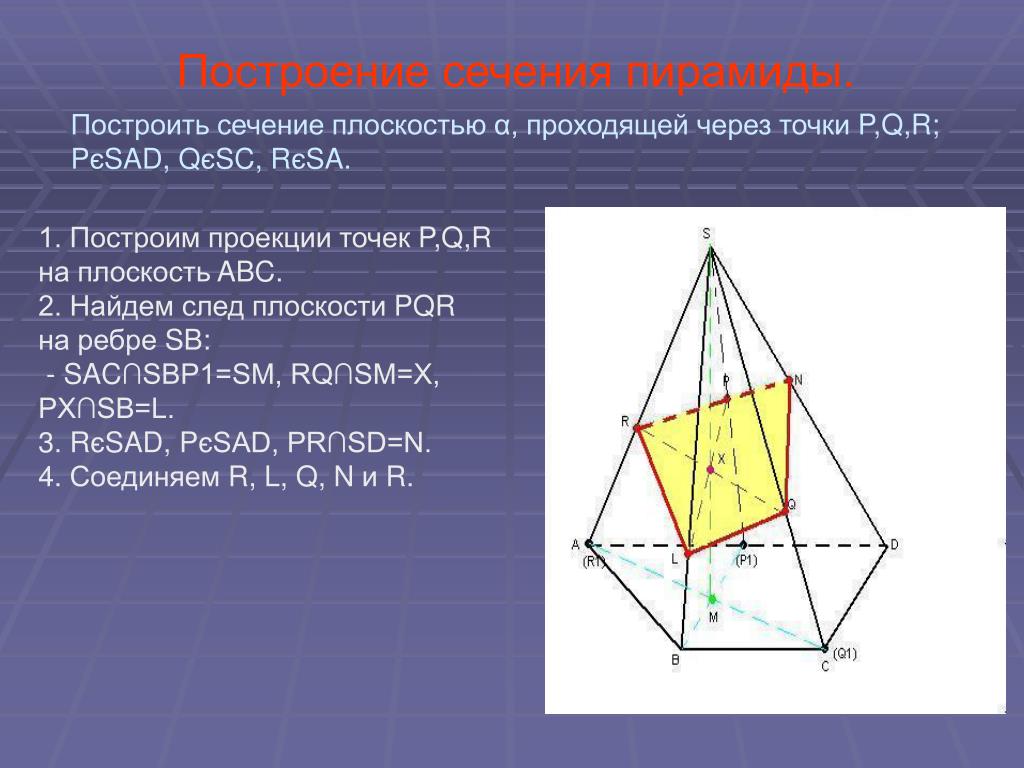
Для нахождения новой горизонтальной проекции какой-либо точки фигуры сечения (например, точки 1) необходимо выполнить следующие построения. Из точки 1′ , на фронтальном следе плоскости Р, восстанавливают перпендикуляр к новой оси х1, и откладывают на нем расстояние от прежней оси х до прежней горизонтальной проекции точки 1, т.е. отрезок n1. В результате получают точку 11. Таким же способом построения находят и остальные горизонтальные проекции точек 21-61. Соединив прямыми линиями новые горизонтальные проекции 11-61, получают натуральную величину фигуры сечения (см. рис.4).
Рисунок 4 Вы можете посмотреть здесь.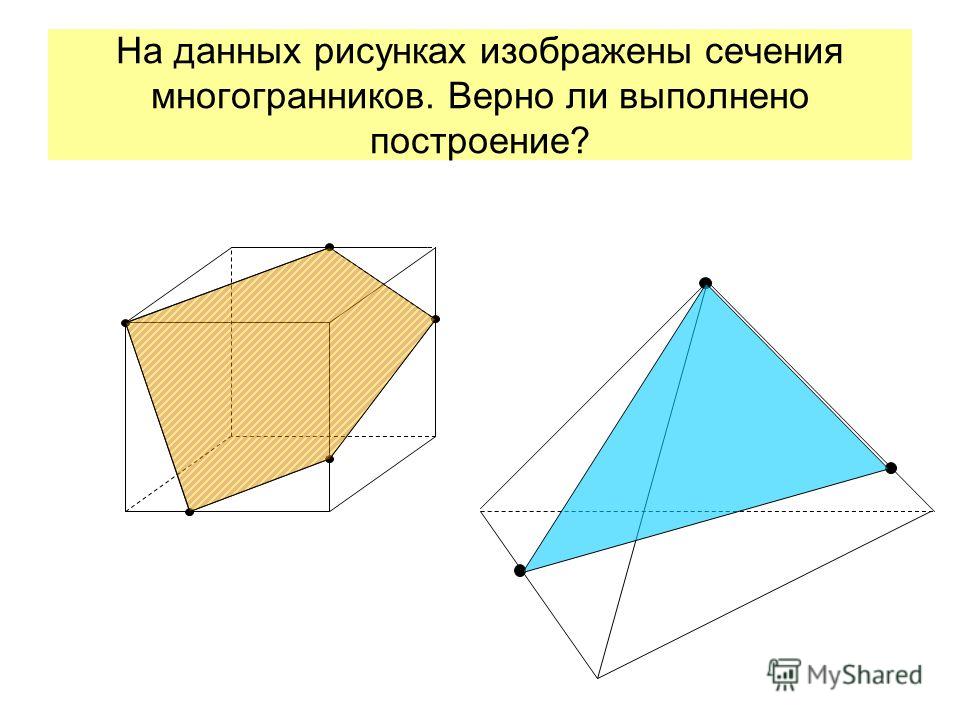
Сечение цилиндра плоскостью
Построение плоского сечения прямого кругового цилиндра аналогично построению плоского сечения призмы, так как прямой круговой цилиндр можно рассматривать как прямую призму с бесчисленным количеством ребер — образующих цилиндра.
На рисунке 5 даны три проекции прямого кругового цилиндра, пересеченного фронтально-проецирующей плоскостью Р.
Из комплексного чертежа видно, что фронтально-проецирующая плоскость Р пересекает не только боковую поверхность, но и верхнее основание цилиндра. Как известно, плоскость, расположенная под угломк оси цилиндра, пересекает его по эллипсу. Следовательно, фигура сечения в данном случае представляет собой часть эллипса.
Натуральная величина фигуры сечения, получена способом перемены плоскостей проекций. Горизонтальная плоскость проекций заменена новой. Новая ось проекций выполнена совпадающей с плоскостью Р, (построение аналогично рис.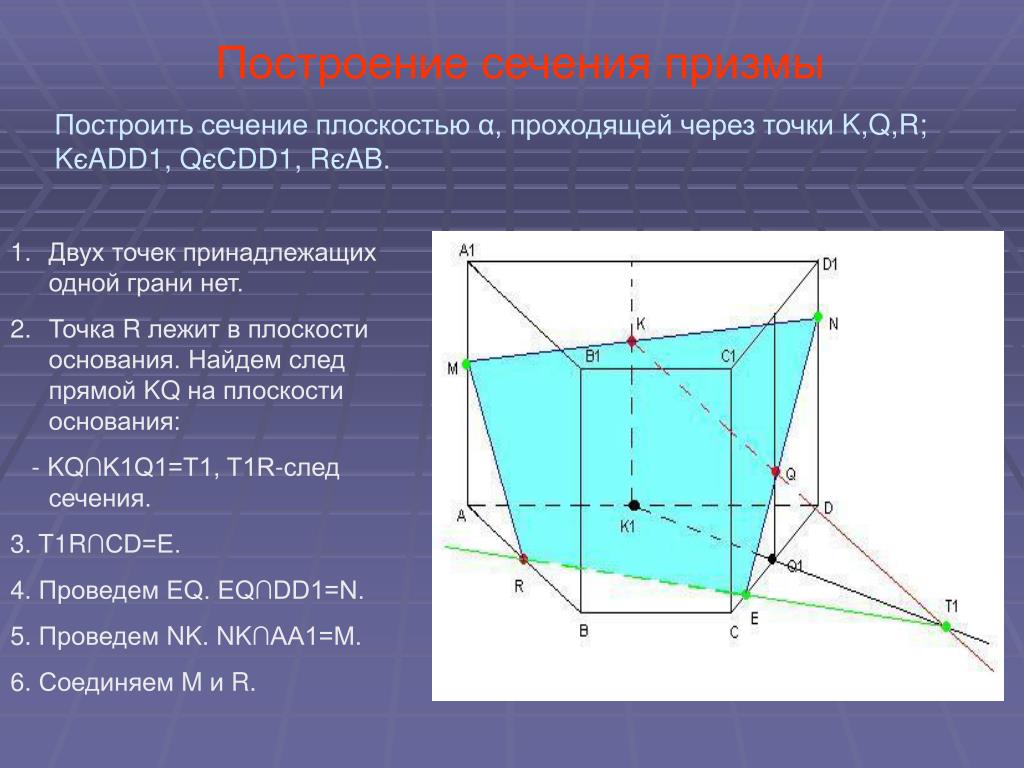 4).
4).
Рисунок 5 Вы можете посмотреть здесь.
Сечение пятигранной пирамиды плоскостью
Правильная пятигранная пирамида, пересеченная фронтально-проецирующей плоскостью Р, показана на рисунке 7.
Как и в предыдущих примерах, фронтальная проекция сечения совпадает с фронтальным следом Pv плоскости. Горизонтальную и профильную проекции фигуры сечения строят по точкам, которые являются точками пересечения плоскости Р с ребрами пирамиды. Натуральная величина фигуры сечения может быть найдена, например, способом совмещения.
Указание: Нахождение натуральной величины отрезка (бокового ребра пирамиды) (см. рис. 6).
Пусть требуется определить действительный вид боковых ребер пирамиды.
Рисунок 6
Как видно из рисунка, рёбра пирамиды горизонтально-проецирующие, поэтому действительный вид рёбер треугольника можно получить на плоскости V (на виде спереди) вращением любого из рёбер вокруг вертикальной оси до тех пор, пока проекция ребра не станет параллельна плоскости V.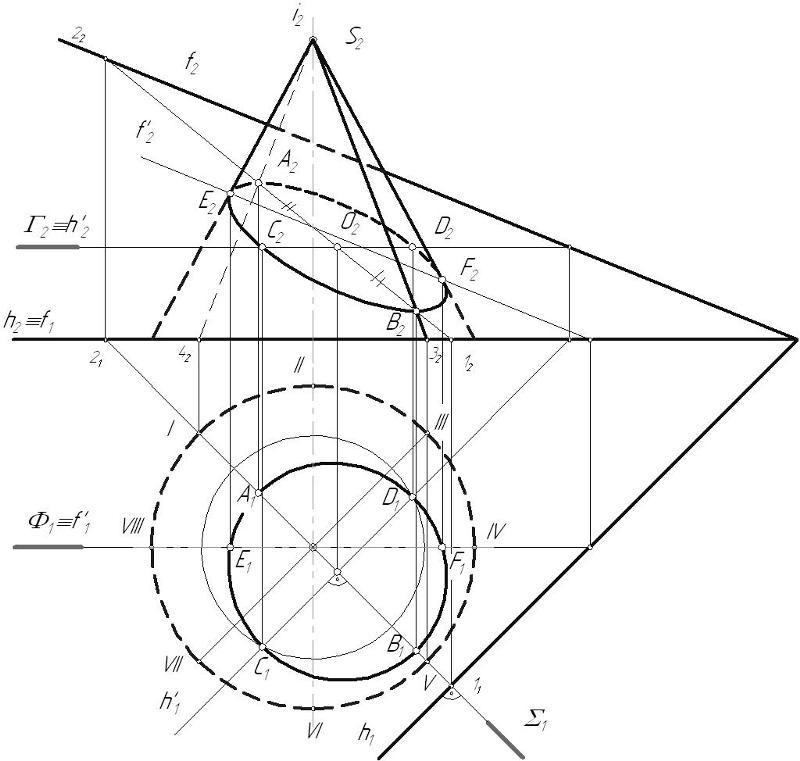
На комплексном чертеже (см. рис.6) ось вращения 2‘S, перпендикулярная плоскости H, проведена через вершину треугольника S. Вращается вершина рёбра треугольника точка 2. После поворота, новая горизонтальная проекция ребра треугольника S 21 должна быть параллельна оси х. Фронтальную проекцию — точки 21‘ — вершины 2 после поворота находят, проводя вертикальную линию связи вверх до оси х из точки 21. Соединив точки 21‘ и S‘, получим на плоскости V (на виде спереди) действительную величину ребра S 2 треугольной пирамиды.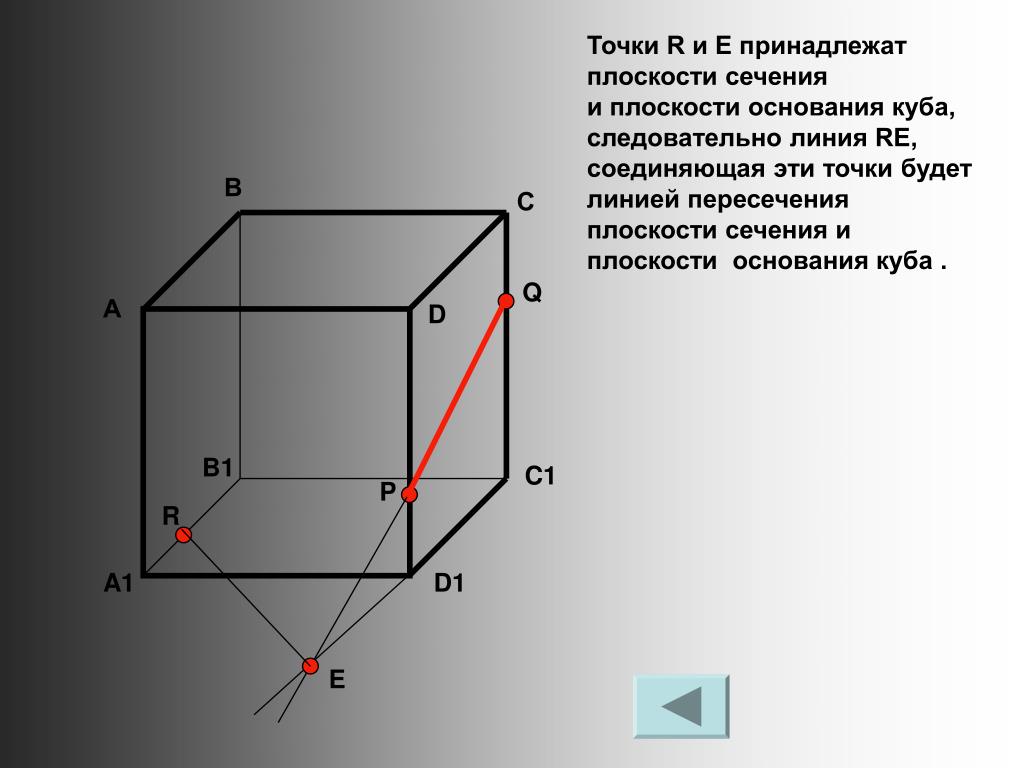
Рисунок 7 Вы можете посмотреть здесь.
Сечение прямого кругового конуса плоскостью
При различном расположении секущей плоскости Р по отношению к оси прямого кругового конуса получают различные фигуры сечения, ограниченные большей частью кривыми линиями.
Сечение прямого кругового конуса фронтально-проецирующей плоскостью Р рассматривается на рисунке 8. Основание конуса расположено на горизонтальной плоскости Н. Фигура сечения в данном случае будет ограничена эллипсом.
Для построения горизонтальной проекции контура фигуры сечения – горизонтальную проекцию основания конуса (окружность) делят, например, на 12 равных частей. Через точки деления на горизонтальной и фронтальной проекциях проводят вспомогательные образующие. Сначала находят фронтальные проекции точек сечения 1` — 12`, лежащих на фронтальном следе плоскости Рv. Затем с помощью линий связи находят их горизонтальные проекции. Например, горизонтальная проекция точки 2, расположенной на образующей S2, проецируется на горизонтальную проекцию этой же образующей S2 в точку 2.
Затем с помощью линий связи находят их горизонтальные проекции. Например, горизонтальная проекция точки 2, расположенной на образующей S2, проецируется на горизонтальную проекцию этой же образующей S2 в точку 2.
Найденные горизонтальные проекции точек контура сечения соединяют по лекалу. Действительный вид фигуры сечения в данном примере найден способом перемены плоскости проекций. Плоскость Н заменяется новой плоскостью проекции Н1. Чтобы получить новую горизонтальную проекцию какой-либо точки проекции эллипса, например точки 21, из точки 2′ восстанавливают перпендикуляр и откладывают на нем отрезок равный отрезку 2′ — 2, т.е. расстояние n (см. рис.8).
Рисунок 8 Вы можете посмотреть здесь.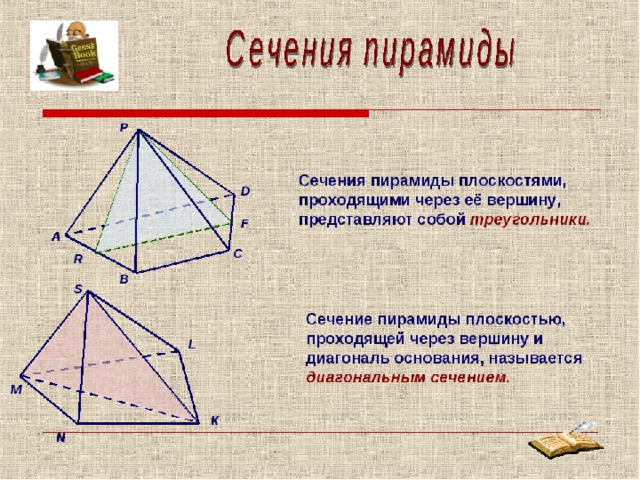
Самостоятельная работа по теме: «Сечение геометрических тел плоскостями» (Приложение).
Литература
Основная:
Учебники
- В.Г.Григорьев, В.И.Горячев, Т.П.Кузнецова Инженерная графика/ Серия «Учебники, учебные пособия». – Ростов н/Д: Феникс, 2004.
- С.К. Боголюбов Черчение – М.: Машиностроение, 2002. ил. И.С.Вышнепольский, В.И. Вышнепольский Черчение для техникумов: Учеб. для учеб. заведений нач. и сред. проф. образования – М.: ООО «ИздательствоАстрель»: ООО «Издательство АСТ», 2002., ил.
- И.А.Ройтман, Я.В.Владимиров Черчение: Учеб. Пособие для уч-ся 9 кл. общеобразовательных учреждений. – М.: Гуманит. изд. центр ВЛАДОС, 2001., ил.
- Р.С. Миронова, Б.Г.Миронов Инженерная графика – М.: Высш. школа, 2000., ил.
- А.Потёмкин Инженерная графика. Просто и доступно – Москва: издательство «Лори», 2000.
Дополнительная:
Сборники заданий
- Боголюбов С.
 К. Задания по курсу инженерной графики. – М.: Машиностроение, 2004.
К. Задания по курсу инженерной графики. – М.: Машиностроение, 2004. - Миронова Р.С., Миронов Б.Г. Сборник задач по инженерной графике. Учебное пособие. – М.: Высшая школа, 2000.
- Пакеты прикладных программ компьютерной графики профессиональной деятельности.
Сечение геометрических тел плоскостями.
Понятие о сечении и линии пересечения
В результате пересечения геометрического тела плоскостью получается плоская фигура, которую называют сечением (или фигурой сечения).
В общем случае сечение представляет собой плоскую фигуру, ограниченную замкнутой линией, все точки которой принадлежат как секущей плоскости, так и поверхности тела.
При пересечении плоскостью многогранных геометрических тел (призмы, пирамиды, параллелепипеда и т. п.) в общем случае получается замкнутая ломаная линия, состоящая из отдельных отрезков прямых линий, точки излома линии пересечения являются точками пересечения ребер многогранной фигуры плоскостью.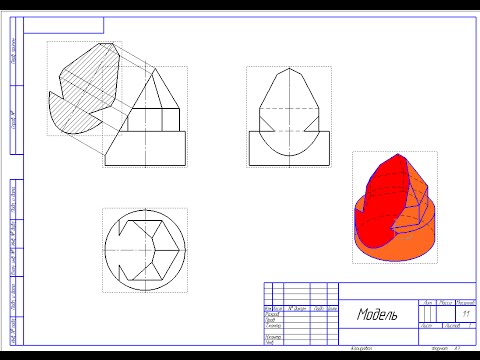
Если фигура представляет собой тело вращения (цилиндр, конус, шар и т. п.) или ее поверхность ограничена плавными кривыми поверхностями, линией сечения будет кривая, для построения которой необходимо определить характерные точки, расположенные на очерковых образующих, точки, удаленные на максимальное и минимальное расстояние от плоскости проекции, а также произвольные точки линии сечения. При этом чем больше точек пересечения плоскостью такой фигуры будет определено, тем правильнее будет построена линия пересечения.
***
Пересечение тел проецирующими плоскостями.
Построение действительной величины фигуры сечения.
При пересечении геометрических тел плоскостью проецирующего положения (т. е. перпендикулярной одной из плоскостей проекции) одна из проекций сечения изображается прямой линией, совпадающей с линейной (вырожденной) проекцией плоскости, т. е. сечение фигуры на этом виде представляет собой прямую, которая может быть параллельна какой-либо оси проекций (х, у или z), либо располагаться под наклоном к ней.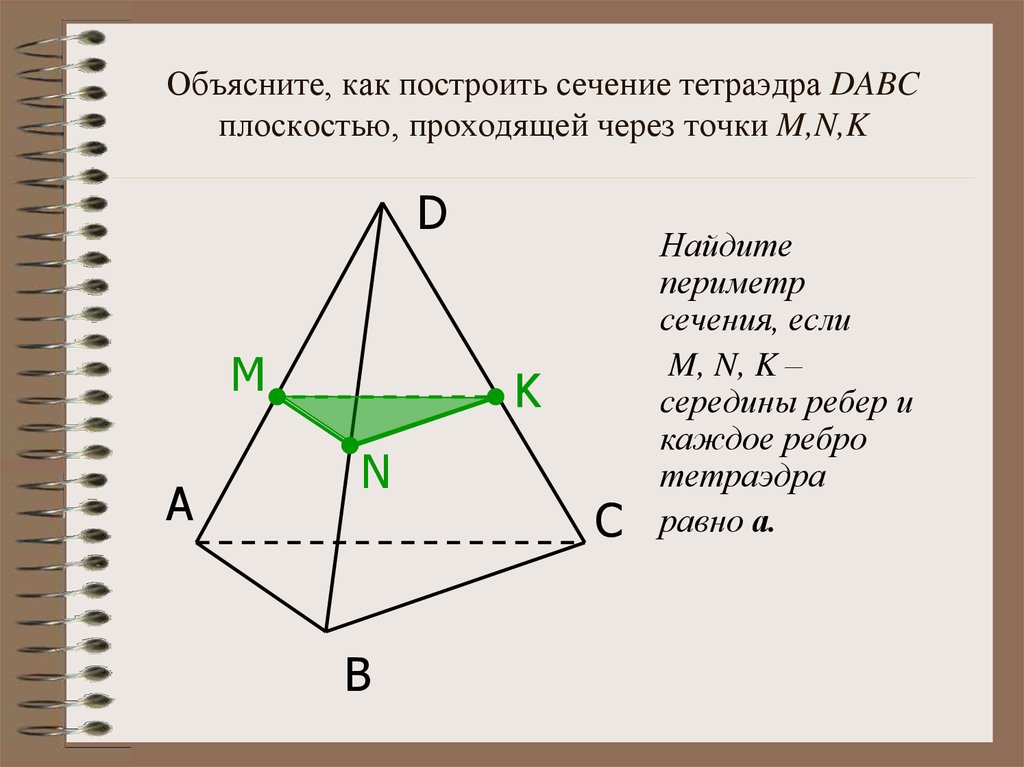 Остальные проекции сечения определяют по характерным точкам пересечения плоскости с ребрами фигуры методом прямоугольного проецирования.
Остальные проекции сечения определяют по характерным точкам пересечения плоскости с ребрами фигуры методом прямоугольного проецирования.
***
Пересечение многогранников плоскостью
При пересечении многогранника плоскостью частного положения грани будут пересекаться по прямым линиям, и линией пересечения будет замкнутая или незамкнутая ломаная линия. Для построения этой линии достаточно найти точки пересечения ребер с заданной плоскостью (опорные точки) и соединить их с учетом видимости.
Пример пересечения призмы плоскостью
Задача
Построить линию пересечения призмы ABCD плоскостью а (рис. 1). Определить действительную величину фигуры сечения.
Решение.
Плоскость а является фронтально-проецирующей.
Фронтальная проекция сечения вырождается в прямую 1-2-3-4, совпадающую со следом а, секущей плоскости.
Горизонтальная проекция совпадает с горизонтальной проекцией основания ABCD.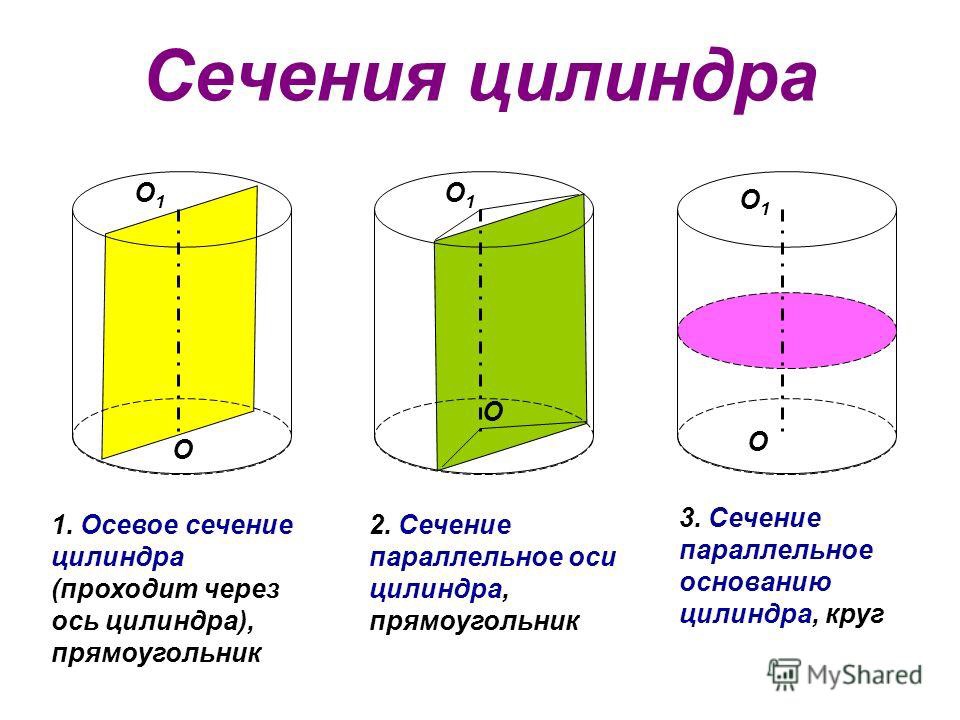 Профильная проекция строится по точкам.
Профильная проекция строится по точкам.
Действительную величину сечения 12-22-З2-42 определяют способом плоскопараллельного перемещения.
***
Пример пересечения пирамиды плоскостью
Задача
Построить линию пересечения пирамиды плоскостью а (рис. 2). Определить действительную величину сечения.
Решение
Т. к. плоскость а фронтально-проецирующая, то не требуется дополнительных построений. Фронтальный след плоскости совпадает с фронтальной проекцией сечения.
На пересечении ребер с фронтальным следом плоскости находим точки 7…4, линии сечения.
По точкам 7, 2, 3 и 4 на ребрах пирамиды строим горизонтальную и профильную линию сечения.
Действительную величину сечения 7-2-3-4 определяем способом замены плоскостей проекций.
Порядок построения показан на рис. 2.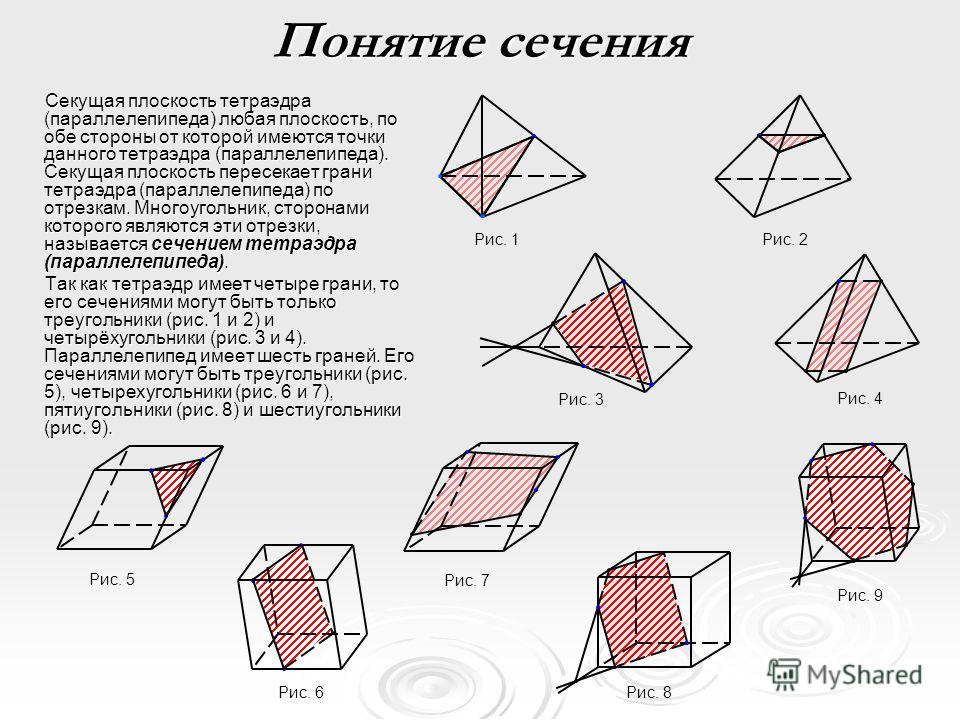 Фигура 1-4 и есть действительная величина сечения.
Фигура 1-4 и есть действительная величина сечения.
Выполняем третью проекцию по координатам точек вершин. Соединив полученные точки прямыми линиями, получаем третью проекцию пирамиды с линией пересечения плоскостью.
***
Пересечение поверхностей вращения плоскостью
Пересечение цилиндра плоскостью
В сечении цилиндра плоскостью частного положения могут быть получены следующие линии (рис. 3):
- окружность, если секущая плоскость а перпендикулярна к оси вращения;
- эллипс, если секущая плоскость у не перпендикулярна и не параллельна к оси вращения;
- две образующие (прямые линии), если секущая плоскость параллельна образующим или оси поверхности.
Задача
Построить линию пересечения прямого кругового цилиндра фронтально проецирующей плоскостью а (рис. 4). Определить действительную величину сечения.
Решение
Секущая плоскость а относительно оси цилиндра расположена под острым углом. В этом случае линия пересечения на поверхности цилиндра расположенная в плоскости сечения, представляет собой эллипс с центром О на оси цилиндра; большая ось эллипса равна отрезку 12-72, а малая — диаметру цилиндра.
В этом случае линия пересечения на поверхности цилиндра расположенная в плоскости сечения, представляет собой эллипс с центром О на оси цилиндра; большая ось эллипса равна отрезку 12-72, а малая — диаметру цилиндра.
Т. к. плоскость а пересекает верхнее основание цилиндра, сечение имеет вид плоской фигуры, ограниченной дугой эллипса и отрезком прямой АВ.
Проекция фигуры сечения на виде сверху совпадает с проекцией цилиндра. На плоскости П1 сечение строится по координатам характерных точек, которые затем соединяются плавной кривой.
Действительная величина сечения построена с помощью способа плоскопараллельного пересечения. Проекция сечения 7,-7, располагается горизонтально и из точек проводят перпендикуляры. На пересечении с линиями, проведенными из точек 11-121 получаем точки 1-12 и АВ. Соединив их последовательно, получаем действительную величину сечения.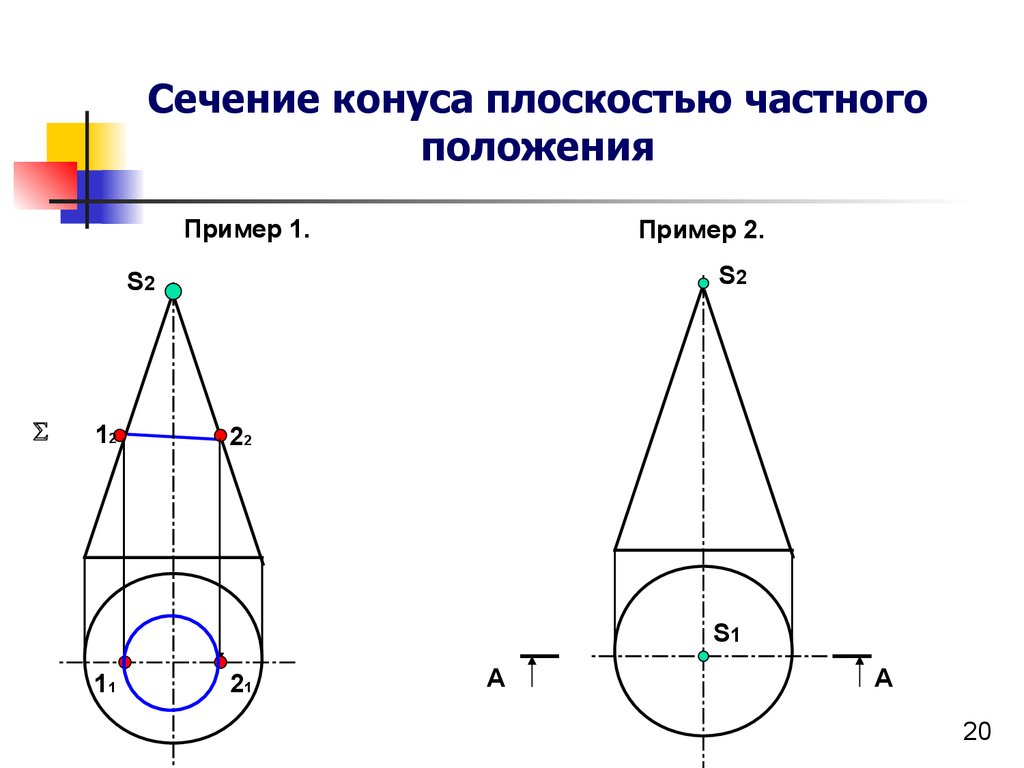
Пересечение прямого кругового конуса плоскостью
Поверхность прямого кругового конуса является носителем кривых второго порядка — окружности, эллипса, параболы и гиперболы. Все эти кривые являются плоскими и могут быть получены в результате пересечения конической поверхности плоскостью. Чтобы получить ту или иную кривую второго порядка, необходимы условия, которые могут быть установлены из свойств этих кривых.
Чтобы получить в сечении получился эллипс, плоскость должна пересекать все образующие конической поверхности. В частном случае, когда диаметры равны (секущая плоскость перпендикуляра оси конической поверхности), в сечении получается окружность (рис. 5, а).
Чтобы в сечении получить параболу, секущая плоскость должна быть параллельна одной из образующих конуса. В пределе, когда секущая плоскость переходит в касательную, две симметричные дуги параболы преобразуются в две совпадающие прямые (рис. 5, б).
Гипербола в сечении получается, если секущая плоскость параллельна двум прямолинейным образующим конуса.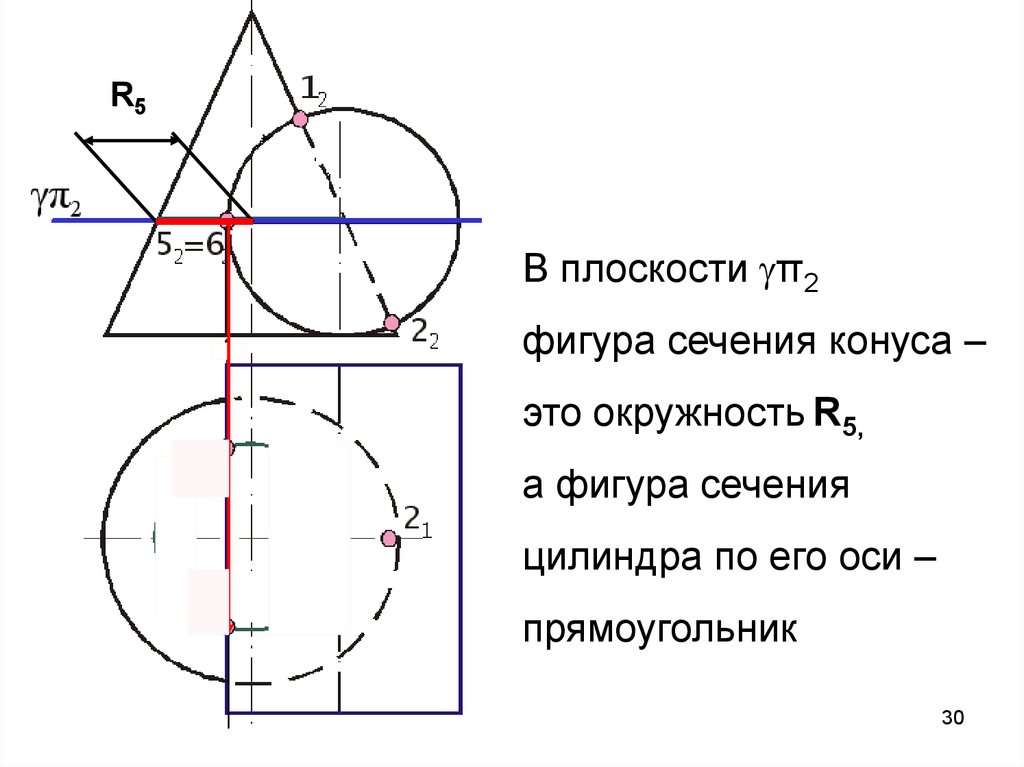
В частном случае, когда секущая плоскость проходит через вершину конической поверхности, гипербола распадается на две пересекающиеся прямые (рис. 5, в).
Пример построения действительной фигуры сечения и линии пересечения конуса плоскостью показан на рис. 6.
***
Построение линий пересечения поверхностей способом вспомогательных сфер
Главная страница
- Страничка абитуриента
Дистанционное образование
- Группа ТО-81
- Группа М-81
- Группа ТО-71
Специальности
- Ветеринария
- Механизация сельского хозяйства
- Коммерция
- Техническое обслуживание и ремонт автотранспорта
Учебные дисциплины
- Инженерная графика
- МДК.
 01.01. «Устройство автомобилей»
01.01. «Устройство автомобилей» - Карта раздела
- Общее устройство автомобиля
- Автомобильный двигатель
- Трансмиссия автомобиля
- Рулевое управление
- Тормозная система
- Подвеска
- Колеса
- Кузов
- Электрооборудование автомобиля
- Основы теории автомобиля
- Основы технической диагностики
- Основы гидравлики и теплотехники
- Метрология и стандартизация
- Сельскохозяйственные машины
- Основы агрономии
- Перевозка опасных грузов
- Материаловедение
- Менеджмент
- Техническая механика
- Советы дипломнику
Олимпиады и тесты
- «Инженерная графика»
- «Техническая механика»
- «Двигатель и его системы»
- «Шасси автомобиля»
- «Электрооборудование автомобиля»
Как рассчитать площадь поперечного сечения
Обновлено 7 февраля 2020 г.
Кевин Бек
Вы можете столкнуться с ситуациями, когда у вас есть трехмерная твердотельная фигура и вам нужно вычислить площадь воображаемой плоскости, вставленной через фигуру и имеющей границы, определяемые границами твердого тела.
Например, если под вашим домом проходит цилиндрическая труба длиной 20 метров (м) и диаметром 0,15 м, вам может понадобиться узнать площадь поперечного сечения трубы.
Поперечные сечения могут быть перпендикулярны оси твердого тела, если таковые существуют. В случае сферы любая секущая плоскость, проходящая через сферу, независимо от ориентации, приведет к диску определенного размера.
Площадь поперечного сечения зависит от формы твердого тела, определяющей границы поперечного сечения, и угла между осью симметрии твердого тела (если она есть) и плоскостью, создающей поперечное сечение.
Площадь поперечного сечения прямоугольного тела
Объем любого прямоугольного тела, включая куб, равен площади его основания (длина, умноженная на ширину), умноженной на его высоту: V = l × w × h.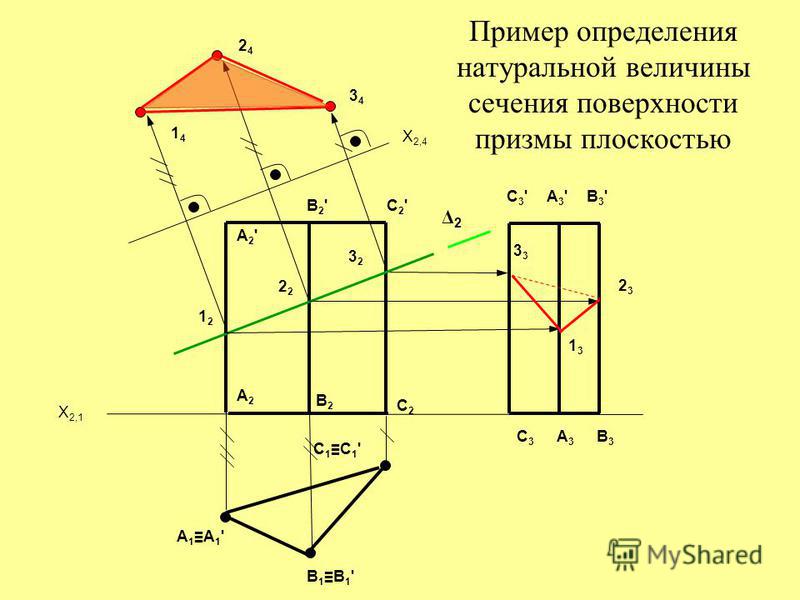
Следовательно, если поперечное сечение параллельно верхней или нижней части твердого тела, площадь поперечного сечения равна l × w. Если секущая плоскость параллельна одному из двух наборов сторон, площадь поперечного сечения вместо этого определяется как l × h или w × h.
Если поперечное сечение не перпендикулярно какой-либо оси симметрии, созданная форма может быть треугольником (если провести через угол тела) или даже шестиугольником.
Пример: Вычислить площадь поперечного сечения плоскости, перпендикулярной основанию куба объемом 27 м 3 .
Так как для куба l = w = h, длина любого ребра куба должна быть 3 м (поскольку 3
× 3
× 3 = 27). Таким образом, поперечное сечение описанного типа представляет собой квадрат со стороной 3 м, что дает площадь 9 м 2 .
Площадь поперечного сечения цилиндра
Цилиндр представляет собой твердое тело, образованное путем вытягивания окружности через пространство перпендикулярно ее диаметру.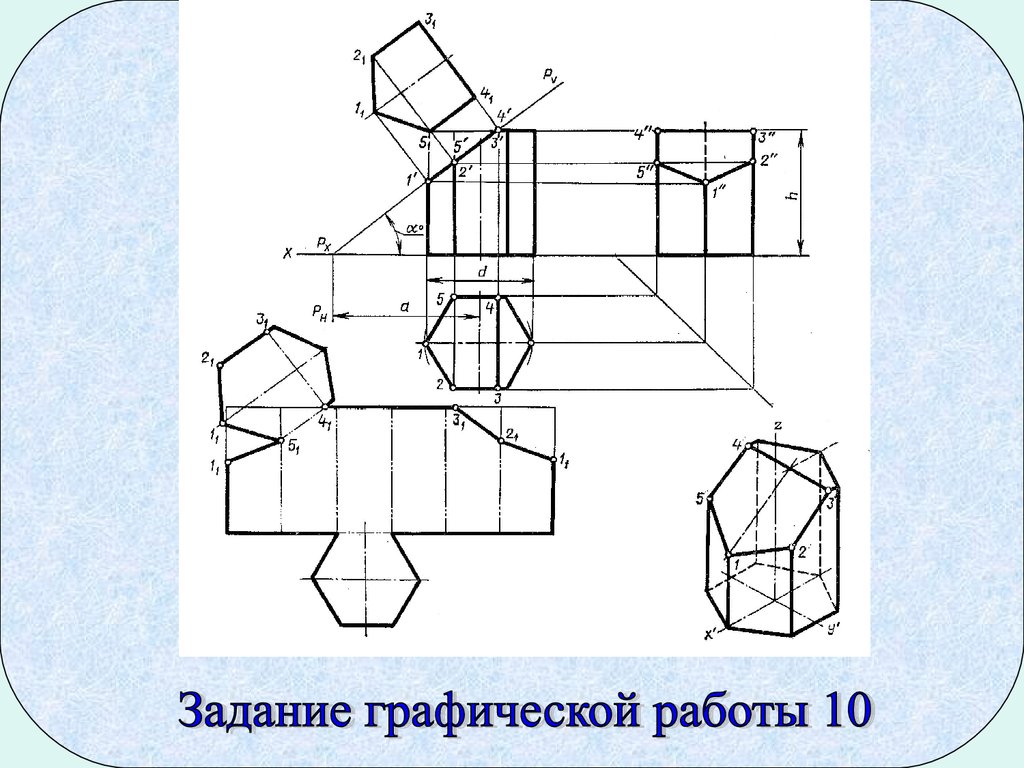 Площадь круга находится по формуле πr 2 , где r — радиус. Поэтому имеет смысл, что объем цилиндра будет площадью одной из окружностей, образующих его основание.
Площадь круга находится по формуле πr 2 , где r — радиус. Поэтому имеет смысл, что объем цилиндра будет площадью одной из окружностей, образующих его основание.
Если поперечное сечение параллельно оси симметрии, то площадь поперечного сечения представляет собой просто круг площадью πr 2 . Если секущая плоскость вставляется под другим углом, создается эллипс. Для площади используется соответствующая формула: πab (где а — самое большое расстояние от центра эллипса до края, а b — самое короткое).
Пример: Какова площадь поперечного сечения трубы под вашим домом, описанной во введении?
Площадь поперечного сечения сферы
Любая теоретическая плоскость, проведенная через сферу, даст круг (подумайте об этом несколько минут). Если вы знаете диаметр или длину окружности, образуемой поперечным сечением, вы можете использовать соотношения C = 2πr и A = πr 2 для получения решения.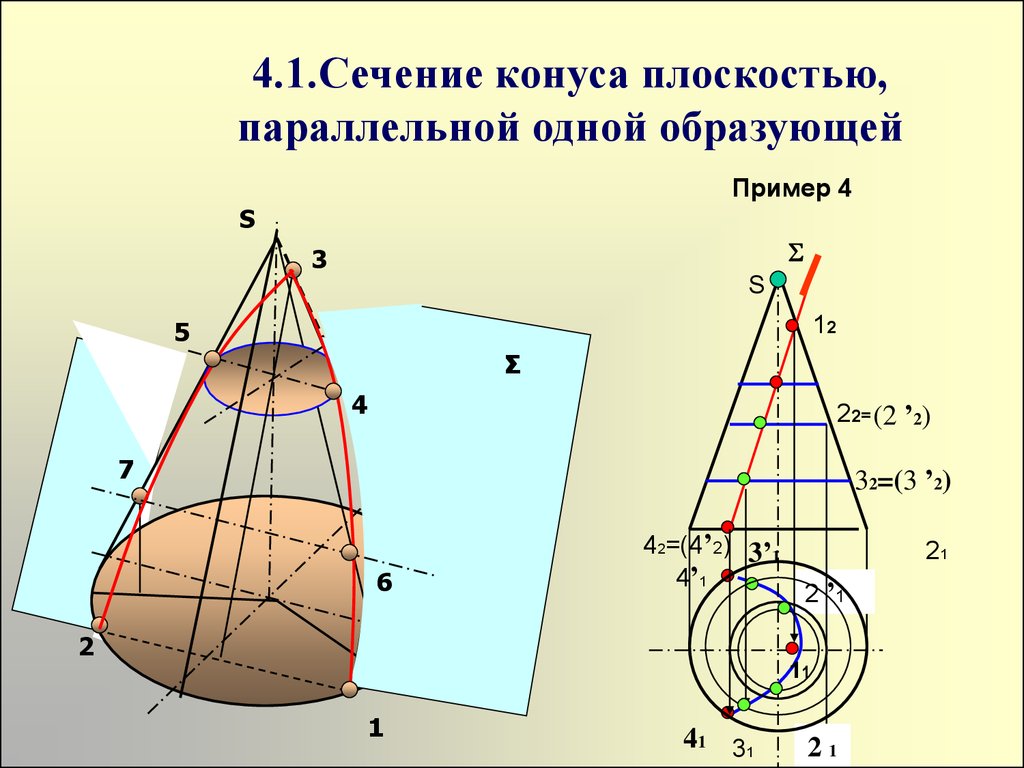
Пример 900:12: Самолет грубо вставлен в Землю очень близко к Северному полюсу, удаляя часть планеты в 10 м вокруг. Какова площадь поперечного сечения этого холодного куска Земли?
- Поскольку C = 2πr = 10 м, r = 10/2π = 1,59 м; A = πr 2 = π(1,59) 2 = 7,96 м 2 .
Поперечное сечение
Поперечное сечение представляет собой пересечение данного объекта плоскостью вдоль его оси. В геометрии сечением называется непустое пересечение твердого тела плоскостью. Разрезание объекта на срезы создает множество параллельных поперечных сечений, которые дополнительно создают несколько форм, таких как круг, прямоугольник и т. д.
Не обязательно, чтобы объект был трехмерным, эту концепцию можно применять и к двумерным формам.
Например, если самолет прорезает горы на двухмерной карте, результатом будут точки на поверхности гор с одинаковой высотой.
Кроме того, вы можете понять концепцию поперечного сечения, изучая ее на примерах в реальном времени, например, дерево после того, как оно было срублено, имеет форму кольца, это помогает нам понять меньшую часть, увеличив ее.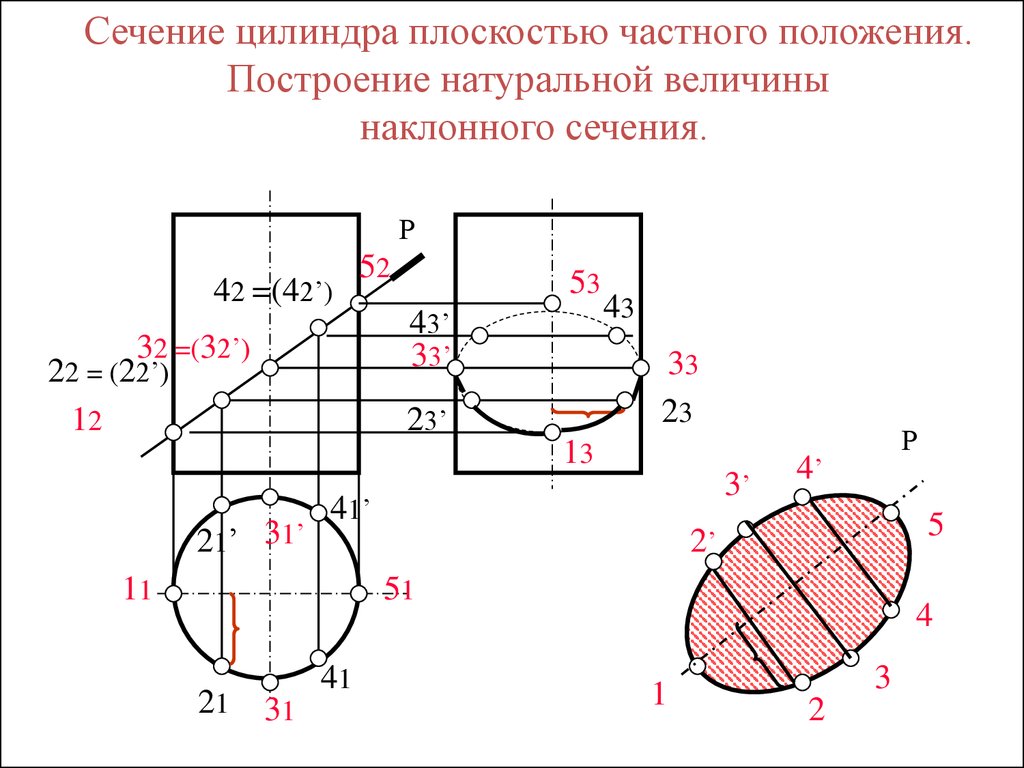
В геометрии мы изучаем различные типы фигур, одномерную форму, двумерную форму и так далее. Концепция поперечных сечений играет важную роль в лучшем понимании этих форм, поэтому мы будем продвигаться вперед в концептуальном понимании поперечных сечений по их определению, типам и относительным примерам.
Что такое поперечное сечение?
Поперечное сечение определяется как форма, полученная в результате пересечения твердого объекта плоскостью. Поперечное сечение трехмерной формы представляет собой двумерную геометрическую форму.
Типы поперечных сечений
Существует два основных типа поперечных сечений, а именно:
* Горизонтальное поперечное сечение
* Вертикальное поперечное сечение
Горизонтальное поперечное сечение
Горизонтальное поперечное сечение, также известное как параллельное поперечное сечение -сечение — это когда плоскость разрезает твердое тело в горизонтальном направлении так, что создается параллельное поперечное сечение с основанием.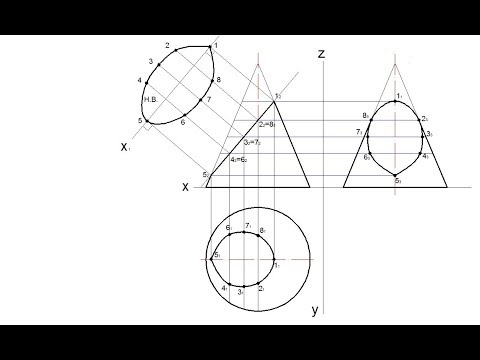 Например, горизонтальное сечение цилиндра представляет собой круг.
Например, горизонтальное сечение цилиндра представляет собой круг.
Вертикальное поперечное сечение
В перпендикулярном поперечном сечении плоскость разрезает твердое тело в вертикальном направлении, перпендикулярном его основанию. Например, вертикальное сечение цилиндра представляет собой прямоугольник.
Примеры поперечных сечений
Некоторые общеизвестные примеры поперечных сечений:
* Любое поперечное сечение сферы может быть кругом
* Вертикальное поперечное сечение конуса может быть треугольником, и поэтому горизонтальное поперечное сечение может быть кругом
* Вертикальное поперечное сечение цилиндра может быть прямоугольником, и, следовательно, горизонтальное поперечное сечение может быть кругом
Сечение в геометрии
Прежде чем мы поймем различные поперечные сечения трехмерной формы, мы поняли бы важные термины и функции, относящиеся к ней.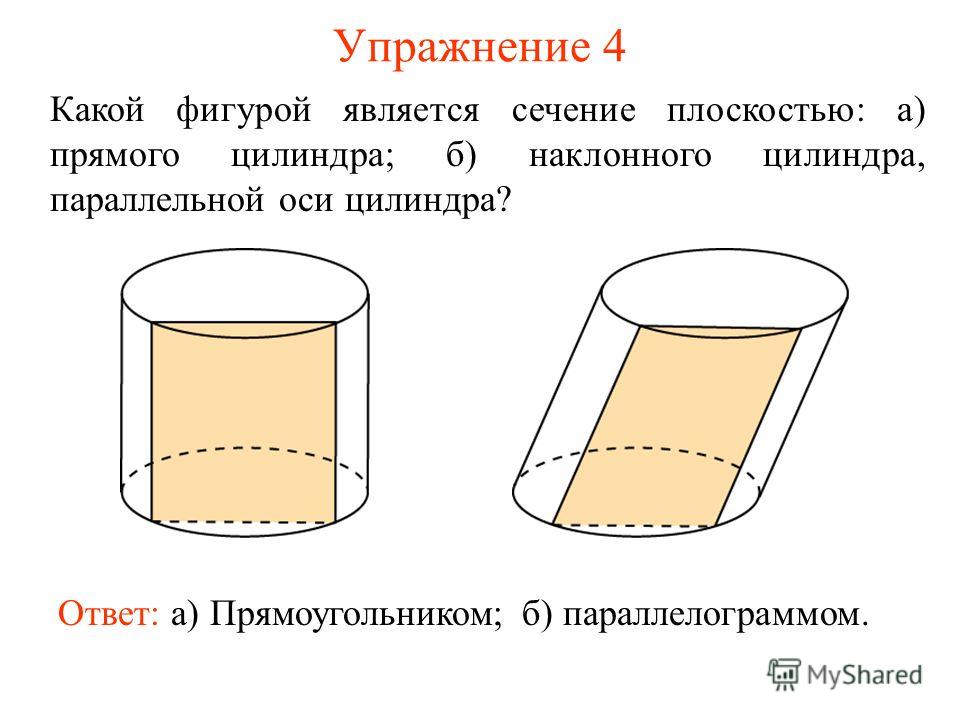
Площадь поперечного сечения и объем
Что такое площадь поперечного сечения?
Когда твердый объект пересекается плоскостью, область проецируется на плоскость. Эта плоскость далее перпендикулярна оси своей симметрии; таким образом, эта проекция называется площадью поперечного сечения.
Формула площади поперечного сечения = l x w
Объем поперечного сечения
Объем твердого тела определяется интегралом площади поперечного сечения.
Поперечное сечение конуса
Конус представляет собой пирамидальную структуру с круглым основанием и треугольной вершиной. Поперечное сечение конуса называется коническим сечением, это достигается за счет зависимости между плоскостью и наклонной поверхностью. Это может быть круг, парабола, эллипс.
Поперечные сечения цилиндра
Цилиндр может иметь различную форму в зависимости от способа его огранки, он может быть кругом, прямоугольником или овалом.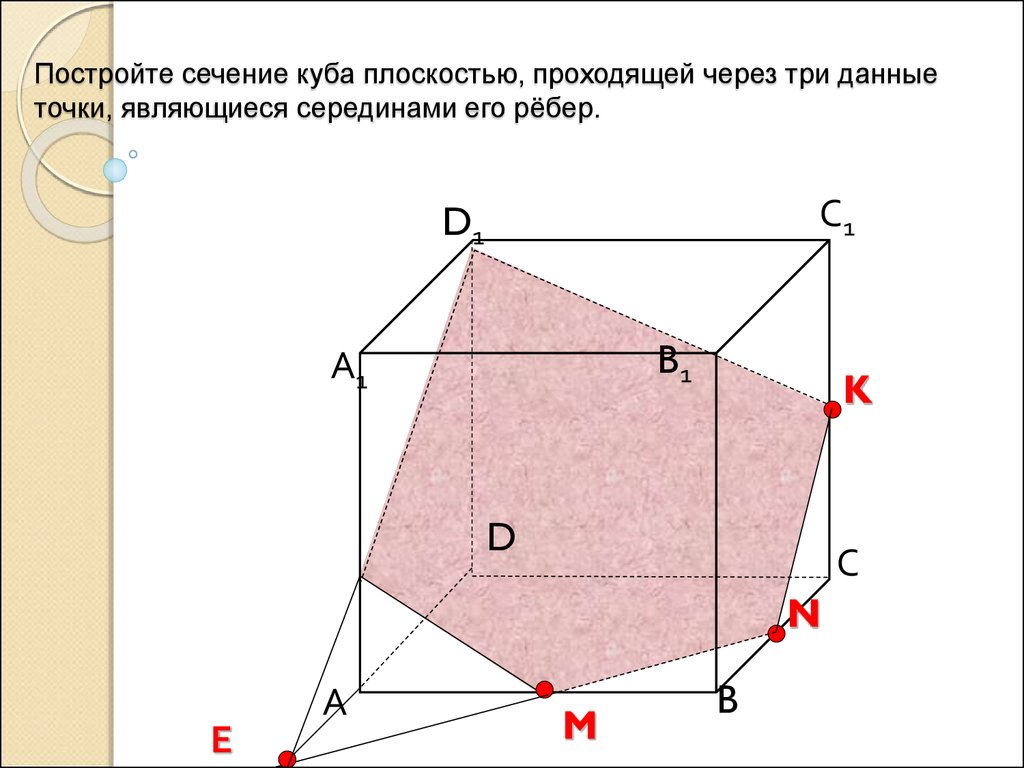
Если цилиндр имеет горизонтальное поперечное сечение, то форма будет кругом. Если плоскость основания цилиндра перпендикулярна его основанию, то форма будет прямоугольником.
Овальная форма получается, когда плоскость пересекает цилиндр параллельно основанию с изменением его угла.
Поперечное сечение сферы
Сфера представляет собой круглую твердую фигуру, поверхность которой, каждая точка которой равноудалена от ее центра.
Сфера имеет наименьшую площадь для своего объема. Пересечение плоскости со сферой дает окружность, точно так же все сечения сферы являются окружностями.
Пример поперечного сечения Решенная задача
Задача 1: Определить площадь поперечного сечения заданного цилиндра высотой 25 см и радиусом 4 см.
Решение:
Дано:
Радиус = 4 см
Высота = 25 см
Мы знаем, что когда плоскость разрезает цилиндр параллельно дну, то полученное поперечное сечение может быть кругом.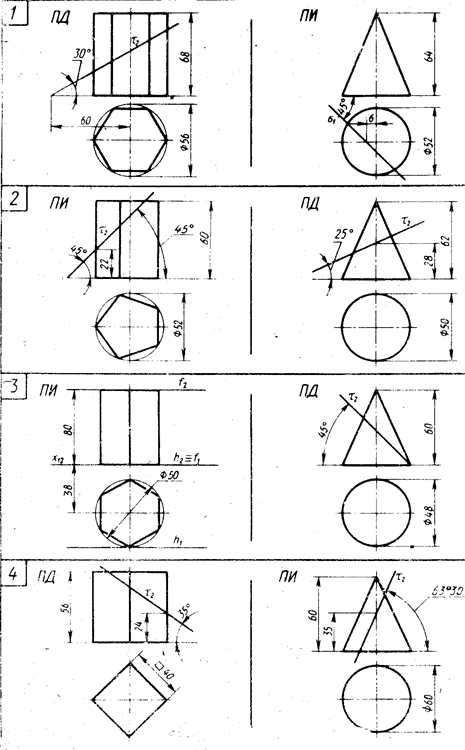
 Заключение
Заключение К. Задания по курсу инженерной графики. – М.: Машиностроение, 2004.
К. Задания по курсу инженерной графики. – М.: Машиностроение, 2004. 01.01. «Устройство автомобилей»
01.01. «Устройство автомобилей»