Сечение в геометрии: Геометрия Решение задач на построение сечений
Содержание
Геометрия Решение задач на построение сечений
Материалы к уроку
Конспект урока
Решение задач на построение сечений
|
Подумайте, какой школьный предмет позволяют научиться правильно выполнять и оформлять чертежи, познакомится с различными графическими способами передачи сведений об объектах предметного мира.
Правильно! Это черчение.
Для изготовления деталей на заводе используются точные чертежи этих деталей в разрезе.
Разрезы используются для показа внутренней формы изделия.
Разрезом называется изображение, полученное при мысленном рассечении детали одной или несколькими секущими плоскостями. В разрезах показывается то, что получается в секущей плоскости.
|
На экране изображение
На экране изображение
На экране рисунок
| ||||
|
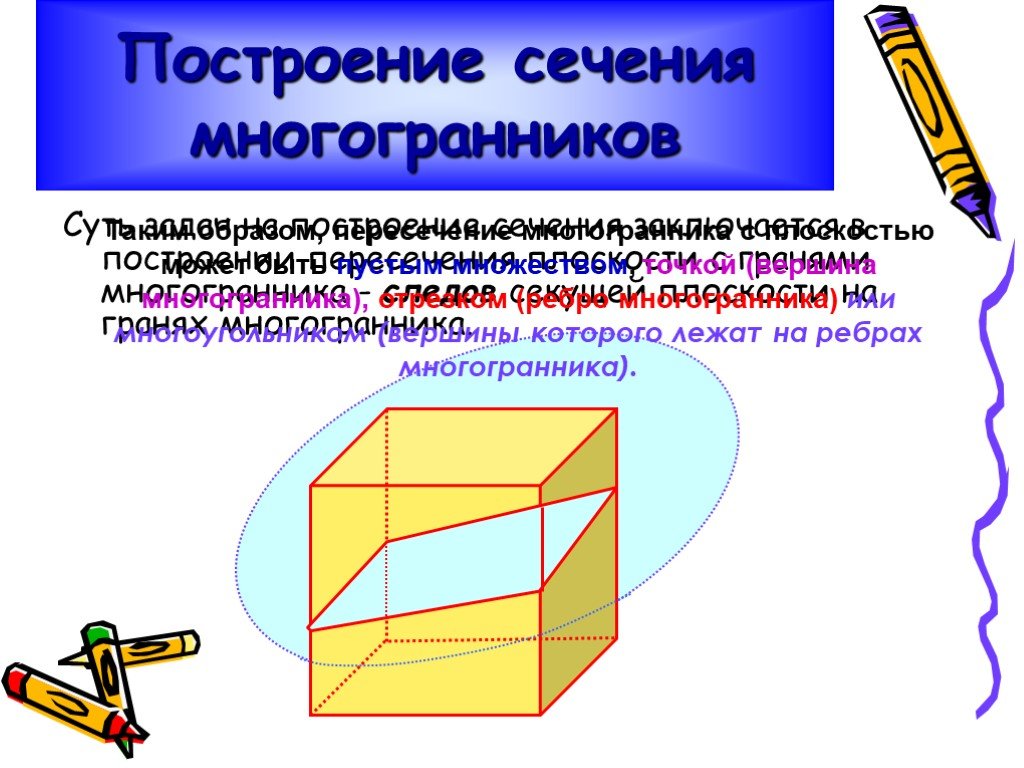
При решении геометрических задач связанных с тетраэдром и параллелепипедом тоже иногда необходимо построить разрез фигуры. Только полученное изображение в геометрии называется сечением.
Давайте разберёмся, что называется сечением тетраэдра и параллелепипеда.
|
| ||||
|
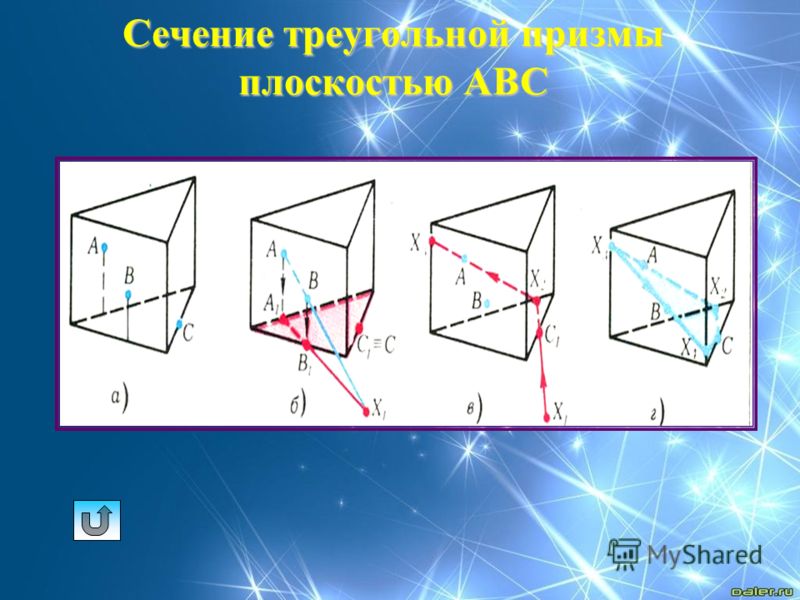
Секущая плоскость α пересекает грани тетраэдра по отрезкам АЕ, ЕС, АС.
Тетраэдр имеет четыре грани, значит его сечениями могут быть только треугольники и четырехугольник.
При пересечении параллелепипеда секущая плоскость также оставляет следы на его боковых гранях в виде отрезков.
Так как у параллелепипеда шесть граней, то в сечении может получиться фигура треугольник,
на рисунке вы это видите. Четырехугольник
Пятиугольник и шестиугольник .
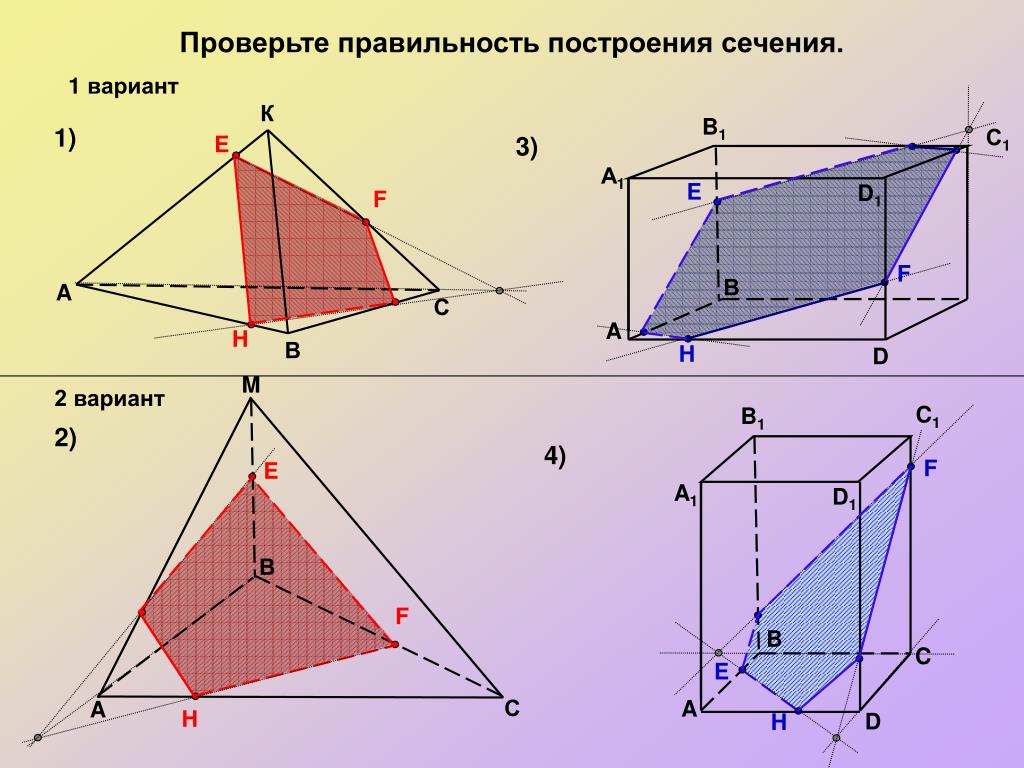
При построении сечений очень легко нарушить геометрические факты, теоремы. Например, данное сечение параллелепипеда плоскостью содержит ошибку.
Если плоскость пересекает две параллельные плоскости, то линии их пересечения параллельны.
Исправим ошибки.
Или на данном чертеже прямая LM пересекает ребро ВC в точке N. Но это невозможно. Прямая LM принадлежит плоскости АА1D1D, а прямая ВС не лежит в данной плоскости, значит они не могут пересекаться, они скрещивающиеся прямые. Так прямая LM не может пересекать DC, ВВ1 , а вот c прямой AD они пересекаются.
Исправим ошибку на чертеже.
|
На экране текст и изображение:
Сечение тетраэдра
На экране изображение и текст:
Виды сечений тетраэдра
На экране изображение и текст:
Сечение параллелепипеда
На экране изображение и текст:
Виды сечений параллелепипеда
На экране изображение:
На экране обновляется изображение
На экране обновляется чертёж
| ||||
|
Рассмотрим примеры построения различных сечений.
Дан тетраэдр АВСD . На его рёбрах отмечены точки K,L,M. Построить сечение тетраэдра плоскостью, проходящей через точки K,L,M.
Изобразим тетраэдр и данные точки.
При построении сечений нужно помнить один факт, что если две плоскости имеют общие точки, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Так у нас секущая плоскость проходит чрез точки M,L, а они лежат в плоскости CDB, значит ML-линия пересечения плоскостей.
Аналогично прямая KL является линией пересечения секущей плоскости и грани ADB
Для того чтобы построить линию пересечения с гранью АВС нужны две точки.
Для построения второй точки. Продлим до пересечения прямые KL и АВ. Отметим их общую точку S. Точка S принадлежит секущей плоскости, так как ей принадлежит прямая KL и принадлежит грани АВС, так как ей принадлежит прямая АВ. Значит секущая плоскость пересекает плоскость АВС по прямой MS.
Построим эту прямую. Отметим точку P- точку пересечения прямой с ребром АС. Отрезок PM- след от сечения грани плоскостью α.
Мы получили в результате две точки K и Р В грани АDC.
Четырехугольник KLMP-искомое сечение.
|
На экране текст.
Дан тетраэдр АВСD . На его рёбрах отмечены точки K,L,M. Построить сечение тетраэдра плоскостью, проходящей через точки K,L,M.
| ||||
|
Рассмотрим задачу на построение сечения параллелепипеда.
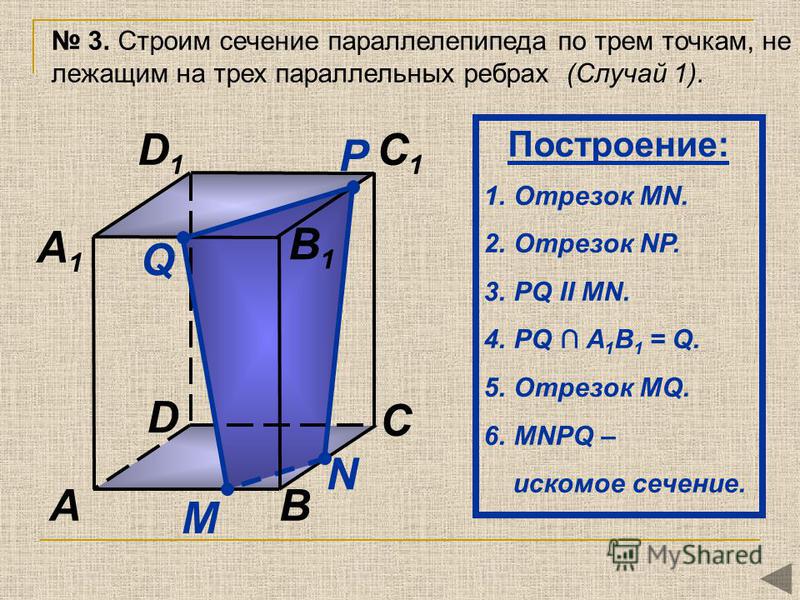
На рёбрах параллелепипеда даны точки K,L,M. Построить сечение параллелепипеда плоскостью KLM.
Построим данный параллелепипед и отметим указанные точки.
Так как точки L и M принадлежат грани АА1D1D и секущей плоскости, значит прямая LM их линия пересечения, а отрезок LM след от сечения грани АА1D1D секущей плоскостью.
Аналогично в грани DD1C1C построим прямую MK и выделим отрезок MK.
В грани А1B1C1D1 есть только одна точка L, для построения второй точки продлим до пересечения прямые D1C1 и MK. Отметим их общую точку H.
Точка H принадлежит секущей плоскости, так принадлежит прямой MK.
Так как точки T и К принадлежат секущей плоскости и грани ВВ1С1С, то отрезок ТК будет следом от сечения в этой грани.
Выделим получившийся четырехугольник KMLT. Это искомое сечение.
Рассмотренные задачи относятся к классу задач на построение и имеют свои этапы решения: анализ, построение, доказательство.
|
На экране текст:
На рёбрах CC1,A1D1, DD1 параллелепипеда АВСDA1B1C1D1 отмечены точки K,L,M соответственно. Построить сечение параллелепипеда плоскостью KLM.
|
Комментарий: задачи разобраны очень подробно, оформлены, четко структурированы. были небольшие опечатки по ходу решения.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Задачи на построение сечений.
 Аксиомы и теоремы стереометрии (урок геометрии в 10 классе)
Аксиомы и теоремы стереометрии (урок геометрии в 10 классе)
2015-2016
УЧЕБНЫЙ ГОД
Аксиомы и теоремы стереометрии
В
А
α
А2. Если две точки
прямой лежат в
плоскости, то все точки
прямой лежат в этой
плоскости.
Аксиомы и теоремы стереометрии
β
А
α
a
А3. Если две плоскости
имеют общую точку, то
они имеют общую
прямую, на которой
лежат все общие точки
этих плоскостей.
Аксиомы и теоремы стереометрии
Если две параллельные
плоскости пересечены
третьей, то линии их
пересечения
параллельны.
β
α
γ
Сечения тетраэдра и параллелепипеда
Задача 1. Построить сечение плоскостью, проходящей
через данные точки D, Е, K.
Построение:
S
1. DE
2. ЕК
3. ЕК ∩ АС = F
4. FD
5. FD ∩ BС = M
6. KM
DЕKМ – искомое сечение
E
K
А
С
M
D
В
F
Задача 2. Построить сечение плоскостью, проходящей
через точки Р, К, М, М∈ВС.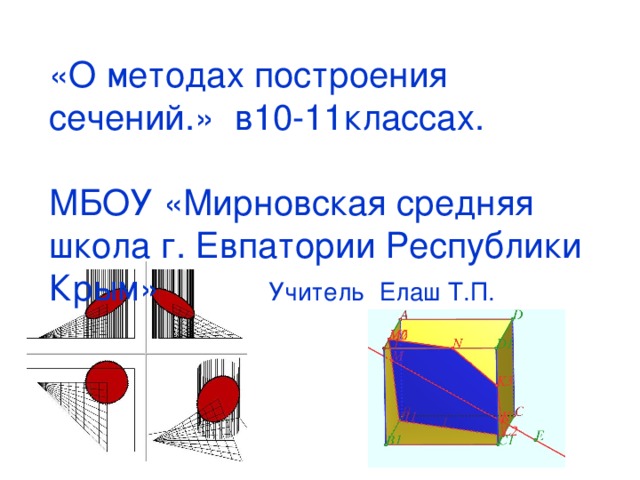
Построение:
В1
К
А1
C1
Р
D1
N
М
В
А
С
Р1
E
К1
D
1. КP
2. EM ║ КP (К1Р1)
3. EK
4. МN ║ EK
5. РN
KРNМE – искомое сечение
Задача 3. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
1. НМ
1. МТ
1. НT
D1
Н
Т
М
А
В
С
D
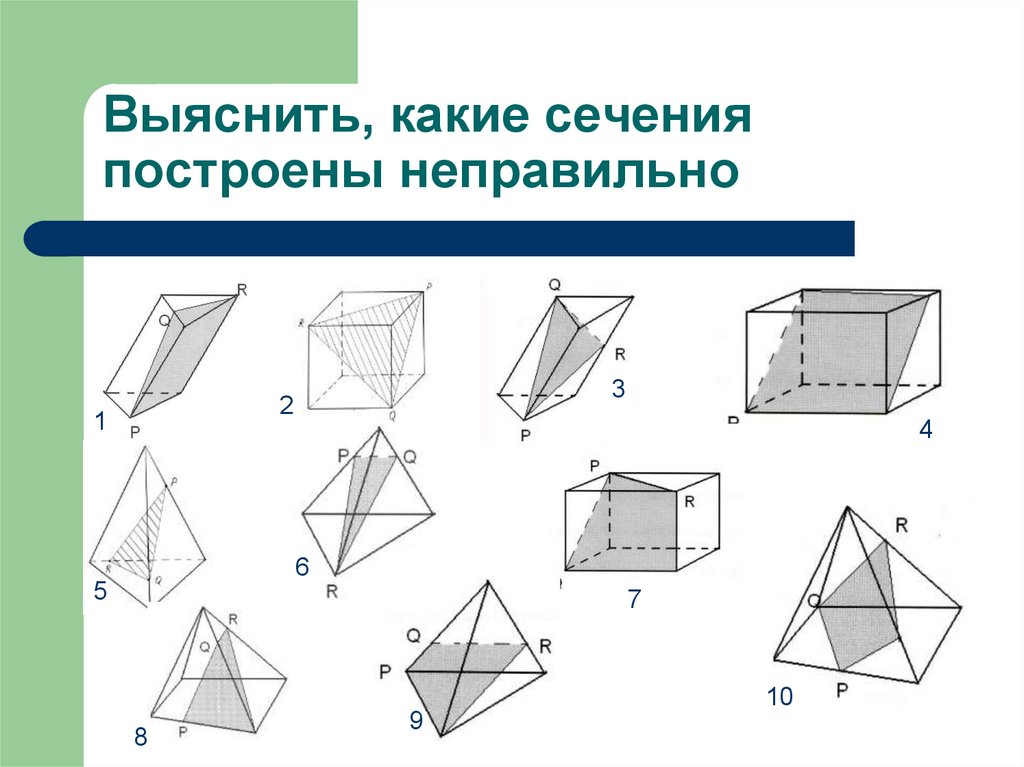
Выберите верный вариант:
Задача 3. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
1. НМ
Комментарии:
Данные точки
принадлежат разным
граням!
С
D
Назад
Задача 3. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
1. МT
Комментарии:
Данные точки
принадлежат разным
граням!
С
D
Назад
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.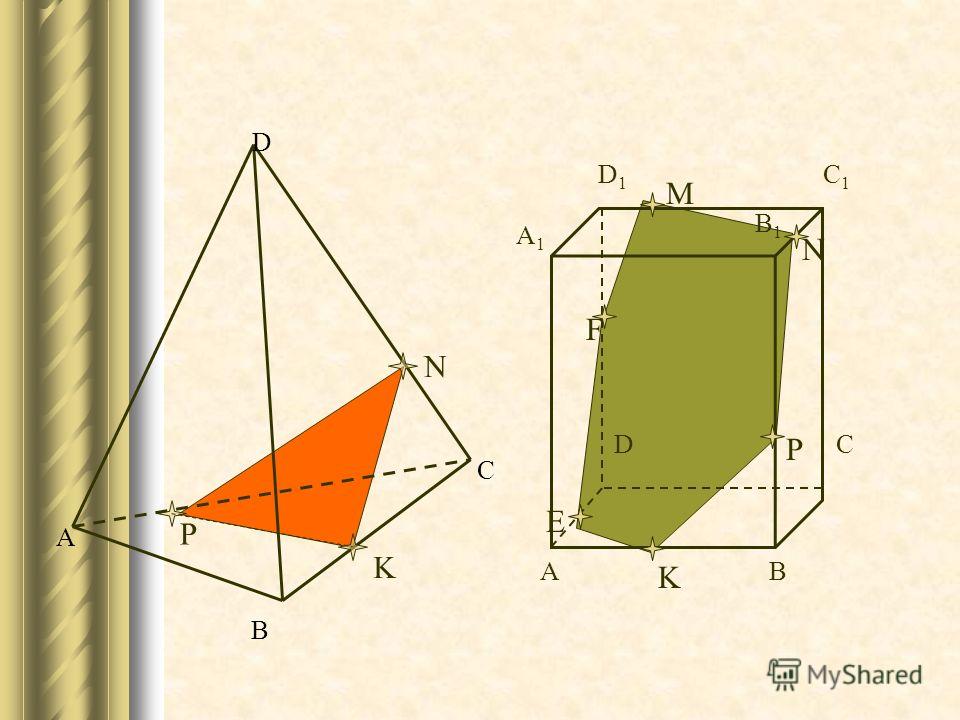
Построение:
В1
C1
1. НТ
Выберите верный вариант:
2. НТ ∩ BС = Е
А1
D1
2. НТ ∩ DС = Е
Н
Т
М
А
В
С
D
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
С
D
1. НТ
2. НТ ∩ ВС = Е
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = Е
C1
Выберите верный вариант:
А1
D1
3. ME ∩ AA1 = F
3. ME ∩ CC1 = F
3. ME ∩ BС = F
Н
Т
М
А
В
С
D
Е
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = E
3. ME ∩ AA1 = F
C1
А1
D1
Н
Т
М
А
В
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад
Задача 3.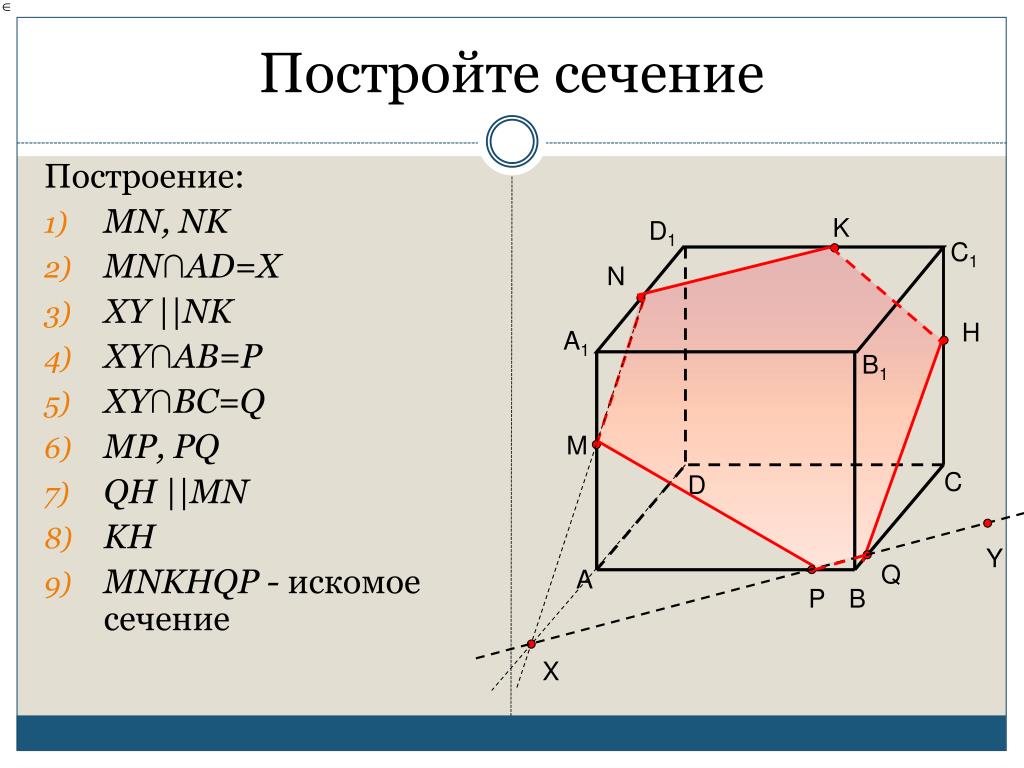 Построить сечение плоскостью,
Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
2. НТ ∩ DС = E
3. ME ∩ CC1 = F
C1
А1
D1
Н
Т
М
А
В
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
Выберите верный вариант:
D1
4. НF
Н
4. МТ
Т
М
А
В
F
С
D
4. ТF
E
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. НF
D1
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные точки
принадлежат
разным граням!
Назад
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
D1
4. MT
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные точки
принадлежат
разным граням!
Назад
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
Выберите верный вариант:
Н
5. ТF ∩ А1 А = K
Т
М
А
В
F
С
D
5. ТF ∩ В1В = K
E
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ А1 А = K
Н
Т
М
А
В
F
С
D
E
Комментарии:
Данные прямые скрещивающиеся!
Пересекаться не
могут!
Назад
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
Выберите верный вариант:
Т
6. НK ∩ АD = L
6. ТK ∩ АD = L
М
F
В
А
С
D
K
E
6. МK ∩ АА1= L
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
В1
Построение:
1. НТКомментарии:
Данные
2. НТ
∩ DС = Eпрямые скрещивающиеся!
3. ME
∩ ВС = F
Пересекаться не
4. ТF
5. ТF ∩ В1Вмогут!
=K
C1
А1
D1
Н
6. НK ∩ АD = L
Т
М
F
В
А
С
D
K
E
Назад
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
В1
Построение:
1. НТКомментарии:
Данные
2. НТ
∩ DС = Eпрямые скрещивающиеся!
3. ME
∩ ВС = F
Пересекаться не
4. ТF
5. ТF ∩ В1Вмогут!
=K
C1
А1
D1
Н
6. TK ∩ АD = L
Т
М
F
В
А
С
D
K
E
Назад
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.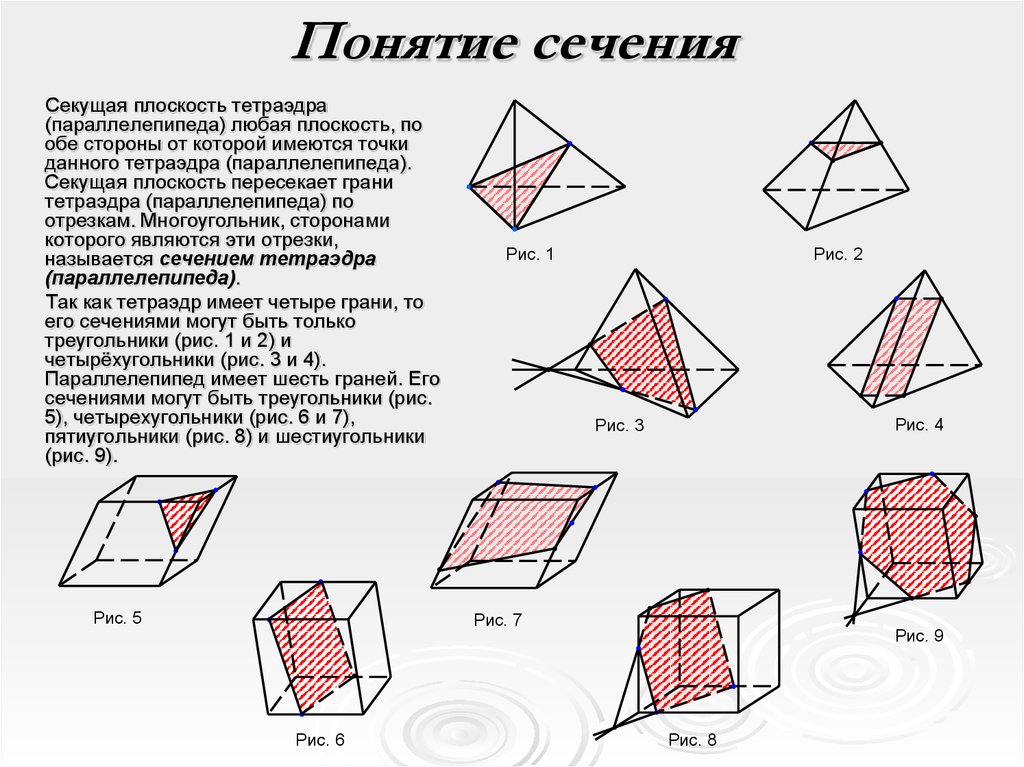
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
6. МK ∩ АА1= L
Т
Выберите верный вариант:
7. LF
М
L
F
В
А
С
D
K
E
7. LT
7. LH
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
А1
Комментарии:
3. ME ∩ ВС = F
Данные точки
4. ТF
5. ТFпринадлежат
∩ В1В = K
6. разным
МK ∩ АА1= Lграням!
D1
Н
Т
F
В
L
С
7. LТ
E
М
А
D
K
Назад
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
А1
Комментарии:
3. ME ∩ ВС = F
Данные точки
4. ТF
5. ТFпринадлежат
∩ В1В = K
6. разным
МK ∩ АА1= Lграням!
D1
Н
Т
F
В
L
С
7. LF
E
М
А
D
K
Назад
Задача 3. Построить сечение плоскостью,
Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
6. МK ∩ АА1= L
Т
F
В
L
С
М
А
D
K
7. LН
E
НТFМL – искомое сечение
Задача 4. Построить сечение плоскостью,
проходящей через данные точки Е, F, K.
Построение:
В1
F
А1
К
C1
D1
E
С
А
L
EFKNM – искомое сечение
N
В
1. KF
2. FE
3. FE ∩ АB = L
4. LN ║ FK
5. LN ∩ AD = M
6. EM
7. KN
М
Пояснения к построению:
4.
Проводим
LN параллельно FK (если
Пояснения
кпрямую
построению:
Пояснения
к построению:
Пояснения
Пояснения
кккпостроению:
построению:
секущая
плоскость
3.DПрямые
FE
и АВ,пересекает
лежащие
в принадлежащие
одной
плоскости
Пояснения
построению:
1. Соединяем
2.
точки
K и E,
F
F,
принадлежащие
7.
6.
Соединяем
точки
точкиграни,
КЕииN,
М,ребро
принадлежащие
принадлежащие
противоположные
она
пересекает
их
АА1В1одной
В,LN
пересекаются
вАА
L .в точке M.
5.Соединяем
Прямая
пересекает
AD
плоскости то
А1точке
В1В
1С
1В.
1D1.
одной
одной
плоскости
плоскости ВСС
АА
по параллельным
отрезкам).
1D
1В
1D.
1.
Задача 5. Построить сечение плоскостью, проходящей
через данные точки К, М, Р, Р∈АВС
Построение:
1. КМ
2. КМ ∩ СА = Е
3. EР
4. ЕР ∩ АВ = F
ЕР ∩ ВC = N
5. МF
6. NК
КМFN – искомое сечение
S
К
М
Е
А
F
С
Р
N
В
Задача 6. Построить сечение плоскостью,
проходящей через точки К, L, М.
Построение:
T
К
В1
C1
F
E
А1
L
А
D1
В
P
С
G
D
М
N
1. ML
ML
2. ML ∩ D1А1 = E
3. EK
4. EK ∩ А1B1 = F
5. LF
6. LM ∩ D1D = N
7. ЕK ∩ D1C1 = T
8. NT
9. NT ∩ DC = G
NT ∩ CC1 = P
10. MG
11. PK
МLFKPG – искомое сечение
Задача 7. Построить сечение плоскостью,
проходящей через данные точки F, K, L.
В1
К
А1
C1
D1
L
В
С
А
F
D
Задача 7. Построить сечение плоскостью,
проходящей через данные точки F, K, L.
Проверка:
В1
М
А1
К
C1
D1
L
В
N
С
FМKLN – искомое сечение
А
F
D
Геометрия поперечного сечения
Скачать страницу Геометрия поперечного сечения.
Геометрия границ для анализа течения в естественных водотоках определяется в терминах профилей земной поверхности (поперечных сечений) и измеренных расстояний между ними (длины досягаемости). Поперечные сечения расположены с интервалами вдоль ручья, чтобы охарактеризовать пропускную способность ручья и прилегающей к нему поймы. Они должны проходить через всю пойму и должны быть перпендикулярны ожидаемым линиям потока. Иногда для выполнения этого требования необходимо расположить поперечные сечения по криволинейной или изогнутой линии. Необходимо приложить все усилия для получения поперечных сечений, точно отображающих геометрию ручья и поймы.
Они должны проходить через всю пойму и должны быть перпендикулярны ожидаемым линиям потока. Иногда для выполнения этого требования необходимо расположить поперечные сечения по криволинейной или изогнутой линии. Необходимо приложить все усилия для получения поперечных сечений, точно отображающих геометрию ручья и поймы.
Пример размещения поперечных сечений показан ниже на рисунке ниже. Общий подход к размещению поперечных сечений заключается в обеспечении того, чтобы поперечные сечения были перпендикулярны линиям потока. Это требует оценки того, как будут выглядеть линии потока в прибрежных районах вдали от основного русла. Один из вариантов — провести осевую линию потока вниз по основному каналу вдоль того места, которое воспринимается как центр массы потока. То же самое нужно сделать для левого и правого берегов. Предполагаемые пути потока для русла и береговых зон показаны пунктирными линиями на рисунке ниже. Эти линии не только помогут в построении поперечных сечений, перпендикулярных линиям потока, но также представляют путь для измерения длин досягаемости между поперечными сечениями.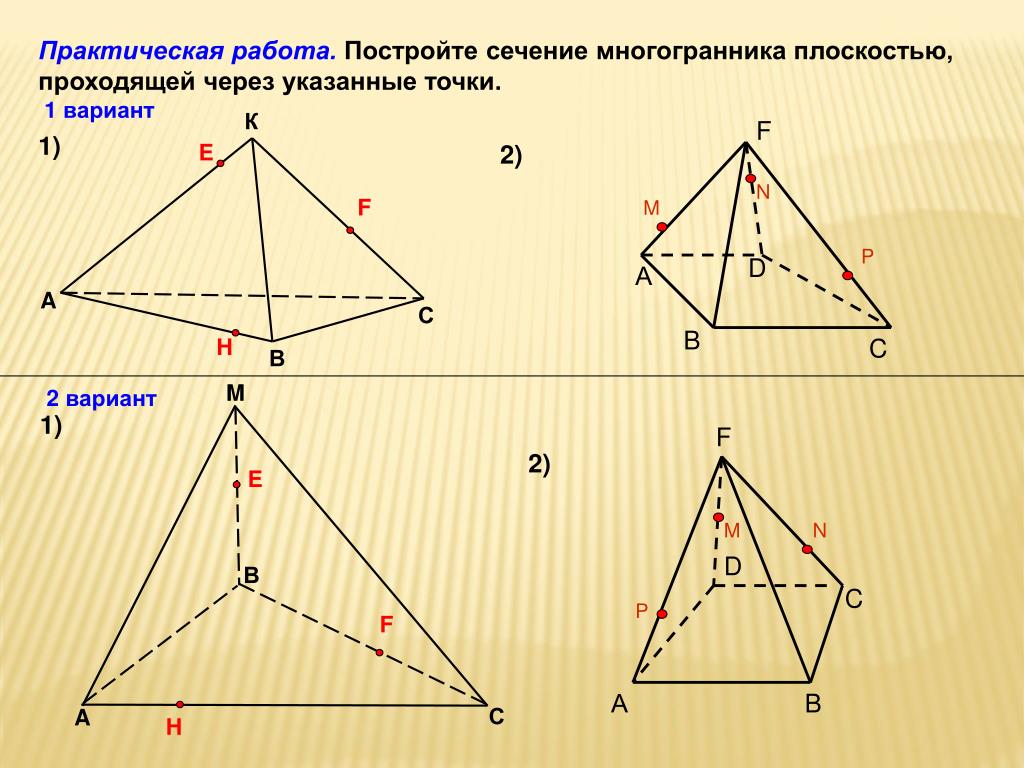
Поперечные сечения требуются в репрезентативных местах по всему участку ручья и в местах, где происходят изменения расхода, уклона, формы или шероховатости, в местах, где начинаются или заканчиваются дамбы, а также на мостах или регулирующих сооружениях, таких как плотины. Там, где происходят резкие изменения, следует использовать несколько поперечных сечений для описания изменения независимо от расстояния. Расстояние поперечного сечения также зависит от размера потока, уклона и однородности формы поперечного сечения. Как правило, для больших однородных рек с плоским уклоном обычно требуется наименьшее количество поперечных сечений на милю. Цель исследования также влияет на расстояние между поперечными сечениями. Например, навигационные исследования на больших относительно плоских потоках могут потребовать близко расположенных (например, 200 футов) поперечных сечений для анализа влияния местных условий на малые глубины потока, в то время как поперечные сечения для исследований наносов для определения отложений в водохранилищах могут быть разнесены друг от друга.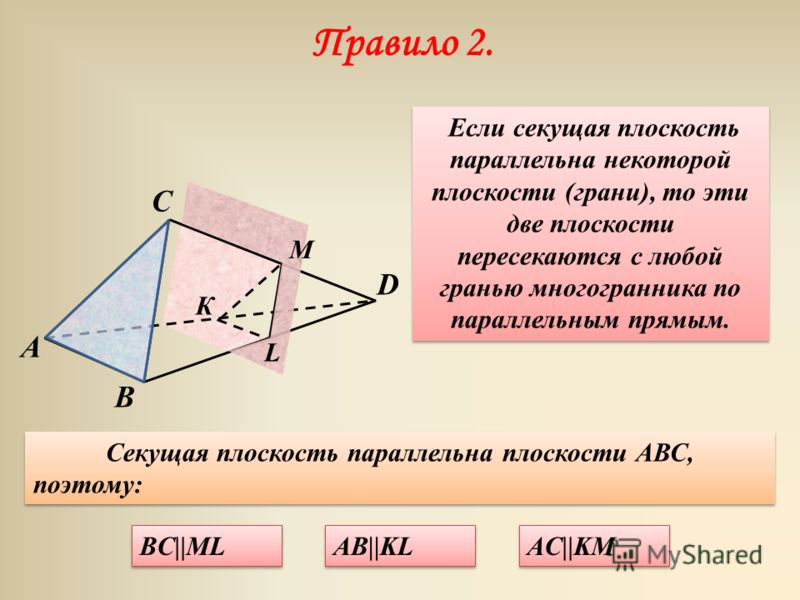 с интервалами порядка тысячи футов.
с интервалами порядка тысячи футов.
Выбор уравнения потерь на трение также может влиять на расстояние между поперечными сечениями. Например, расстояние между поперечными сечениями может быть максимальным при расчете профиля М1 (профиль подпора) с помощью уравнения среднего коэффициента трения или когда уравнение среднего гармонического коэффициента трения используется для расчета профилей М2 (профиль просадки). Программное обеспечение HEC-RAS позволяет программе выбрать уравнение усреднения.
Каждый поперечный разрез в наборе данных HECRAS идентифицируется меткой реки, участка и речной станции. Поперечное сечение описывается путем ввода станции и высоты (данные X-Y) слева направо, если смотреть вниз по течению. Идентификатор речной станции может соответствовать стоянке вдоль канала, милям или любой фиктивной системе нумерации. Система нумерации должна быть согласованной, поскольку программа предполагает, что более высокие числа относятся к восходящему потоку, а меньшие — к нисходящему.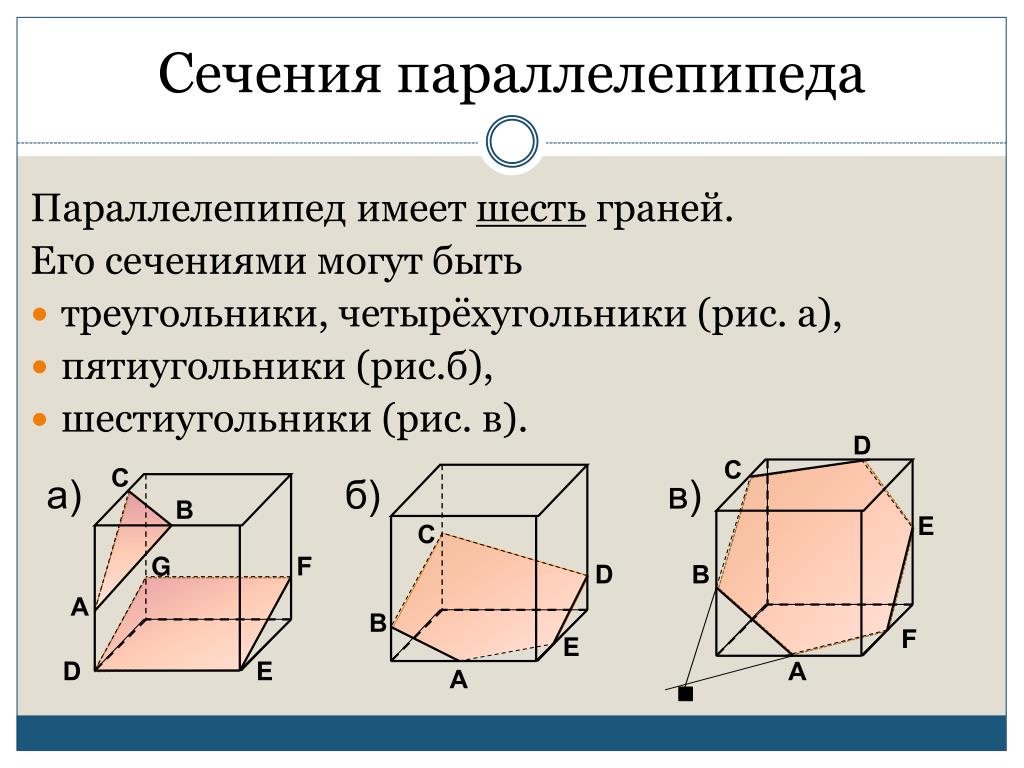
Каждой точке данных в поперечном сечении присваивается номер станции, соответствующий горизонтальному расстоянию от начальной точки слева. Для описания каждого поперечного сечения может использоваться до 500 точек данных. Данные поперечного сечения традиционно определяются в направлении вниз по течению. Программа считает, что левая сторона потока имеет наименьшие номера станций, а правая — самые высокие. Данные поперечного сечения могут иметь отрицательные значения пикетирования. Размещение необходимо вводить слева направо в порядке возрастания. Однако одно и то же значение пикетажа может иметь более одной точки. Левый и правый пикеты, отделяющие основное русло от береговых участков, должны быть указаны в редакторе данных разреза. Слишком низкие конечные точки поперечного сечения (ниже расчетной отметки поверхности воды) будут автоматически расширены по вертикали, и в выходных данных для этого сечения появится примечание, указывающее, что поперечное сечение необходимо расширить.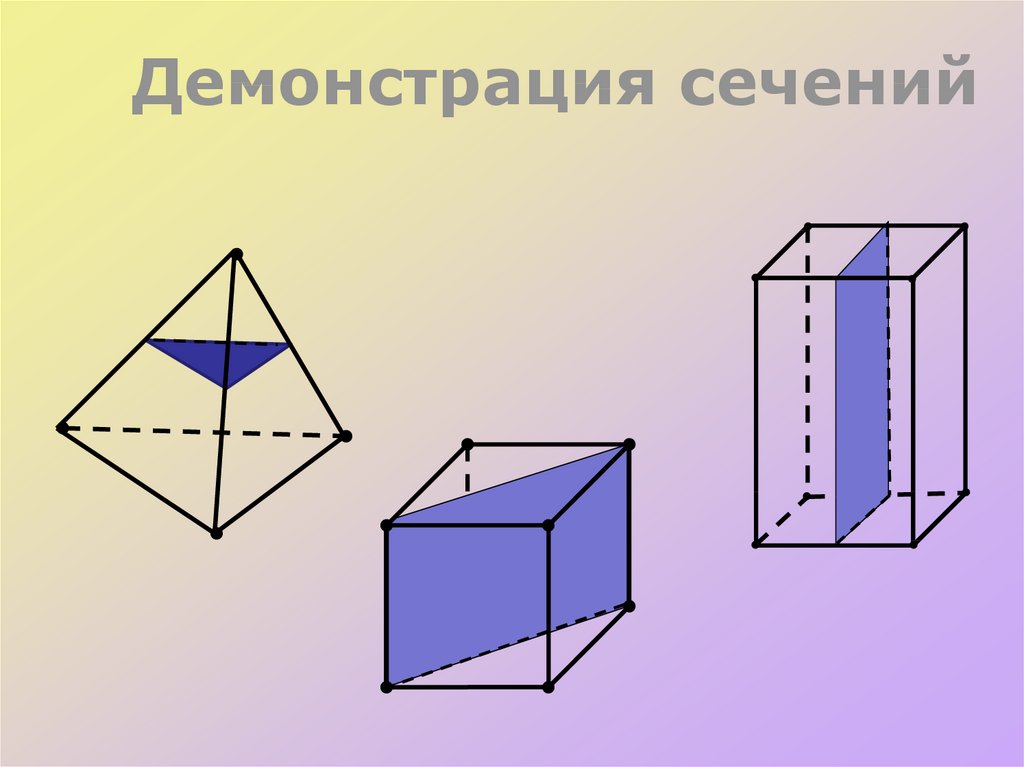 Программа добавляет дополнительный смачиваемый периметр для любой воды, которая вступает в контакт с расширенными стенами.
Программа добавляет дополнительный смачиваемый периметр для любой воды, которая вступает в контакт с расширенными стенами.
Другие данные, которые требуются для каждого поперечного сечения, включают: длину участка вниз по течению; коэффициенты шероховатости; коэффициенты сжатия и расширения. Эти данные будут подробно рассмотрены далее в этой главе.
Доступны многочисленные опции программы, позволяющие пользователю легко добавлять или изменять данные поперечного сечения. Например, когда пользователь хочет повторить съемку поперечного сечения, в интерфейсе доступна опция создания копии любого поперечного сечения. После копирования поперечного сечения доступны другие параметры, позволяющие пользователю изменять горизонтальные и вертикальные размеры повторяющихся данных поперечного сечения. Подробное объяснение того, как использовать эти параметры поперечного сечения, см. в разделе «Моделирование водопропускных труб» руководства пользователя HEC-RAS.
алгебраическая геометрия — что такое «раздел»?
спросил
Изменено
4 года, 7 месяцев назад
Просмотрено
957 раз
$\begingroup$
Я прочитал 4 главы «Алгебраической геометрии» Хартсхорна, когда я возвращаюсь к началу схемы и определению сечения, я немного смущен, почему мы называем такой элемент «сечением».
Приведу определение: если $\mathcal{F}$ — предпучок, мы называем $\mathcal{F}(U)$ сечения предпучка $\mathcal{F}$ над открытым множеством $U $.
В случае структурного пучка (на многообразии или аффинной схеме) мы называем $\mathcal{O}(U)$ множество (регулярных) функций. А как насчет других пучков? Как я должен рассматривать эти «разделы» как? (функции? рациональные функции? карты?) Когда эти разделы могут стать рациональными функциями?
(В базовой алгебре для короткой точной последовательности $0\to A\to B\to C\to 0$ «сечением» является отображение $C\to B$ такое, что композиция $C\to B\ в C$ есть тождество. Имеют ли в алгебраической геометрии эти «сечения» сходное свойство?)
Приветствуется любая точка зрения! Большое спасибо!
- алгебраическая геометрия
$\endgroup$
1
$\begingroup$
Происхождение терминологии, я думаю, происходит от пучков в топологии.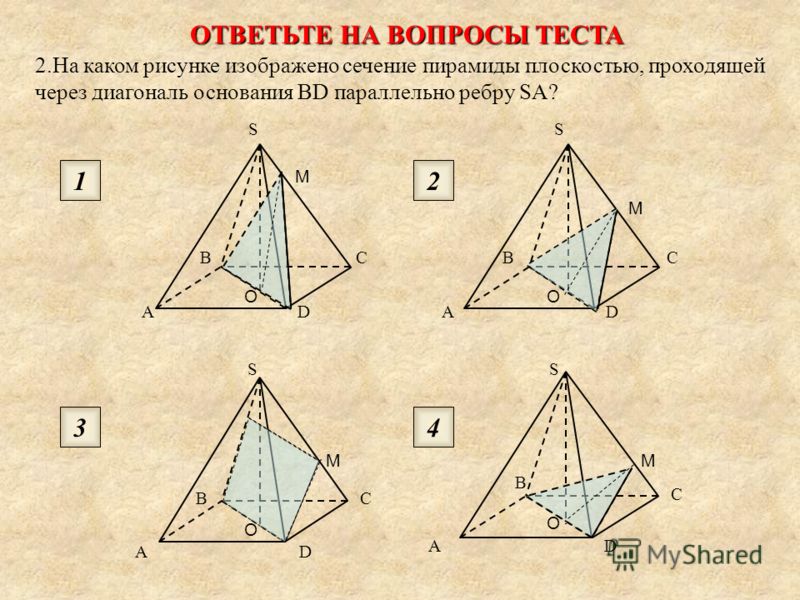 Для заданного базового пространства $B$ и расслоения над $B$, т. е. непрерывного отображения $E \xrightarrow{\pi} B$, сечением этого расслоения является непрерывное отображение $s : B \to E$ с $\pi \circ s = 1_B$.
Для заданного базового пространства $B$ и расслоения над $B$, т. е. непрерывного отображения $E \xrightarrow{\pi} B$, сечением этого расслоения является непрерывное отображение $s : B \to E$ с $\pi \circ s = 1_B$.
Это определение имеет очевидное обобщение на очень произвольные ситуации; например определение, которое вы цитируете из базовой алгебры.
В более общем случае мы можем рассматривать локальных разделов; для заданного открытого подмножества $U \subseteq B$ сечением расслоения $E \xrightarrow{\pi} B$ над $U$ называется непрерывное отображение $s : U \to E$ такое, что $\pi \circ s $ — отображение включения $U \to B$.
С каждым пучком множеств $F$ на топологическом пространстве $B$ связано этальное пространство : расслоение $E_F \xrightarrow{\pi} B$, обладающее тем свойством, что $F(U)$ естественно изоморфно множеству сечений над $U$ этого расслоения.
На самом деле категория пучков множеств на $B$ эквивалентна категории расслоений на $B$, для которых $\pi$ является локальным гомеоморфизмом .

 Треугольник АЕС, сторонами которого являются эти отрезки, называется сечением тетраэдра.
Треугольник АЕС, сторонами которого являются эти отрезки, называется сечением тетраэдра.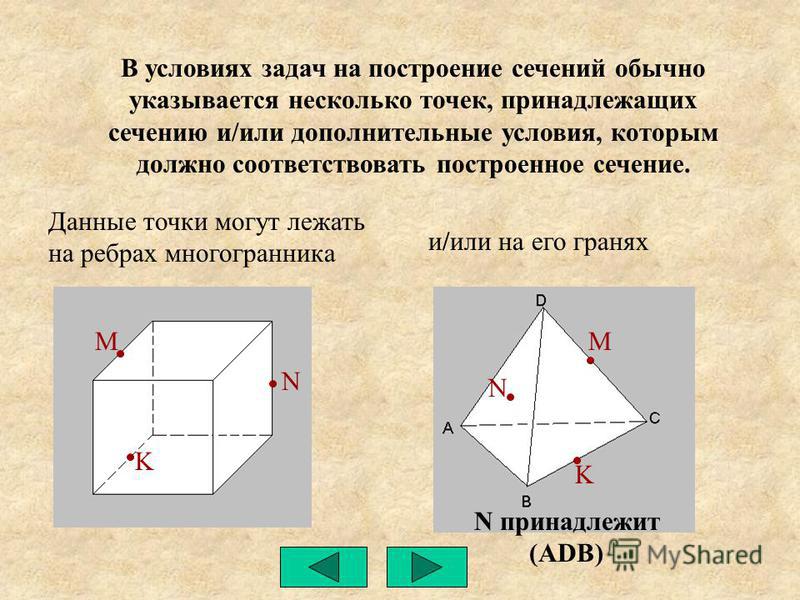 Отрезки образуют многоугольник, который называется сечением параллелепипеда.
Отрезки образуют многоугольник, который называется сечением параллелепипеда.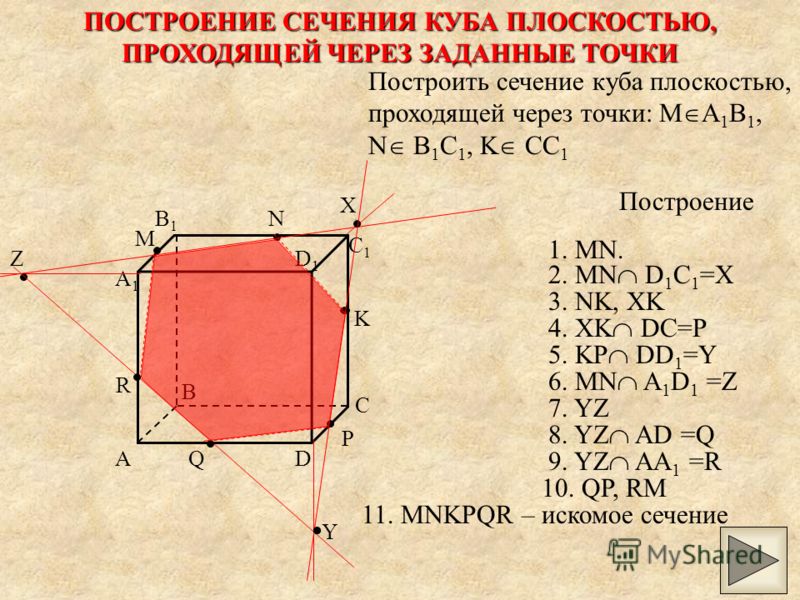 Значит, отрезок АВ и отрезок RP на чертеже должны быть изображены параллельно. А мы наблюдаем, что это не так . Но и отрезки AR и BP тоже не параллельны, хотя лежат в параллельных плоскостях. Значит плоскость α, должна пересекать грани АА1D1D и BB1C1C по параллельным прямым.
Значит, отрезок АВ и отрезок RP на чертеже должны быть изображены параллельно. А мы наблюдаем, что это не так . Но и отрезки AR и BP тоже не параллельны, хотя лежат в параллельных плоскостях. Значит плоскость α, должна пересекать грани АА1D1D и BB1C1C по параллельным прямым.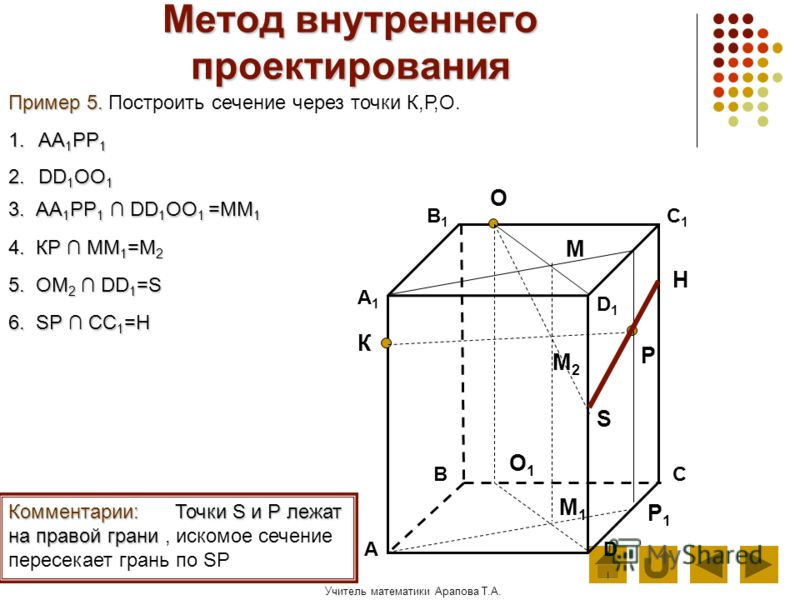
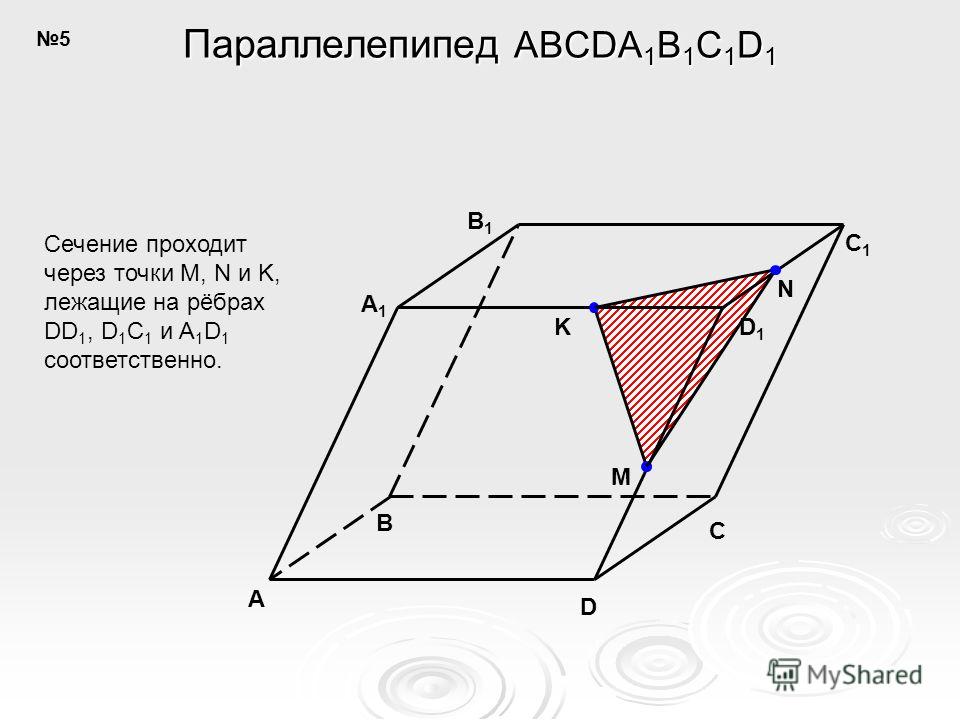 Точка М уже у нас есть.
Точка М уже у нас есть.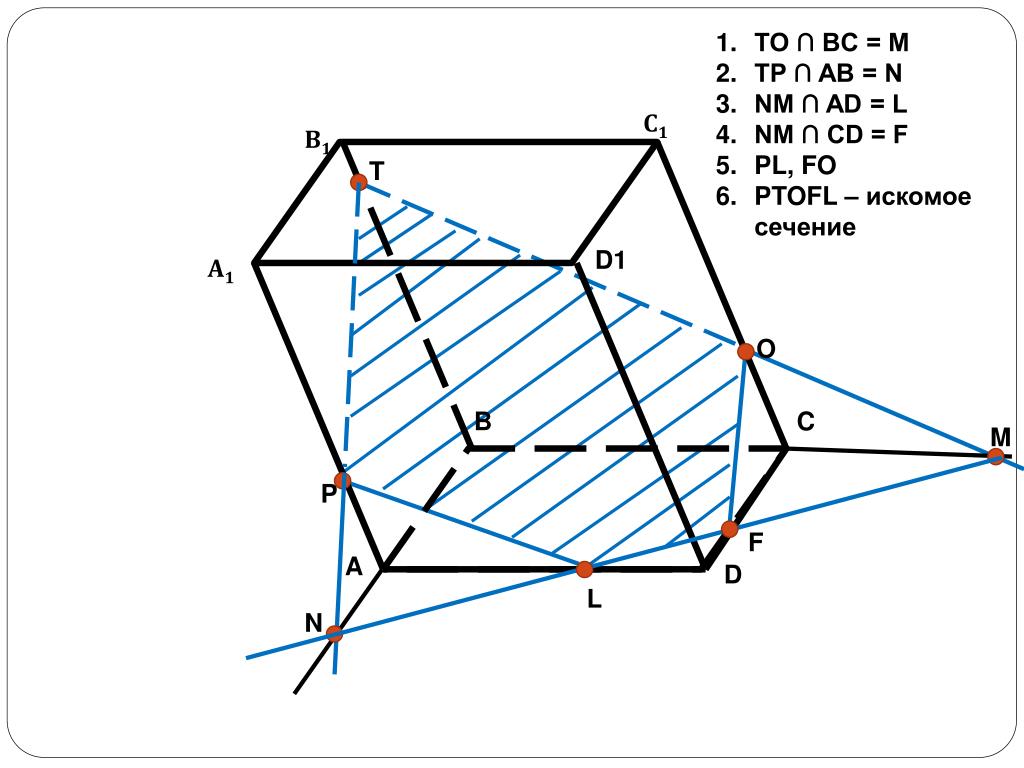 Отрезок КР есть линия пересечения секущей плоскости и грани. Проведем этот отрезок.
Отрезок КР есть линия пересечения секущей плоскости и грани. Проведем этот отрезок.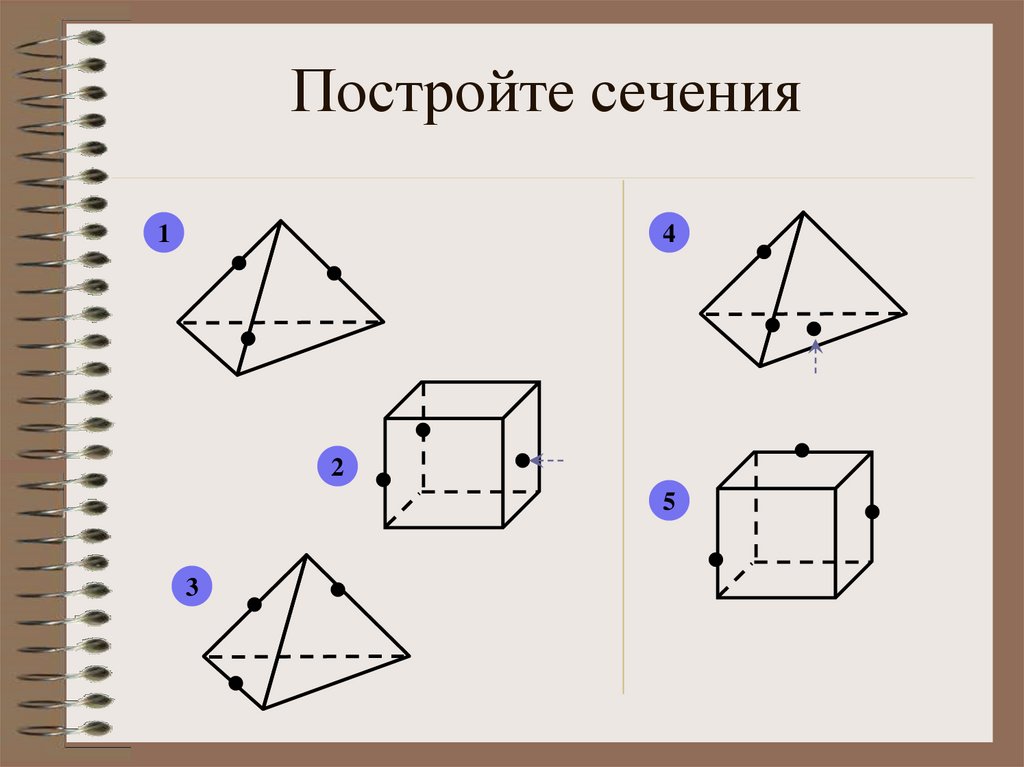
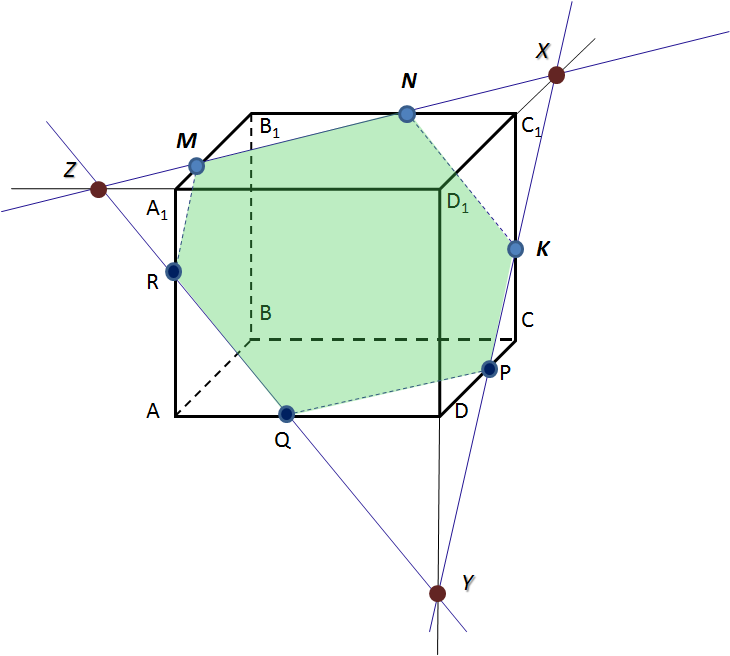 И принадлежит грани A1B1C1D1, так как принадлежит прямой D1C1. Проведем прямую LH. Отметим точку T точку пересечения прямой с ребром B1C1. Выделим отрезок LT это будет след от сечения плоскость.
И принадлежит грани A1B1C1D1, так как принадлежит прямой D1C1. Проведем прямую LH. Отметим точку T точку пересечения прямой с ребром B1C1. Выделим отрезок LT это будет след от сечения плоскость.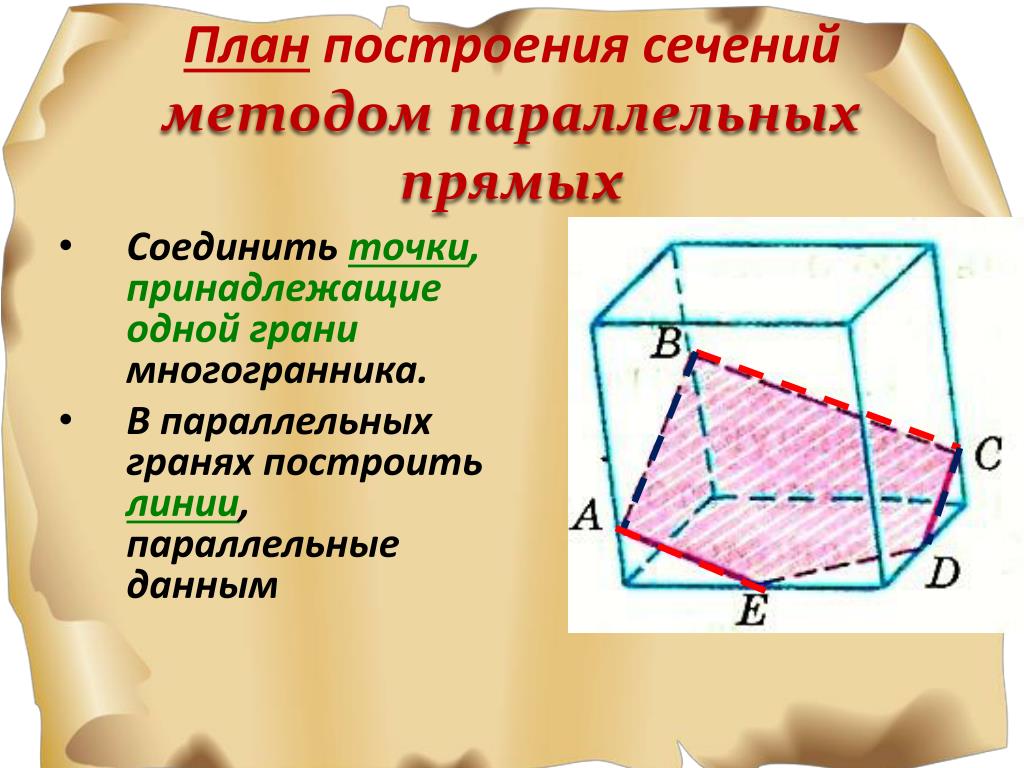 Мы рассмотрели только этап построения, так как наша цель– научиться строить искомое сечение.
Мы рассмотрели только этап построения, так как наша цель– научиться строить искомое сечение.