Уклон линии что такое: § 13. Уклон линии. Определение уклонов по горизонталям. Определение высот точек, лежащих между горизонталями
Содержание
Билет №14. Определение уклонов и углов наклона по карте. Построение линии заданного уклона — Мегаобучалка
Определение уклонов и углов наклона. Отрезки линий на земной поверхности обычно имеют наклон, отчего начало и конец отрезка находятся на разных высотах. Разность их высот – превышение, а проекция отрезка на горизонтальную плоскость – его горизонтальное проложение.
Уклоном i линии называется отношение превышения h к горизонтальному проложению d:
i = h / d. (4.2)
Для определения по карте уклона линии на участке KL между двумя горизонталями (рис. 4.7) измеряют его горизонтальное проложение – заложение d. Поскольку концы отрезка лежат на смежных горизонталях, превышение hмежду ними равно высоте сечения рельефа, подписанному под южной рамкой карты. Воспользовавшись формулой (4.2), вычисляют уклон, который принято выражать в тысячных. Если, например, h=1 м, d=48 м , то уклон равен i =1 м / 48 м = 0,021=21‰.
|
Рис. 4.7. Определение высоты точки M и уклона на отрезке KL |
С другой стороны, отношение превышения h к горизонтальному проложению d равно тангенсу угла n наклона линии. Поэтому
i =tg n,
что позволяет, вычислив уклон определить по нему угол наклона.
При пользовании картой углы наклона не вычисляют, а определяют с помощью графика заложений (рис. 4.8), расположенного под южной рамкой карты. По горизонтальной оси графика отложены углы наклона, а по вертикальной — соответствующие этим углам заложения d, выраженные в масштабе карты и рассчитанные по формуле
d = h¤(Mtg n),
гдеh — высота сечения рельефа, а M – знаменатель масштаба карты.
|
Рис. 4.8. График заложений |
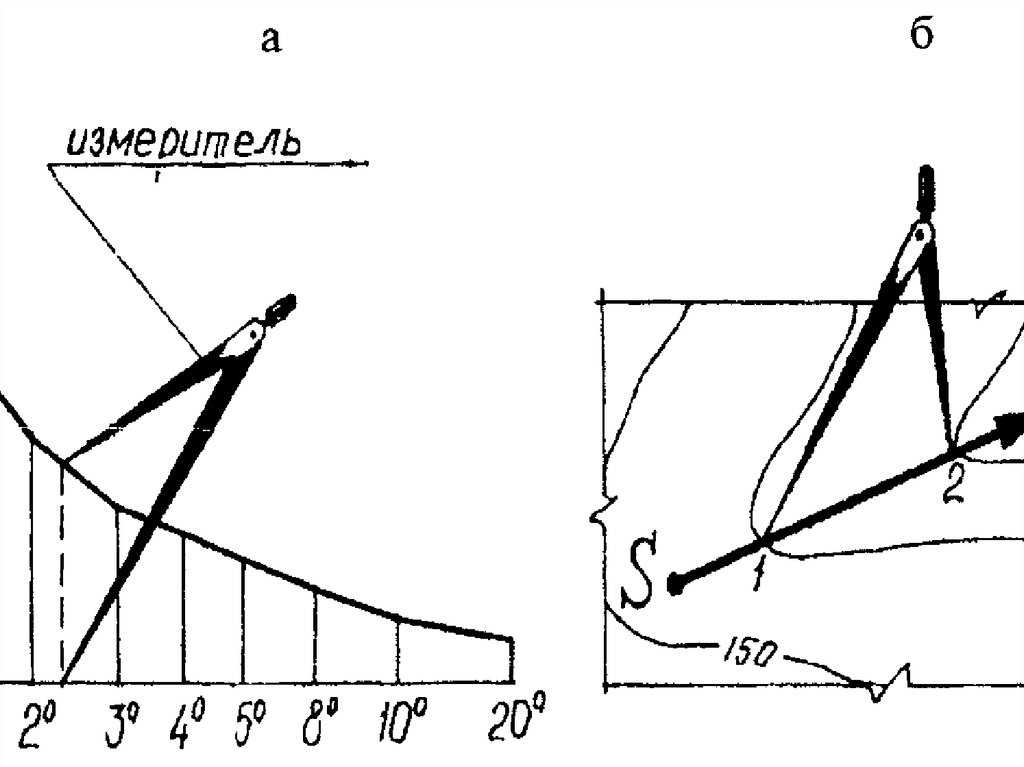
Для определения угла наклона отрезка KL (рис.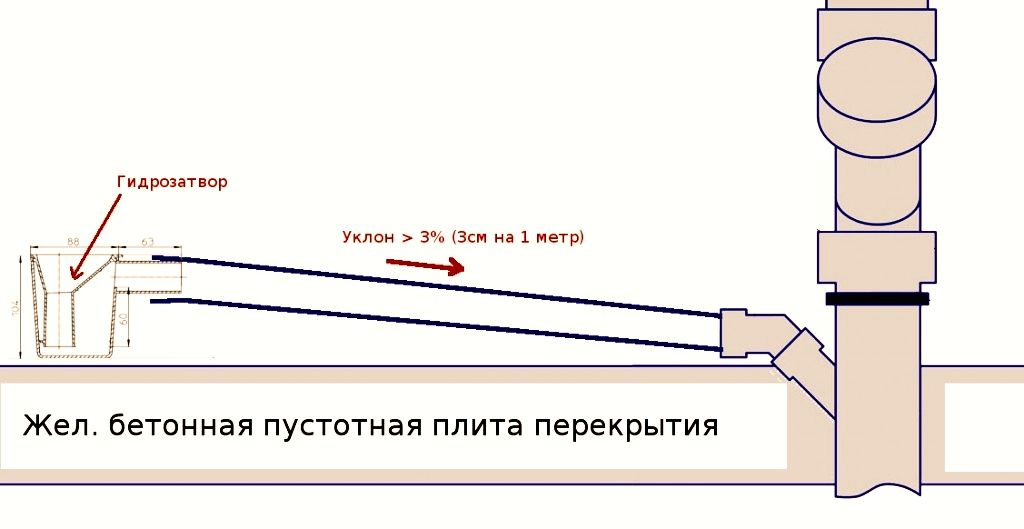 4.7), расположенного между горизонталями, берут его в раствор циркуля и на графике заложений (рис. 4.8) находят такой угол, над которым ордината равна раствору циркуля d. Это и есть искомый угол наклона.
4.7), расположенного между горизонталями, берут его в раствор циркуля и на графике заложений (рис. 4.8) находят такой угол, над которым ордината равна раствору циркуля d. Это и есть искомый угол наклона.
При необходимости многократного определения уклонов пользуются графиком уклонов, построенным аналогично графику заложений, но с отложением по горизонтальной оси не углов наклона, а уклонов.
Проведение линии с уклоном, не превышающим заданного предельного. Необходимость решения такой задачи возникает, например, при выборе трассы для будущей дороги. Вычисляют соответствующее заданному предельному уклону iпр заложение, выраженное в масштабе карты, (здесь M – знаменатель масштаба). .
| Рис. 4.9. Построение линии с заданным уклоном | Рис. 4.10. Водосборная площадь |
Чтобы уклон линии не превосходил iпр, ни одно заложение на ней не должно быть меньше, чем рассчитанное d. Если расстояние между горизонталями больше рассчитанного, направление линии можно выбирать произвольно. В противном случае в раствор циркуля берут отрезок, равный d, и строят ломаную линию, умещая между горизонталями рассчитанное предельное заложение (рис. 4.9).
Если расстояние между горизонталями больше рассчитанного, направление линии можно выбирать произвольно. В противном случае в раствор циркуля берут отрезок, равный d, и строят ломаную линию, умещая между горизонталями рассчитанное предельное заложение (рис. 4.9).
Проектный уклон — это… Что такое Проектный уклон в геодезии, определение
Превышение — То же, что относительная высота.
Профиль — Вертикальное сечение, разрез какого-либо участка земной поверхности, земной коры, гидросферы или атмосферы по заданной линии.
Пикет — Точка на местности (обозначенная знаком), служащая ориентиром для установки рейки при нивелировании и для закрепления трассы на местности. Закрепляет заданный интервал.
План — 1) Чертеж, изображающий в условных знаках на плоскости (в масштабе 1:10 000 и крупнее) часть земной поверхности (топографический план) и построенный без учета кривизны Земли.
2) Горизонтальный разрез или вид сверху какого-либо сооружения или предмета.
3) То же, что горизонтальная проекция.
Пятка рейки — Основание рейки, предназначенное для установки ее на репер, башмак или костыль.
Палетка — Прозрачная пластинка с нанесенной на нее сеткой линий (реже — точек), предназначенная для вычисления площадей на планах и картах, отсчета координат и т. д.
Планшет — 1) Часть мензулы, квадратная деревянная доска (размер стороны от 40 до 70 см), на которую наклеивается чертежная бумага. 2) Дощечка или папка, на которой укрепляются компас и бумага при глазомерной съемке.
Параллель — Линия сечения поверхности земного шара плоскостью, параллельной плоскости экватора. Все точки этой линии имеют одинаковую широту.
Привязка геодезическая — Интеграция (объединение) новых геодезических данных с ранее созданными.
Проектная линия — Линия, определяющая положение сооружений в плане и по высоте.
Пространственные данные — Цифровые данные о пространственных объектах, включающие сведения об их местоположении, форме и свойствах, представленные в координатно–временной системе.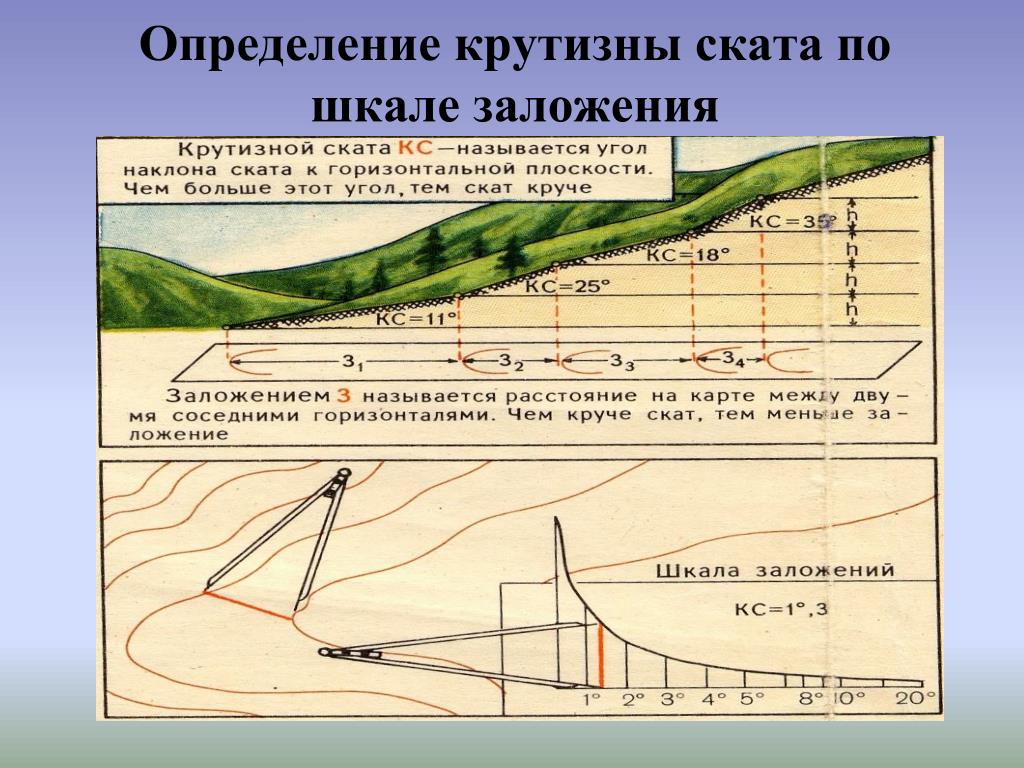
Параллакс — Видимое изменение положение предмета (тела) вследствие перемещения глаза наблюдателя.
Полигонометрический пункт — Геодезический пункт, координаты которого определены методом полигонометрии, а положение на местности обозначено металлическими столбами или бетонными монолитами.
Пеленг — Угол между направлением на наблюдаемый объект и одной из основных плоскостей, принятых за начало отсчета угловых координат. В морской и воздушной навигации обычно то же, что азимут.
Полигонометрия — Метод построения геодезической сети в форме ломаной линии, в которой измеряют все стороны и углы.
Первый вертикал — Плоскость перпендикулярная к меридиану.
Постобработка (спутниковых наблюдений) — Окончательная обработка данных в камеральных условиях с целью получения координат пунктов.
Планиметр — Механическое или электронное устройство для измерения площадей объектов по планам и картам.
Пантометр — Угломерный геодезический инструмент, применявшийся при съемке лесов и торфяных болот.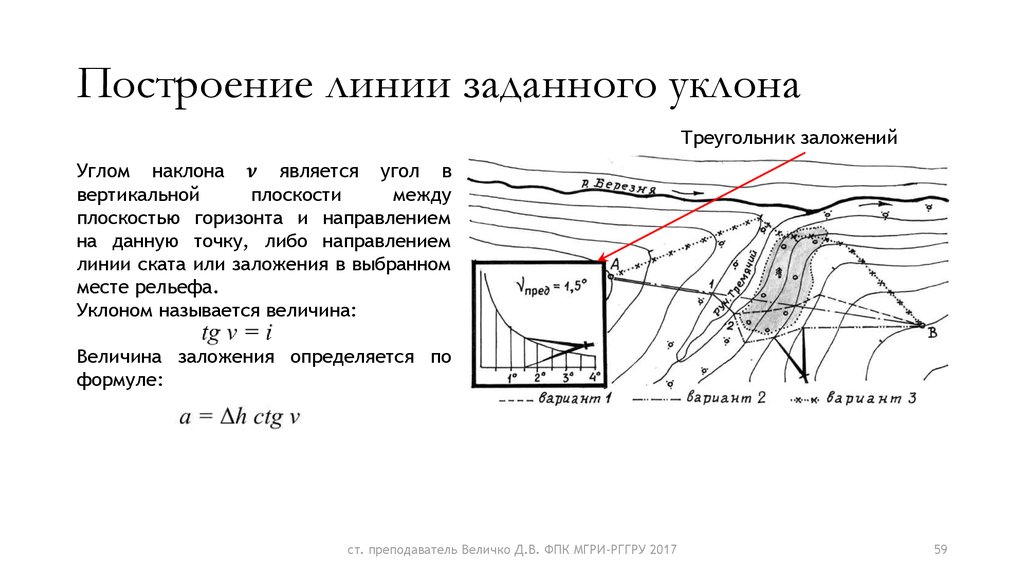
Прямая геодезическая задача — Вычисление геодезических координат — широты и долготы некоторой точки, лежащей на земном эллипсоиде, по координатам другой точки и по известным длине и дирекционному углу данного направления, соединяющей эти точки.
Полевое трассирование — Перенос запроектированной трассы на местность с уточнением ее изменения и закрепление в натуре.
Плоскогорье — Обширный участок земной поверхности, представляющий собой горную равнину, характеризующуюся значительным эрозионным расчленением.
Произвольные проекции — Картографические проекции, искажающие углы и площади. Выделяются равнопромежуточные, сохраняющие масштаб длин по одному из направлений (например, по меридианам или параллелям), и ортодромические, в которых большие круги шара (ортодромы) изображаются прямыми. Применяются для карт мира.
Полярные координаты — Система плоских координат образованная направленным прямым лучом OX, называющимся полярной осью. Чаще всего за полярную ось принимают ось северного направления какого-либо меридиана. Начало координат — точка O — называется полюсом системы.
Чаще всего за полярную ось принимают ось северного направления какого-либо меридиана. Начало координат — точка O — называется полюсом системы.
Перекрытие снимка — В фотограмметрии, доля площади снимка (аэроснимка), перекрываемая смежным снимком.
Прямоугольные координаты — Система плоских координат образованная двумя взаимноперпендикулярными прямыми линиями, называемыми осями координат x и y. Точка их пересечения называется началом или нулем системы координат. Ось абсцисс – OX, ось ординат – OY.
Плановая аэрофотосъемка — Фотографирование местности при положении оптической оси аэрофотоаппарата, близком к вертикальному.
Плановая разбивочная основа — Геодезическое построение на строительной площадке, обеспечивающее взаимную увязку всех проектных элементов комплекса и служащее для получения исходных данных для выноса в натуру.
Пеленгация — Определение направления на какой-либо объект — его угловых координат. Осуществляется оптическими, радиотехническими, акустическими и другими методами.
Пункт геодезический — Закрепленная на местности точка геодезической сети.
Перспективная аэрофотосъемка — Фотографирование местности аэрофотоаппаратом, оптическая ось которого отклонена от вертикали на некоторый постоянный угол.
Погрешности измерений — Отклонение результата геодезических измерений от истинного (действительного) значения измеряемой геодезической величины.
Поликонические проекции — Картографические проекции, параллели которых — дуги эксцентрических окружностей, а меридианы — кривые, симметричные относительно среднего прямолинейного меридиана. Применяются для карт мира.
Полюсы магнитные Земли — Точки на земной поверхности, где магнитная стрелка располагается по вертикали, т. е. где магнитный компас неприменим для ориентировки по странам света.
Палеогеографические карты — Отображают физико-географические условия геологического прошлого (распределение суши, моря и речной сети, характер рельефа материков, климатические особенности и т. п.).
п.).
Наклон – определение, типы, примеры
Наклон линии – это мера крутизны и направления линии. Нахождение наклона линий на координатной плоскости может помочь предсказать, параллельны ли линии, перпендикулярны или нет, без фактического использования компаса.
Наклон любой линии можно рассчитать, используя любые две различные точки, лежащие на линии. Формула наклона линии вычисляет отношение «вертикального изменения» к «горизонтальному изменению» между двумя различными точками на линии. В этой статье мы разберемся с методом нахождения уклона и его применениями.
| 1. | Что такое уклон? |
| 2. | Наклон линии |
| 3. | Наклон линии Формула |
| 4. | Как найти уклон? |
| 5. | Типы уклонов |
| 6. | Наклон перпендикулярных линий |
7. | Наклон параллельных линий |
| 8. | Часто задаваемые вопросы о склоне |
Что такое уклон?
Наклон линии определяется как изменение координаты y по отношению к изменению координаты x этой линии . Чистое изменение координаты y равно Δy, а чистое изменение координаты x равно Δx. Таким образом, изменение координаты y по отношению к изменению координаты x можно записать как
м = Δy/Δx
где м — уклон
Обратите внимание, что тангенс θ = Δy/Δx
Мы также называем этот тангенс θ наклоном линии.
Наклон линии
Наклон линии представляет собой отношение подъема к пробегу или подъема, деленное на пробег. Он описывает крутизну линии в координатной плоскости. Вычисление наклона линии аналогично нахождению наклона между двумя разными точками. В общем, чтобы найти наклон линии, нам нужно иметь значения любых двух разных координат на линии.
Наклон между двумя точками
Наклон линии можно рассчитать, используя две точки, лежащие на прямой. Зная координаты двух точек, мы можем применить формулу наклона линии. Пусть координаты этих двух точек будут
.
Р 1 = (х 1 , у 1 )
P 2 = (x 2 , y 2 )
Как мы обсуждали в предыдущих разделах, наклон представляет собой «изменение координаты y по отношению к изменению координаты x этой линии». Итак, подставляя значения Δy и Δx в уравнение наклона, мы знаем, что:
Δу = у 2 — у 1
Δx = x 2 — x 1
Следовательно, используя эти значения в соотношении, мы получаем: — x 1 )
где m — наклон, а θ — угол, образуемый линией с положительной осью x.
Формула наклона линии
Наклон линии можно рассчитать по уравнению линии. Общий наклон формулы линии задается как
y = mx + b
где
- м — уклон, такой, что m = tan θ = Δy/Δx
- θ — угол, образуемый линией с положительной осью x
- Δy — чистое изменение по оси Y
- Δx — чистое изменение по оси x
Наклон линии Пример
Вспомним определение наклона линии и попробуем решить приведенный ниже пример.
Пример: Уравнение линии с наклоном 1, проходящей через точку (-1, -5) ?
Решение:
Мы знаем, что если уклон равен 1, то значение м будет равно 1 в общем уравнении y = mx + b. Итак, подставляем значение м в 1, и получаем
y = x + b
Теперь у нас уже есть значение одной точки на прямой. Итак, подставляем значение точки (-1, -5) в уравнение y = x + b, и получаем,
b = -4
Отсюда, подставляя значения m и b в общем уравнении, мы получаем наше окончательное уравнение как y = x — 4.
Уравнение: y = x — 4
Как найти уклон?
Наклон линии можно найти разными способами. Первый метод определения значения уклона заключается в использовании уравнения, которое задается следующим образом:
где m — наклон линии.
Кроме того, изменение x равно запустить и изменить y рост или падение . Таким образом, мы также можем определить наклон как m = подъем/спуск
Таким образом, мы также можем определить наклон как m = подъем/спуск
Нахождение наклона на графике
Один из методов нахождения наклона линии на графике заключается в непосредственном применении формулы с учетом координат двух лежащих точек. на линии. Допустим, значения координат двух точек не заданы. Итак, у нас есть еще один способ найти наклон линии. В этом методе мы пытаемся найти тангенс угла, образованного линией с осью x. Следовательно, мы находим наклон, как указано ниже.
Наклон линии имеет только одно значение. Таким образом, наклоны, найденные методами 1 и 2, будут равны. В дополнение к этому, скажем, нам дано уравнение прямой линии. Общее уравнение линии может быть дано как
y = mx + b
Значение уклона дано как м; , следовательно, значение м дает наклон любой прямой.
Следующие шаги можно выполнить, чтобы найти наклон прямой, такой, что координаты двух точек, лежащих на прямой, равны: (2, 4), (1, 2)
- Шаг 1: Запишите координаты двух точек, лежащих на прямой, (x 2 , y 2 ), (x 1 , y 1 ).
 Здесь координаты даны как (2, 4), (1, 2).
Здесь координаты даны как (2, 4), (1, 2). - Шаг 2: Примените формулу наклона линии, m = (y 2 — y 1 )/(x 2 — x 1 ) = (4 — 2)/(2 — 1) = 2,
- Шаг 3: Следовательно, наклон данной линии = 2.
Типы уклонов
Мы можем классифицировать наклон по различным типам в зависимости от отношения между двумя переменными x и y и, таким образом, от значения градиента или наклона полученной линии. Существует 4 различных типа уклонов, обозначенных как
- Положительный уклон
- Отрицательный наклон
- Нулевой наклон
- Неопределенный уклон
Положительный наклон
Графически положительный наклон указывает на то, что при движении слева направо в координатной плоскости линия поднимается, что также означает, что при увеличении x увеличивается и y.
Отрицательный наклон
Графически отрицательный наклон указывает на то, что при движении слева направо в координатной плоскости линия падает, что также означает, что при увеличении x уменьшается y.
Нулевой наклон
Для линии с нулевым наклоном подъем равен нулю, и, таким образом, применяя формулу превышения подъема, мы получаем нулевой наклон линии.
Неопределенный уклон
Для линии с неопределенным уклоном значение длины равно нулю. Наклон вертикальной линии не определен.
Наклон горизонтальной линии
Мы знаем, что горизонтальная линия — это прямая линия, параллельная оси x или проведенная слева направо или справа налево в координатной плоскости. Следовательно, чистое изменение координаты y горизонтальной линии равно нулю. Наклон горизонтальной линии можно определить как
Наклон горизонтальной линии, m = Δy/Δx = ноль
Наклон вертикальной линии
Мы знаем, что вертикальная линия — это прямая линия, параллельная оси Y или рисуется сверху вниз или снизу вверх в координатной плоскости. Следовательно, чистое изменение координат x вертикальной линии равно нулю. Наклон вертикальной линии можно определить как
Наклон вертикальной линии, м = Δy/Δx = не определено
Наклон перпендикулярных линий
Набор перпендикулярных линий всегда имеет между собой угол 90º. Предположим, что у нас есть две перпендикулярные линии l 1 и l 2 в координатной плоскости, наклоненные под углами θ 1 и θ 2 соответственно с осью x, так что данные углы следуют внешнему углу теорема как, θ 2 = θ 1 + 90º.
Предположим, что у нас есть две перпендикулярные линии l 1 и l 2 в координатной плоскости, наклоненные под углами θ 1 и θ 2 соответственно с осью x, так что данные углы следуют внешнему углу теорема как, θ 2 = θ 1 + 90º.
Следовательно, их наклоны можно представить как
м 1 = тангенс θ 1
м 2 = загар (θ 1 + 90º) = — раскладушка θ 1
⇒ m 1 × m 2 = -1
Таким образом, произведение наклонов двух перпендикулярных прямых равно -1.
Наклон параллельных линий
Набор параллельных линий всегда имеет одинаковый угол наклона. Предположим, у нас есть две параллельные линии l 1 и l 2 в координатной плоскости, наклоненные под углом θ 1 и θ 2 соответственно с осью x, так что θ 2 = θ 1 .
Следовательно, их наклоны могут быть указаны как
⇒ m 1 = m 2
Таким образом, наклоны двух параллельных прямых равны.
Важные примечания по наклону:
- Наклон линии — это мера тангенса угла, образуемого линией с осью x.
- Наклон постоянен на протяжении всей прямой.
- Форма пересечения наклона прямой линии может быть задана как y = mx + b
- Наклон обозначается буквой m и определяется выражением m = tan θ = (y 2 — y 1 )/(x 2 — x 1 )
Сложный вопрос:
Прямая имеет уравнение y = 2x — 7. Найдите уравнение прямой, перпендикулярной данной прямой и проходящей через начало координат.
☛ Похожие темы:
- Линейное уравнение
- Квадратное уравнение
- Кубическое уравнение
Часто задаваемые вопросы о склоне
Что такое наклон линии?
Наклон линии, также известный как градиент, определяется как значение крутизны или направление линии в координатной плоскости.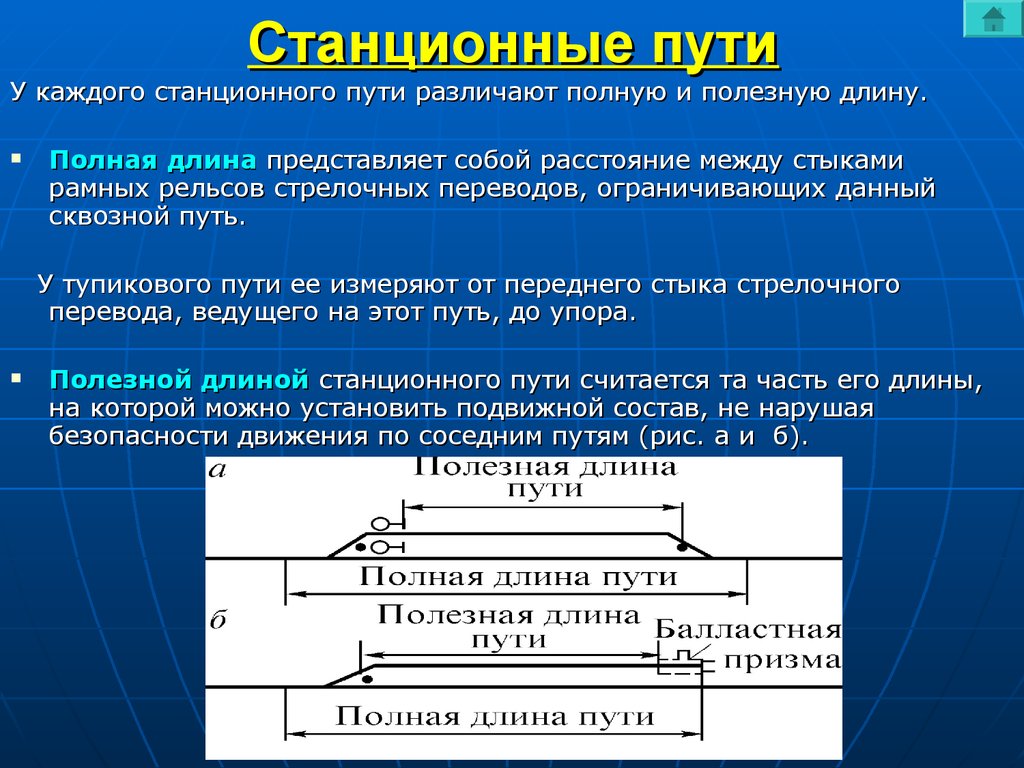 Уклон можно вычислить разными способами, зная уравнение прямой или координаты точек, лежащих на прямой.
Уклон можно вычислить разными способами, зная уравнение прямой или координаты точек, лежащих на прямой.
По какой формуле можно найти наклон линии?
Мы можем рассчитать наклон линии напрямую, используя формулу наклона линии, зная координаты двух точек, лежащих на линии. Формула дается как,
Уклон = m = tan θ = (y 2 — y 1 )/(x 2 — x 1 )
Как рассчитать уклон?
Наклон определяется путем измерения тангенса угла, образованного линией с осью x. Существуют различные методы определения наклона линии. Выражение, которое можно использовать для определения наклона, имеет вид tan θ или (y 2 — y 1 )/(x 2 — x 1 ), где θ — угол, который линия образует с положительной осью x, и (x 1 , y 1 ) и (x 2 , y 2 ) — координаты двух точек, лежащих на прямой.
Какие существуют 4 типа склонов?
Существует 4 различных типа наклона: положительный наклон, отрицательный наклон, нулевой наклон и неопределенный наклон.
Что такое неопределенный уклон?
Любой уклон с углом 90º с осью x, будет иметь неопределенное значение тангенса 90º. Следовательно, такие линии будут иметь неопределенное значение наклона.
Как выглядит склон?
Наклон — это не что иное, как мера тангенса угла, составленного с осью x. Следовательно, это всего лишь мера угла.
Какие 3 способа найти уклон?
Способы определения уклона: форма точечного уклона, форма пересечения уклона и стандартная форма. Мы можем применить любую из форм уравнения прямой линии, учитывая необходимую информацию, чтобы найти наклон.
Как показать, что три точки лежат на одной прямой по наклону?
Чтобы доказать коллинеарность трех точек, скажем, A, B и C, мы можем применить формулу наклона. Наклон прямых AB и BC должен быть одинаковым, чтобы три заданные точки были точками на одной прямой.
Как найти уклон по двум точкам?
Наклон можно рассчитать, используя координаты двух точек по формуле m = (y 2 — y 1 )/(x 2 — x 1 ), где (x 1 , y 1 ) и (x 2 , y 2 ) — координаты двух точек, лежащих на прямой.
Наклон линии – объяснение и примеры
Наклон линии определяется как t he c изменение значений y, деленное на изменение значений x. Это число показывает, насколько крута линия.
Наклон линии не определяет ее однозначно, но дает нам много информации. Это также необходимый компонент уравнения линии.
Наклон линии часто представляет собой дробь, поэтому перед чтением этого раздела рекомендуется просмотреть дроби. Также может помочь обзор координатной геометрии и координатной плоскости.
В этом разделе рассматриваются следующие темы:
- Что такое наклон линии?
- Как вычислить наклон линии
- Как найти наклон по двум точкам
Что такое наклон линии?
Наклон линии — это число, используемое для описания того, насколько крута линия. Это число может быть положительным, отрицательным или нулевым. Он также может быть рациональным или иррациональным.
Он также может быть рациональным или иррациональным.
Наклон линии не определяет ее однозначно. Это означает, что если вы знаете наклон линии, вы не можете точно сказать, через какие точки она проходит.
Параллельные линии — это любые линии с одинаковым наклоном. Перпендикулярные прямые — это прямые, которые становятся параллельными при повороте на 90 градусов. Если две перпендикулярные линии пересекутся, они образуют четыре угла по 90 градусов.
Линия с наклоном 0 является горизонтальной линией. Любая линия, которая движется вверх по мере того, как она идет дальше вправо, является положительной. И наоборот, любая линия, которая движется вниз по мере того, как она идет дальше влево, является отрицательной.
Говорят, что вертикальная линия, такая как ось Y, имеет «неопределенный» наклон. Это связано с тем, как математически определяется уклон, который мы обсудим более подробно ниже.
Как рассчитать уклон линии
Уклон обычно обозначается буквой m. Интересно, что нет единого мнения о том, почему именно эта буква была выбрана. Однако любой, кто знает французский, может легко запомнить это, потому что слово «монтер» означает «карабкаться». Это слово имеет то же происхождение, что и английское слово «гора», которое также может служить мнемоникой, поскольку у гор есть склоны.
Интересно, что нет единого мнения о том, почему именно эта буква была выбрана. Однако любой, кто знает французский, может легко запомнить это, потому что слово «монтер» означает «карабкаться». Это слово имеет то же происхождение, что и английское слово «гора», которое также может служить мнемоникой, поскольку у гор есть склоны.
Находим наклон, разделив изменение значений y на изменение значений x. Неважно, какие координаты мы выберем для этого расчета, потому что отношение остается постоянным.
Как найти уклон по двум точкам
Самый простой способ найти уклон — найти две пары координат для точек на линии. Назовите эти две точки (x 1 , y 1 ) и (x 2 , y 2 ). Обратите внимание, что не имеет значения, какая точка помечена как какая.
Формула для уклона: m = (y 1 -y 2 ) ⁄ (x1-x2) .
Помните, что уклон — это «подъем над прогоном», чтобы случайно не поменять местами значения x и y в формуле.
Если линия проходит через точки (1, 2) и (-1, -1), обозначьте первую точку (x 1 , y 1 ) и вторую (x 2 , y 2 ). Тогда его наклон равен:
м = (2+1) ⁄ (1+1) = 3 ⁄ 2 .
Это означает, что на каждые две единицы линия смещается вправо, она будет двигаться вверх на три единицы.
Мы также можем посмотреть на координатную плоскость с двумя точками и найти наклон графически, используя две точки. Рассмотрим, например, координатную плоскость ниже.
Сначала нужно найти две точки, лежащие на прямой. Имеет смысл использовать самые простые возможные точки, поэтому начало координат и точка (1, 2) имеют наибольший смысл.
Чтобы перейти от первой точки ко второй, нам нужно переместиться «на две (единицы) вверх, на одну (единицу вправо)». Произнесение этого вслух во время подсчета единиц дает наклон. В данном случае действительно 2 ⁄ 1 или «два больше одного».
Мы можем перепроверить это, подставив значения в приведенную выше формулу. Если (0, 0) равно (x 1 , y 1 ), а (1, 2) равно (x 2 , y 2 ), мы имеем:
m = (0-2 ) ⁄ (0-1) = -2 ⁄ -1 =2.
Обратите внимание, что графический подсчет для определения наклона работает только тогда, когда набор данных включает рациональные числа, которые легко идентифицировать с помощью масштаба графика.
Отрицательный наклон
Оба приведенных выше примера имеют положительный наклон. Однако поиск отрицательного наклона очень похож.
Рассмотрим, например, две точки (10, 0) и (0, 50), лежащие на прямой. Затем мы помечаем их (x 1 , y 1 ) и (x 2 , y 2 ) соответственно. Используя эту информацию, наклон линии составляет:
м = (0-50) ⁄ (10-0) = -50 ⁄ 10 = -5.
Обратите внимание, что порядок, в котором мы выбираем точки, не имеет значения.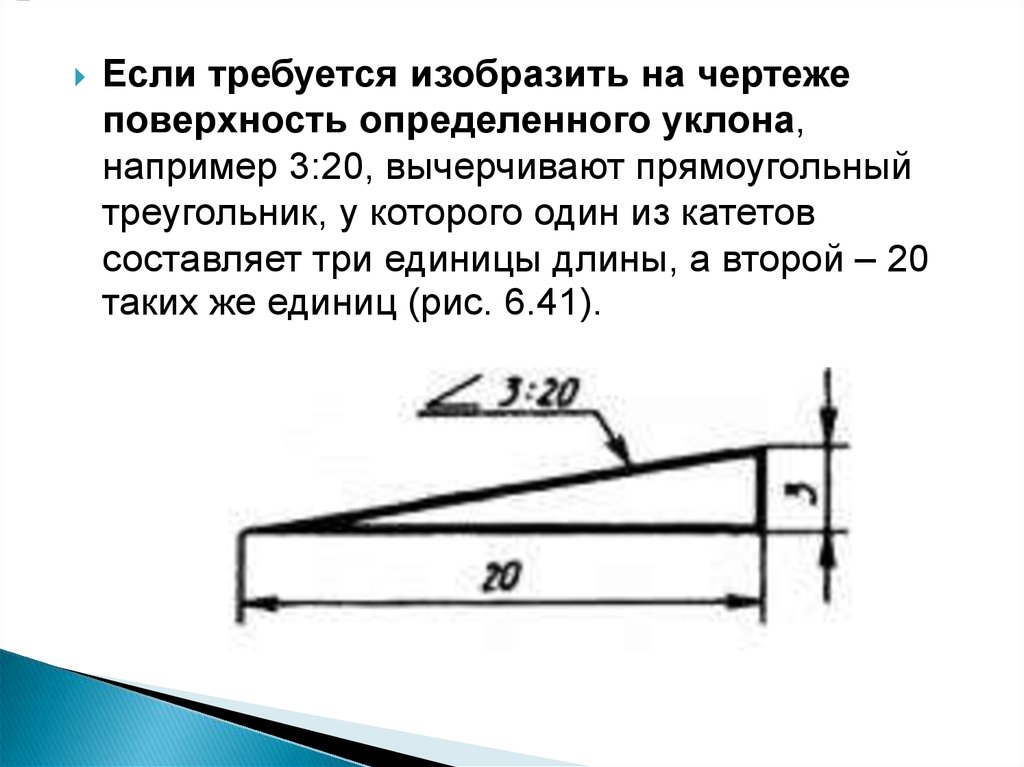 Если бы мы выбрали (10, 0) равным (x 2 , y 2 ) и (0, 50) равно (x 1 , y 1 ), наше уравнение будет таким: -10) = 50 ⁄ -10 = -5.
Если бы мы выбрали (10, 0) равным (x 2 , y 2 ) и (0, 50) равно (x 1 , y 1 ), наше уравнение будет таким: -10) = 50 ⁄ -10 = -5.
Графический поиск отрицательных наклонов работает так же, как и поиск положительных наклонов в графическом виде. Рассмотрим линию, показанную ниже:
Эта линия проходит через точки (0, 3) и (3, 2). Чтобы добраться из одной точки в другую, нам нужно спуститься «на одну (единицу) вниз, на три (единицы вправо)». Поскольку «вниз» означает отрицательное движение, наклон линии равен -1 ⁄ 3 , «минус один больше трех».
Опять же, это означает, что на каждые три единицы эта линия смещается вправо или на одну единицу вниз.
Нулевой наклон и неопределенный наклон
Что происходит, когда наша линия строго горизонтальна или строго вертикальна?
Обратите внимание на красную горизонтальную и синюю вертикальную линии на изображении ниже.
Найдем наклон каждого из них.
Красная линия проходит через точки (0, 2) и (1, 2). Это означает, что его наклон:
м = (2-2) ⁄ (0-1) = 0 ⁄ -1 =0.
Эта горизонтальная линия, как и все горизонтальные линии, имеет наклон 0, поскольку ее высота никогда не меняется.
Синяя линия, напротив, проходит через точки (2, 0) и (2, 1). Это означает, что его наклон равен:
м = (0-1) ⁄ (2-2) = -1 ⁄ 0 …
и это проблема, потому что мы не можем делить на ноль. Следовательно, эта вертикальная линия, да и все вертикальные линии, имеют неопределенный наклон. Это имеет смысл, потому что его высота — это все высоты одновременно.
Другие способы определения уклона
Использование заданных координат (или нахождение координат), а затем их подстановка в уравнение уклона — самый прямой способ определения уклона. Однако это не единственный способ сделать это.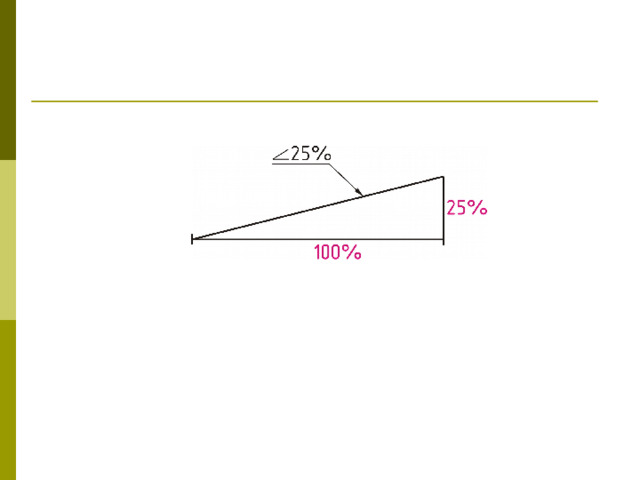 Иногда информация о других линиях является лучшим методом.
Иногда информация о других линиях является лучшим методом.
Параллельные прямые
Параллельные прямые имеют одинаковый наклон, и существует бесконечно много прямых, параллельных данной прямой. Каждая линия будет просто пересекать оси x и y в разных точках.
Например, две линии, показанные ниже, параллельны.
Красная линия пересекает обе оси в начале координат. Однако синяя линия пересекает ось Y в точке (0, 1). Затем он пересекает ось x в точке (-4, 0). Однако, поскольку их наклоны одинаковы, они параллельны.
Если мы знаем наклон одной прямой и знаем, что другая прямая параллельна, мы можем легко определить наклон второй прямой.
Например, на изображении выше наклон красной линии легче найти, поскольку она проходит через начало координат. Если (0, 0) равно (x 1 , y 1 ), а (4, 1) равно (x 2 , y 2 ), наклон: ) = -1 ⁄ -4 = 1 ⁄ 4 .
Поскольку синяя линия параллельна, формулу можно обойти. Его наклон также равен 1 ⁄ 4 .
Перпендикулярные линии
Перпендикулярные линии пересекаются под углом 90 градусов. Подобно параллельным прямым, существует бесконечно много прямых, перпендикулярных данной прямой. Они просто встретятся с заданной линией в разных точках.
Наклоны двух перпендикулярных линий связаны. Каждый является противоположным знаком, обратным другому.
Напомним, что обратная дробь — это обратная дробь. Чтобы найти его, просто переверните дробь вверх ногами.
Если наклон представляет собой целое число, например -8, или десятичное число, например 0,8, сначала преобразуйте число в дробь. -8 становится -8 ⁄ 1 и 0,8 становится 8 ⁄ 10 или 4 ⁄ 5 .
Затем переверните дробь вверх ногами и поменяйте знак. -8 ⁄ 1 становится 1 ⁄ 8 и 4 ⁄ 5 становится -5 ⁄ 0 4 90. Это означает, что линия с наклоном 1 ⁄ 8 перпендикулярна линии с наклоном 8, а линия с наклоном -5 ⁄ 4 перпендикулярна линии с наклоном 4 ⁄ 5 .
Это означает, что линия с наклоном 1 ⁄ 8 перпендикулярна линии с наклоном 8, а линия с наклоном -5 ⁄ 4 перпендикулярна линии с наклоном 4 ⁄ 5 .
Знание того, что линии перпендикулярны, может, следовательно, помочь нам быстрее найти уклон.
Например, на изображении ниже красная и синяя линии перпендикулярны.
Опять же, поскольку красная линия пересекает начало координат, ее наклон легче определить. Пусть (0, 0) будет (x 1 , y 1 ), а (3, 2) будет (x 2 , y 2 ). Тогда
м = (0-2) ⁄ (0-3) = -2 ⁄- 3 = 2 ⁄ 3 .
Наклон синей линии обратно пропорционален. 2 ⁄ 3 инвертировано 3 ⁄ 2 , а добавление отрицательного знака дает -3 ⁄2. Следовательно, -3 ⁄2 — это наклон синей линии.
Значение в реальном мире
Уклон также имеет значение в реальном мире. Вспомните, что мы часто называем ось X «независимой переменной», а ось Y — «зависимой переменной». Это означает, что изменение переменной x вызывает изменение переменной y.
Вспомните, что мы часто называем ось X «независимой переменной», а ось Y — «зависимой переменной». Это означает, что изменение переменной x вызывает изменение переменной y.
На самом деле мы все время используем наклон, даже не осознавая этого. Когда мы говорим о скорости, например, «миль в час», когда говорим о скорости автомобиля, или «дюймы в год», когда говорим о росте растения, мы говорим об уклоне.
Например, если мы отложим время по оси x и мили, пройденные какой-либо машиной по оси y, наклон линии будет равен количеству миль, пройденных этой машиной за час. Если автомобиль стартовал со скоростью 0 миль за 0 часов и проехал 50 миль за один час, его скорость составит (0-50) ⁄(0-1)= -50 ⁄-1=50 миль в час. Это также наклон линии, соединяющей две точки!
Следовательно, наклон можно рассматривать как коэффициент.
Примеры
В этом разделе будут рассмотрены примеры распространенных типов задач, связанных с наклоном линии. Он также будет включать в себя пошаговые решения к ним.
Он также будет включать в себя пошаговые решения к ним.
Пример 1
Зная, что точки (8, 7) и (-20, 14) лежат на прямой, найдите наклон прямой.
Пример 1 Решение
Поскольку нам даны две точки, мы можем использовать уравнение для наклона линии. Пусть (8, 7) будет (x 1 , y 1 ) и (-20, 14) будет (x 2 , y 2 ). Затем, подставляя значения в формулу, мы получаем:
м = (7-14) ⁄ (8+20) = -7 ⁄ 28 = -1 ⁄ 4 .
Таким образом, наклон линии равен -1 ⁄ 4 .
Примечание. Можно определить уникальное уравнение линии по двум точкам, но этот процесс выходит за рамки данного урока.
Пример 2
Найдите наклон красной линии, показанной на графике ниже.
Пример 2 Решение
Мы можем использовать график, чтобы найти две точки, чтобы включить их в нашу формулу наклона.
Так как точки (1, 2) и (3, -7) лежат на прямой, будем использовать их. Пусть (1, 2) будет (x 1 , y 1 ), а (3, -7) будет (x 2 , y 2 ). Тогда имеем:
Пусть (1, 2) будет (x 1 , y 1 ), а (3, -7) будет (x 2 , y 2 ). Тогда имеем:
м = (2+7) ⁄ (1-3) = 9 ⁄ -2 = -9 ⁄ 2 .
Следовательно, наклон равен -9 ⁄ 2 .
Эту задачу можно было решить и графически. Чтобы добраться из первой точки во вторую, нам нужно спуститься «вниз на 9(единицы), более 2 (единицы справа)». Поскольку «вниз» указывает отрицательное направление, наклон составляет 90 552 -9 90 557 ⁄ 90 089 2 90 090, читается как «минус 9 на 2».
Пример 3
Наклон линии p равен 3 ⁄ 5 . Если точки (8, -9) и (2x, -3) лежат на прямой, каково значение x?
Пример 3 Решение
Мы снова можем использовать формулу для наклона, но нам нужно действовать в обратном порядке. Пусть (8, -9) будет (x 1 , y 1 ), и пусть (2x, -3) будет (x 2 , у 2 ). Помните, что мы уже знаем m= 3 ⁄ 5 . Таким образом, мы имеем
Помните, что мы уже знаем m= 3 ⁄ 5 . Таким образом, мы имеем
3 ⁄ 5 = (-9+3) ⁄ (8-2x)
3 ⁄ 5 = -6 ⁄ 5 = -6 ~ 5 = -6 Сое. -х)) .
Умножение обеих частей на 2(4-x) дает нам:
3 ⁄ 5 ×2(4-x)=-6
6 ⁄ 5 6
24 ⁄ 5 – 6x ⁄ 5 = -6.
Затем, вычитая 24 ⁄ 5 с обеих сторон ⁄ 5 =- 54 ⁄ 5
Наконец, умножение обеих сторон на -5 ⁄ 6 дает нам:
x = (-54 × -5)
9 (-54 × -5)
(
x = (-54 × -5)
(
9
(-54 × -5) 6)
х=9.
Следовательно, поскольку x=9, точка (2x, -3) на самом деле равна (2×9, -3)=(18, -3).
Пример 4
Найдите наклон любой прямой, перпендикулярной прямой, проходящей через точки (-1, 5) и (-7, 7).
Пример 4 Решение
Сначала мы должны найти наклон данной линии. Затем мы можем вычислить обратную величину этого наклона, чтобы определить наклон линии, перпендикулярной данной линии.
Пусть (-1, 5) будет (x 1 , y 1 ), и пусть (-7, 7) будет (x 2 , у 2 ). Тогда мы можем вычислить уклон как:
м = (5-7) ⁄ (-1+7) = -2 ⁄ 6 =- 1 ⁄
Так как наклон равен – 1 ⁄ 3 , обратное значение равно +3, или всего 3. Следовательно, любая линия, перпендикулярная данной прямой, будет иметь наклон 3.
Пример 5
Линия k проходит через точки (2, 3) и (-1, 8). Линия l показана ниже.
Прямые k и l параллельны, перпендикулярны или ни те, ни другие?
Пример 5 Решение
В этом случае нам нужно будет найти наклоны обеих линий и сравнить их.
Сначала рассмотрим линию k. Пусть (2, 3) будет (x 1 , y 1 ), а (-1, 8) будет (x 2 , y 2 ).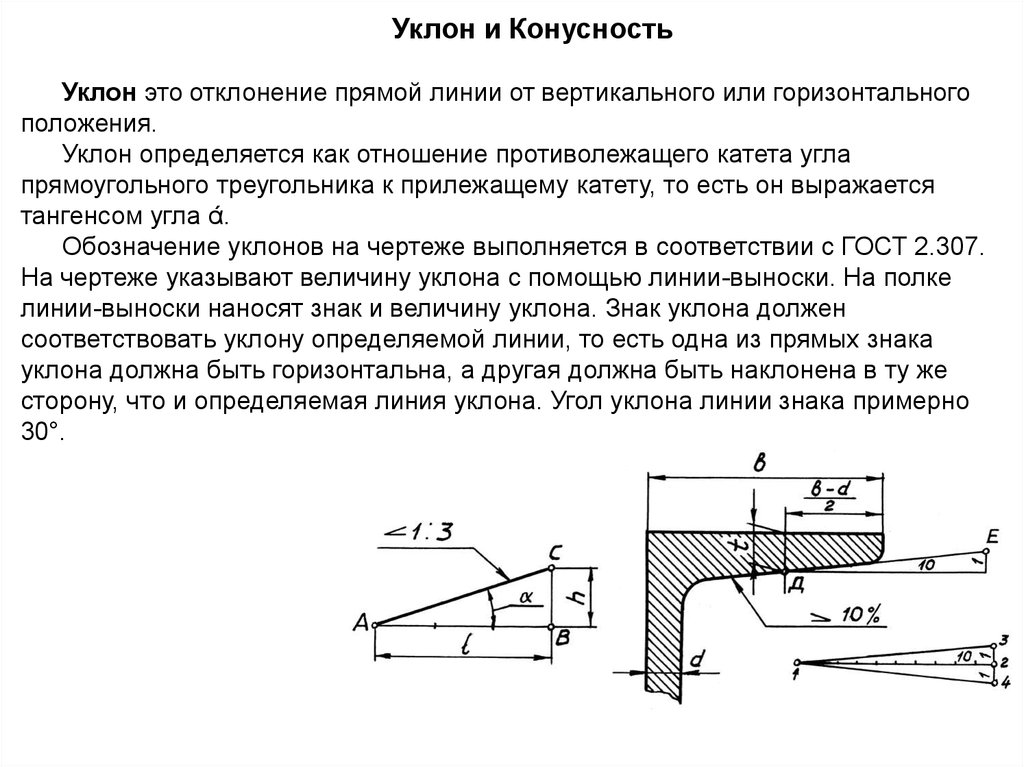 Тогда имеем:
Тогда имеем:
м = (3-8) ⁄ (2+1) = 5 ⁄ 3 .
Следовательно, наклон k равен 5 ⁄ 3 .
Далее рассмотрим линию l. Ясно, что он проходит через точки (0, 0) и (5, -3). Если начало координат (x 1 , y 1 ) и (5, -3) равно (x 2 , y 2 ), мы имеем:
m = (3-0) ⁄ (5-0) = -3 ⁄ 5 .
Следовательно, наклон l равен -3 ⁄ 5 .
Любая линия, параллельная k, имеет наклон 5 ⁄ 3 , поэтому l не параллельна.
Любая линия, перпендикулярная k, будет иметь наклон, противоположный обратному значению k, который равен -3 ⁄ 5 . Так как l имеет наклон -3 ⁄ 5 , две прямые перпендикулярны.
Пример 6
Подводная лодка на глубине 33 фута ниже уровня моря испытывает давление воды над ней приблизительно 14,7 фунтов на квадратный дюйм. Другая подводная лодка на глубине 66 футов ниже уровня моря испытывает примерно 29,4 фунта на квадратный дюйм давления воды над ней. Нанесите эти точки на график и проведите линию, соединяющую их. Каков наклон этой линии и каково ее реальное значение?
Другая подводная лодка на глубине 66 футов ниже уровня моря испытывает примерно 29,4 фунта на квадратный дюйм давления воды над ней. Нанесите эти точки на график и проведите линию, соединяющую их. Каков наклон этой линии и каково ее реальное значение?
Пример 6 Решение
Сначала нам нужно определить, является ли давление или глубина независимой переменной. Поскольку давление зависит от глубины, а не наоборот, глубина является независимой переменной, а давление — зависимой переменной. Это означает, что переменная x — это глубина, а переменная y — давление.
Следовательно, наши точки (33, 14.7) и (66, 29.4). Координатная плоскость ниже включает две точки и линию, проходящую через них.
Пусть (33, 14.7) будет (x 1 , у 1 ) и (66, 29.4) быть (х 2 , у 2 ). Тогда уклон равен:
м = (29,4-14,7) ⁄ (66-33) = 14,7 ⁄ 33 .
Таким образом, наклон равен 14,7 ⁄ 33 , что в единицах измерения можно прочитать как «14,7 фунтов на квадратный дюйм на 33 фута».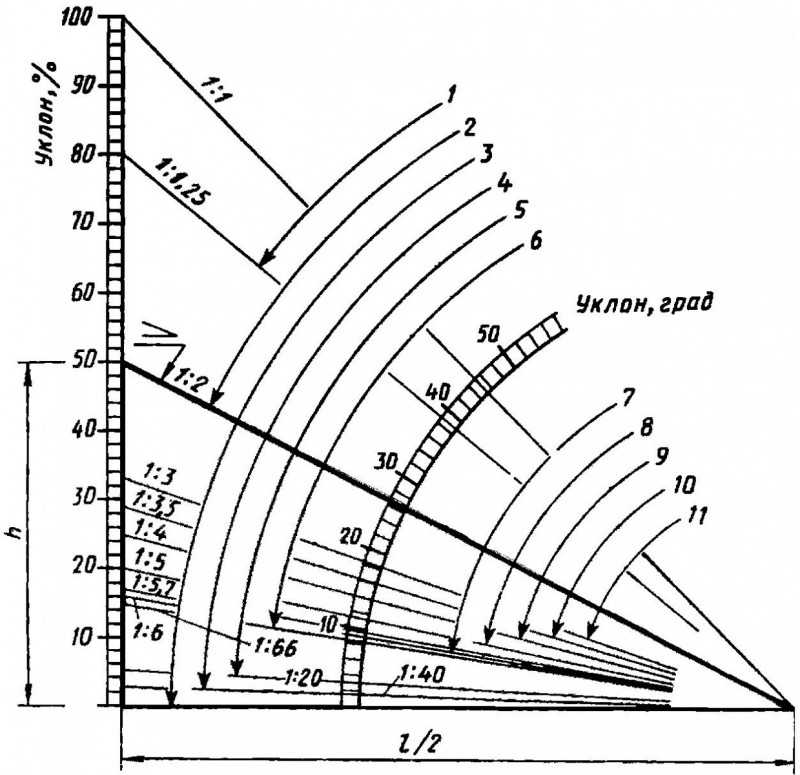
 Здесь координаты даны как (2, 4), (1, 2).
Здесь координаты даны как (2, 4), (1, 2).