Что такое сечение в геометрии: Построение сечений

Математика — Геометрия — Стереометрия

• Главная

  —

• Формулы и прочее

  —

• Математика: Построение сечений

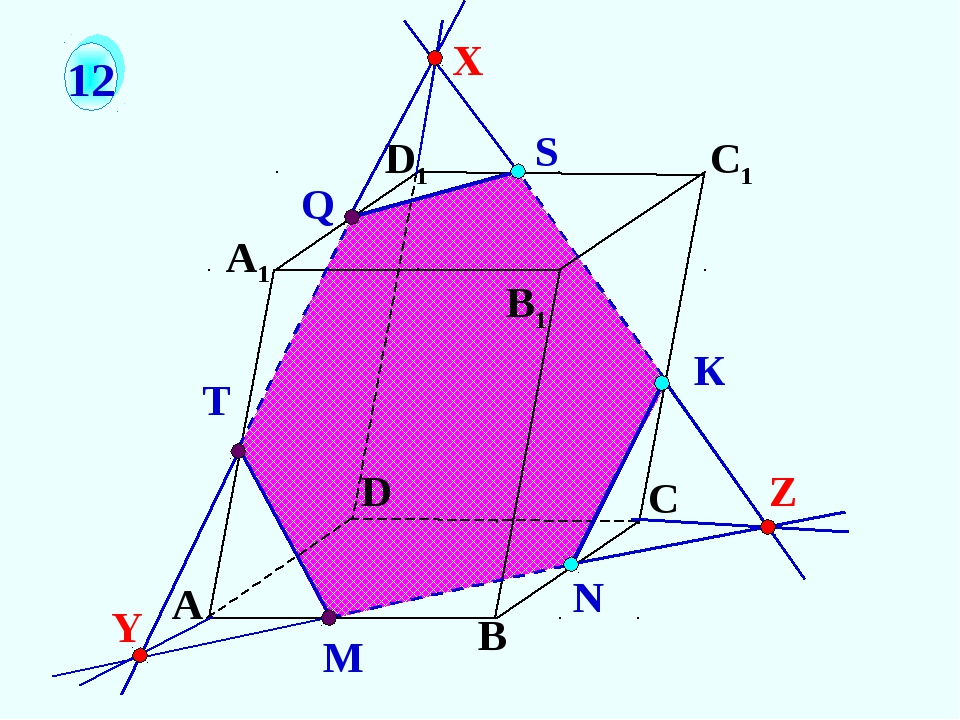
Построение сечений объемных фигур при решении геометрических задач по стереометрии часто вызывает у абитуриентов определенные сложности. При этом на ЦТ и ЕГЭ по математике иногда приходится выполнять такую процедуру. Далее представлен алгоритм построения простейших сечений пространственных фигур и объемных тел.

Алгоритм построения простейших сечений:

1. Соединяем точки сечения, лежащие на одной грани прямыми. При этом участки получающихся прямых, заключенные между ребрами, становятся отрезками сечения. Повторяем этот процесс до тех пор, пока не исчерпаем все подобные возможности, и только потом переходим ко второму пункту.
2. Продлеваем какой-нибудь отрезок сечения и какое-либо ребро, лежащее с ним в одной грани до пересечения.
3. Смотрим, какой грани принадлежит точка пересечения. Если в этой грани есть точки сечения, то соединяем полученную ранее точку пересечения и имеющуюся точку сечения прямой. При этом участки получающихся прямых, заключенные между ребрами (но не их продолжениями), становятся отрезками сечения.
4. Затем повторяем процесс (начиная с первого пункта), пока сечение не замкнется.

ЗАМЕЧАНИЕ: Пересекаются только прямые, лежащие в одной плоскости (осознание этого факта для правильного построения сечений важнее знания самого алгоритма построения этих самых сечений).

ЗАМЕЧАНИЕ: Приведенный алгоритм не универсальный. Вы должны быть готовы к тому, что он не сработает, а Вам придется проявить смекалку. Универсального алгоритма построения сечений многогранников, к сожалению, не существует.

• Назад

• Вперёд

Как успешно подготовиться к ЦТ по физике и математике?

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

1. Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
2. Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
3. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

Сечение многогранников: параллелепипеда и тетраэдра (урок геометрии)

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1
В1
M
N
С1
Д
Д1
А1
K
Q
R
В
С
F
А
В
P
А
L
Д
С
2
Секущей плоскостью, называют любую плоскость, по обе стороны
от которой имеются точки данного многогранника. Секущая
плоскость пересекает грани многогранника по отрезкам.
Многоугольник, сторонами которого являются эти отрезки,
называется сечением многогранника.
Сечением параллелепипеда может быть:
треугольник
пятиугольник
D1
С1
В1
А1
А1
А1
В
В
С
А
D
D1
D1
В
С
В
D
С
четырехугольник
А
А1
С1
В1
D1
С1
В1
С1
В1
А
D
А
С
D
шестиугольник
3

4.

Сечением тетраэдра может быть:

треугольник
четырехугольник
D
М
D
N
А
M
С
N
А
С
K
P
В
В
4

5. Теория, необходимая при построении сечений

• Если две точки прямой лежат в плоскости, то все точки прямой
лежат в этой плоскости
В
α
А
A
є α
B
є α
AB є α
5

6. Теория, необходимая при построении сечений

• Через любую точку пространства, не лежащую на
данной прямой, проходит прямая, параллельная
данной, и притом только одна
b
М
◦
а
β
6

7. Теория, необходимая при построении сечений

• Если две параллельные плоскости пересечены
третьей, то линии их пересечения параллельны
γ
α
ββ
a
b
α
║ β
α
γ ∩
= a
γ ∩
a ║ b
β = b
7

8. При построении сечений часто используется метод следа, необходимость в котором возникает в том случае, если в плоскости грани многогранни

При построении сечений часто используется метод
следа, необходимость в котором возникает в том
случае, если в плоскости грани многогранника лежит
всего одна точка плоскости сечения
N С1
В1
М
А1
D1
F
є (А1В1С1)
P
К є (DCC1)
(А1В1С1) ∩ (DCC1) =
М, N
∩ D1C1 =
K, F є (DCC1)
МN
В
KF∩ CC1 = P
F
С
К
А
D1C1
D
Используя метод следа найдите вторую
точку плоскости сечения и грани АDD1
8
В1
E А1
N
С1
F
М
M, N є (A1B1C1)
D1
P
L
В
К
С
K є (ADD1)
(A1B1C1)
∩ (ADD1) = A1D1
A1D1
= E
MN ∩
K,E є (ADD1)
KE ∩
А
D
AA1
=
L
(α-плоскость сечения)
N С1
В1
М
А1
F
P
D1
α ∩ (CDD1) = KP
α ∩ (ABB1) = ML
L
В
С
К
А
(CDD1) ║ (ABB1)
D
KP ║ ML
Построить сечение параллелепипеда плоскостью, проходящей через
точки М, N, К.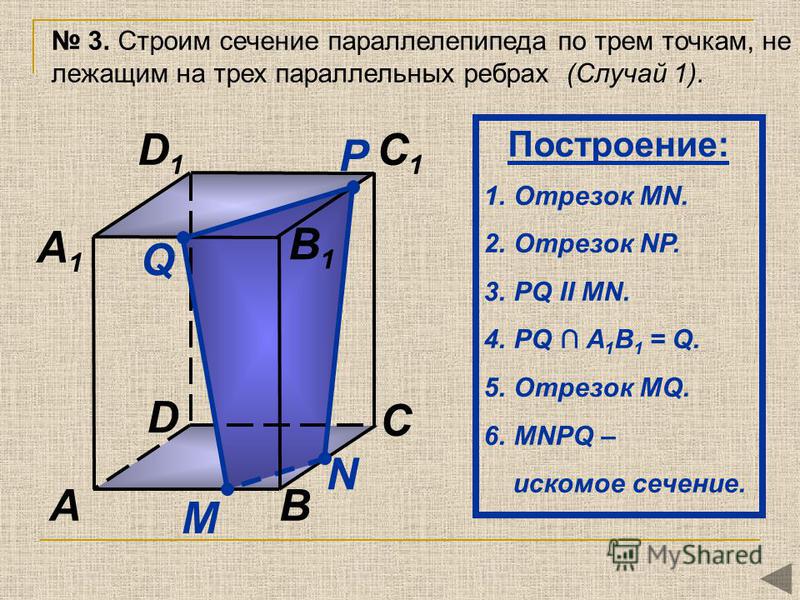
1) М, N
В1
С1
L
E D1
А1
К
F
В
М
А
D
(ВСС1)
М, N є α
(ADD1) (ВСС1)
║
(ВСС1)
∩ α = MN
(ADD)
∩ α = KE
(ADD1)
N 3) КЕ є
(ABC )
є
M
2)
С
P
є
(ВСС1)
KE
∩ α=
МN
║ MN
Используя метод следа, найдите
вторую точку сечения,
принадлежащую плоскости АВС
Достройте сечение
є
11
Построить сечение тетраэдра плоскостью α , проходящей через
точки М, N, К.
1)
D
M
2)
N
А
В
K
С
(ABD)
є
M, N
(ABD)
M, N
є
M,K
є
(АСD)
M,K
є
α
3) K,N
K,N
є
є
α
(АСD)
∩ α = MN
∩ α = MK
(BCD)
(BCD)
α
∩ α = KN
4) (MNK) – плоскость сечения α
12
Построить сечение тетраэдра плоскостью α , проходящей через точки
М, N, К.
1)
D
є
є
М
N
2) М
K
M
є
є
(ABD)
( АСD)
( АСD)
K
(ABD)
MK
є
( АСD)
3) М, N є (ABD)
K є (ABC)
(ABD) ∩ (ABC) = AB
МN ∩ AB = L
R
С
K, L
N
є
L
В
R
MN
N
А
4)
(ABD)
є
є
(BCD)
(BCD)
RN
є
(BCD)
5)
є
KL ∩ BC = R
(ABC)
(MNRK) – искомая плоскость α
13

English    
Русский
Правила

dg.

дифференциальная геометрия — Что такое сечение?

На ваш первый вопрос «функция на пространстве» $X$ обычно означает морфизм из $X$ в одно из нескольких «наземных пространств» по выбору, например, вещественные числа, если вы работаете с гладкими многообразиями, Spec( А) если вы работаете со схемами над кольцом и т. д. (это довольно избирательное употребление слова «функция», которое раньше меня смущало.) Сечение $\gamma$ (какого-то) пучка $ E\to X$ рассматривается как «обобщенная функция» на $X$, если думать о ней как о функции с «переменной кодовой областью», т.е. в каждой точке $x\in X$ она принимает значение в слое
$E_x\до x$. Если речь идет о локально свободных/локально тривиальных расслоениях, то есть $E$ локально (над открытыми множествами
$U\subset X$) изоморфна некоторому произведению $U\times T$, то мы можем локально отождествлять слои с $ Т$. Таким образом, локально секция просто выглядит как функция с кодовым доменом $T$, что часто требуется, чтобы быть хорошим.

На ваш второй вопрос: Обычно я беру определение «право-обратное» или «предобратное» из теории категорий, потому что оно соотносится с другими точно следующим образом:

Скажем, $\pi: Y\to X$ — пространство над $X$ (намеренно расплывчатое). Слово «над» используется, чтобы активировать традицию подавления ссылки на карту $\pi$ и ссылки вместо нее на домен $Y$. Для открытого $U\subseteq X$ обозначение $\Gamma(U,Y)$ обозначает сечений отображения $\pi$ над $U$ , т.е. отображает $U\в Y$ такие, что композиция $U \to Y\to X$ является тождеством (таким образом, обязательно возвращаясь обратно в $U$). Нетрудно заметить, что
$\Gamma(-,Y)$ на самом деле образуют пучок множеств на $X$.

Наоборот, для любого пучка множеств $F$ в пространстве $X$ можно составить его espace etalé, топологическое пространство над $X$, скажем, $\pi: \acute{E}t(F) \to Х$. Тогда для открытого $U\subseteq X$ элементы $F(U)$ соответствуют в точности сечениям отображения $\pi$, которое в приведенных выше обозначениях записывается как $\Gamma(U,\acute{E} t(F)$, то есть
$F(-)\simeq\Gamma(-,\acute{E}t(F))$ как пучки на $X$. Это объясняет, почему люди часто называют пучок элементы как «секции» связки

Кроме того, то, что мы теперь обозначаем через $\acute{E}t(F)$, на самом деле раньше было определением пучка, поэтому люди склонны отождествлять их и писать $\Gamma(-,F)$ a вместо $\Gamma(-,\acute{E}t(F))$. Это объясняет причудливую традицию писать $\Gamma(U,F)$ вместо более компактного обозначения $F(U)$.

$\Big($ Неудачное лингвистическое предупреждение: Многие люди неправильно используют термин «пространство étale». Однако французское слово «étale» означает «распространенный», тогда как «étale» (без второго ударения) означает » спокойный », и они не предназначались для взаимозаменяемого использования в математике. Это прискорбно, потому что espace etalé имеет очень мало общего с этальными когомологиями. Еще более досадным является досадное совпадение, что при работе со схемами карта проекции из espace etalé оказывается этальным морфизмом, потому что локально в своей области определения он является изоморфизмом схем, что является гораздо более сильным условием. $\Big)$

На ваш третий вопрос: Я думаю, что наблюдение, что $\Gamma(-,Y)$ образует пучок на $X$, дает хороший контекст для размышлений о сечениях от $X$ до $Y$: они » жить в пучке $\Gamma(-,Y)$ как его глобально определенные элементы.

Поперечный разрез

Поперечный разрез

Поперечный разрез

В последовательность Plane Geometry узла Work Plane можно добавить узел Cross Section (). По умолчанию это вычисляет поперечное сечение всех 3D-объектов, созданных предыдущими узлами в последовательности геометрии. Вы также можете выбрать определенные 3D-объекты для пересечения с рабочей плоскостью. Вы также можете добавить новый 2D или 2D осесимметричный Компонент и добавить туда узел Поперечное сечение. В этом случае вы можете выбрать, какую рабочую плоскость использовать. Например, если у вас есть трехмерная геометрия, симметричная относительно оси, вы можете добавить рабочую плоскость, содержащую эту ось. Затем в осесимметричном 2D-компоненте вы получаете поперечное сечение и можете использовать 2D-осесимметричный компонент, который более эффективен в вычислительном отношении по сравнению с полным 3D-компонентом. Узел поперечного сечения также может быть полезен для извлечения плоской поверхности для моделирования тонкой плоской трехмерной структуры с использованием, например, элементов оболочки. Другое использование поперечного сечения — формирование поверхности, которую можно выдавить в 3D-тело из замкнутой кривой, лежащей в плоскости. Затем также добавьте узел «Преобразовать в твердое тело» под узлом «Поперечное сечение», чтобы превратить замкнутую кривую в 2D-поверхность.

Чтобы добавить поперечное сечение, щелкните правой кнопкой мыши узел плоской геометрии под узлом рабочей плоскости или узлом двумерной геометрии и выберите Поперечное сечение (). Затем введите свойства поперечного сечения, используя следующие сечения:

Поперечный разрез

Если вы добавляете узел «Поперечное сечение» в двухмерную или двухмерную осесимметричную геометрию, сначала выберите рабочую плоскость для поперечного сечения в списке «Рабочая плоскость».

В списке «Пересечение» выберите «Все объекты» (по умолчанию), чтобы пересечь все объекты 3D-геометрии с рабочей плоскостью, или выберите «Выбранные объекты», чтобы пересечь только те геометрические объекты, которые вы добавили в появившийся список «Объекты для пересечения». Нажмите кнопку «Активно», чтобы включить или выключить объекты для пересечения выбранных объектов.

Вы можете изменить настройки списка допусков для ремонта, если у вас возникли проблемы с операцией поперечного сечения. Геометрические объекты, расстояние между которыми меньше допуска на ремонт, объединяются.

При построении этого элемента относительные и абсолютные допуски на ремонт устанавливаются в соответствии с используемыми значениями (с точностью до двух цифр), что может быть полезно, если для параметра Допуск на ремонт установлено значение Автоматически.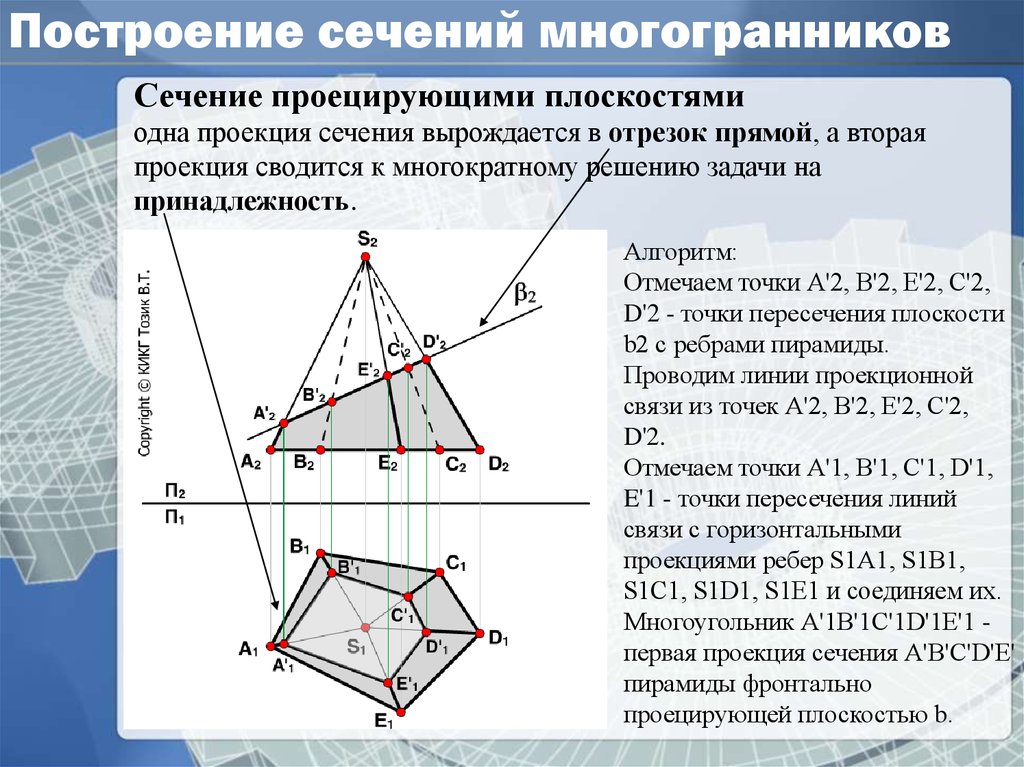

Выбор результирующих сущностей

Установите флажок Результирующий выбор объектов, чтобы создать предопределенные выборки (для всех применимых уровней — объектов, доменов, границ, ребер и точек) в последующих узлах последовательности геометрии. Используйте список «Показать в 3D» (для узлов поперечного сечения в геометрии плоскости узла «Рабочая плоскость») или список «Показать в физике» (или узлы поперечного сечения в 2D или 2D осесимметричных геометриях), чтобы выбрать, для какого уровня геометрического объекта должен быть создан выбор. Доступны все применимые уровни, а также Все уровни и Выкл. В списке Цвет выберите цвет для выделения результирующего выбора объектов. См. Цвета выделения.

Установите флажок Выборки из 3D, чтобы создать выборки в 2D на основе выборок из 3D-геометрии. Каждое выделение, созданное элементом 3D-геометрии, предшествующим рабочей плоскости в последовательности 3D-геометрии, и каждое кумулятивное 3D-выделение пересекаются с рабочей плоскостью, чтобы получить выделение в 2D.