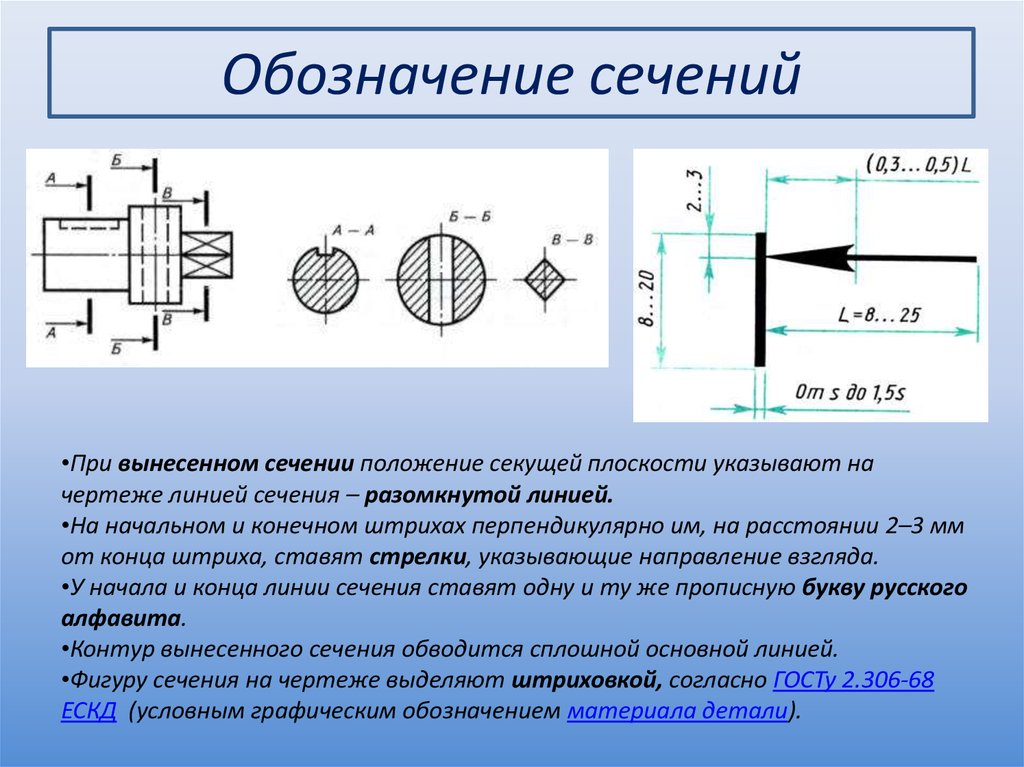
Для чего применяют сечение: Сечения применяют для выявления поперечной формы предмета. Разрезы применяют с целью выявления внутреннего устройства предмета
Содержание
ЧЕРЧЕНИЕ. Школьный интернет-учебник — Сечения и разрезы 4-1
Производственные чертежи содержат различные типы изображений — виды, сечения и разрезы. С видами на чертеже мы уже познакомились…
Сечения и разрезы позволяют выявить внешнюю и внутреннюю форму детали (рис.1, а, б). Названные изображения получают в результате мысленного рассечения детали секущей плоскостью, положение которой выбирают в зависимости от формы изображаемой детали.
Рис. 1. Сечение (а) и разрез (б)
Сечения и разрезы дополняют и уточняют геометрическую информацию о предмете и тем самым увеличивают возможности выявления формы изображаемого объекта на чертеже. В некоторых случаях они имеют большую информационную емкость, чем виды. Разрезы и сечения являются проекционными изображениями и выполняются по правилам прямоугольного проецирования.
Сечение — изображение фигуры, получающейся при мысленном рассечении предмета секущей плоскостью.
Образование сечения
Деталь мысленно рассекают секущей плоскостью в том месте, где необходимо уточнить форму изделия. В секущей плоскости получают фигуру сечения (рис.2).
Рис. 2. Образование сечения
Изображение сечения
После этого секущую плоскость (вместе с фигурой сечения) мысленно вынимают, поворачивают вокруг вертикальной оси, перемещают параллельно плоскости проекций и совмещают с фронтальной плоскостью так, чтобы изображения вида спереди и фигуры сечения не заслоняли друг друга. В сечении показывается только то, что находится в секущей плоскости.
Расположение сечений
В зависимости от расположения на чертеже сечения разделяют на:
а) вынесенные, когда сечения располагают в любом месте чертежа;
б) наложенные, когда их располагают непосредственно на виде предмета;
в) в разрыве — располагают в разрыве изображения.
Вынесенное и наложенное сечение показано на рис.3.
Рис.3. Построение сечений
Вынесенное сечение можно выполнять двумя способами:
1. если вид спереди находится в проекционной связи с сечением, то полученное изображение фигуры сечения называют сечением, выполненным в проекционной связи (рис.4).
Рис. 4. Сечение, выполненное в проекционной связи.
2. секущую плоскость с фигурой сечения допускается перемещать в произвольном направлении, совмещая ее с плоскостью проекций, без учета проекционной связи. Такое сечение называется сечением, выполненным на свободном месте чертежа (рис. 5).
Рис. 5. Сечение, выполненное на свободном месте чертежа.
Обозначение сечений
ГОСТ 2.305–68 устанавливает правила изображения и обозначения сечений.
При вынесенном сечении положение секущей плоскости указывают на чертеже линией сечения – разомкнутой линией, которая проводится в виде отдельных штрихов, не пересекающих контур соответствующего изображения. Толщина штрихов берётся в пределах от S до 1,5 S, а длина их от 8 до 20 мм. На начальном и конечном штрихах перпендикулярно им, на расстоянии 2–3 мм от конца штриха, ставят стрелки, указывающие направление взгляда (рис. 6).
Рис. 6. Взаимное расположение штрихов разомкнутой линии и стрелок
У начала и конца линии сечения ставят одну и ту же прописную букву русского алфавита. Буквенные обозначения присваиваются в алфавитном порядке без повторений и без пропусков, за исключением букв И, О, X, Ъ, Ы, Ь (рис. 4). Если для выявления формы деталей требуется выполнить несколько сечений, тогда проводят несколько разомкнутых линий, которые на чертеже продолжают обозначать следующими буквами русского алфавита (Б, В, Г и т. д.) (рис. 7).
д.) (рис. 7).
Рис. 7. Обозначение нескольких сечений
Контур вынесенного сечения обводится сплошной основной линией такой же толщины S, как видимый контур изображения. Фигуру сечения на чертеже выделяют штриховкой, согласно ГОСТу 2.306-68 ЕСКД (условным графическим обозначением материала детали). Штриховые линии наносят в соответствии с общими правилами (в основном тонкими линиями под углом 45° к основной надписи, в любом направлении через 2-3 мм). Над сечением пишут те же буквы через тире (типа А – А).
Если сечение представляет собой симметричную фигуру и располагается на продолжении линии сечения (штрихпунктирной), то стрелок и букв не наносят (см. рис. 5).
Наложенным называют сечение, которое располагают непосредственно на виде предмета в том месте, где проходила секущая плоскость, то есть, как бы накладывают на изображение. Наложенное сечение выполняется в том случае, когда форма детали на всём протяжении одинакова. Контур наложенного сечения обводят сплошной тонкой линией (от S/3 до S/2). Фигуру сечения располагают в том месте основного вида, где проходит секущая плоскость, и заштриховывают.
Контур наложенного сечения обводят сплошной тонкой линией (от S/3 до S/2). Фигуру сечения располагают в том месте основного вида, где проходит секущая плоскость, и заштриховывают.
Наложенное сечение тоже бывает двух видов:
1. если наложенное сечение симметрично относительно секущей плоскости, то на сечении указывается только ось штрихпунктирной линией без обозначения буквами и стрелками (рис. 8, а).
2. если наложенное сечение представляет собой несимметричную фигуру, то проводят разомкнутую линию с указанием стрелками направления взгляда, но буквами не обозначают (рис. 8, б).
Рис. 8. Наложенное сечение: а) симметричное; б) несимметричное.
Если сечение находится в разрыве между частями одного и того же вида, то его выполняют сплошной основной линией (рис. 9). Правила обозначения сечений, расположенных в разрыве, аналогичны правилам обозначений наложенных сечений: у симметричных сечений указывается только ось (рис. 9,а), а несимметричные сечения сопровождают указанием разомкнутой линии и стрелками, указывающими направление взгляда (рис. 9,б).
9,а), а несимметричные сечения сопровождают указанием разомкнутой линии и стрелками, указывающими направление взгляда (рис. 9,б).
Рис. 9. Сечения в разрыве: а) симметричное; б) несимметричное
Особенности выполнения
При выполнении сечений применяют следующие условности:
1. Вынесенным сечениям следует отдавать предпочтение перед наложенным, так как последние затемняют чертеж и неудобны для нанесения размеров.
2. При прохождении секущей плоскости через ось поверхности вращения, ограничивающей отверстие или углубление, контур отверстия или углубления в сечении показывают полностью (рис. 10).
Рис. 10. Сечение, проходящее через оси поверхностей вращения
3. Если секущая плоскость проходит через призматическое сквозное отверстие и фигура сечения распадается на несколько частей, сечение не выполняется (рис. 11).
11).
Рис. 11. Сечение, проходящее через призматическое сквозное отверстие.
4. Сечение, распадающееся на отдельные части, заменяют разрезом (рис. 12).
Рис. 12. Замена сечения разрезом
5. Сечения с линией контура под углом 45° штрихуются под углом 30°или 60° (рис. 13).
Рис. 13. Штриховка под углом 60°.
6. Для нескольких одинаковых сечений, относящихся к одному предмету, линию сечения обозначают одинаковыми буквами и вычерчивают одно сечение (рис. 14).
Рис. 14. Выполнение нескольких одинаковых сечений
7. Сечение можно располагать с поворотом, тогда к надписи А – А должен быть добавлен символ повёрнуто , то есть А – А . Если секущие плоскости нескольких одинаковых сечений не параллельны друг другу, то значок не наносится.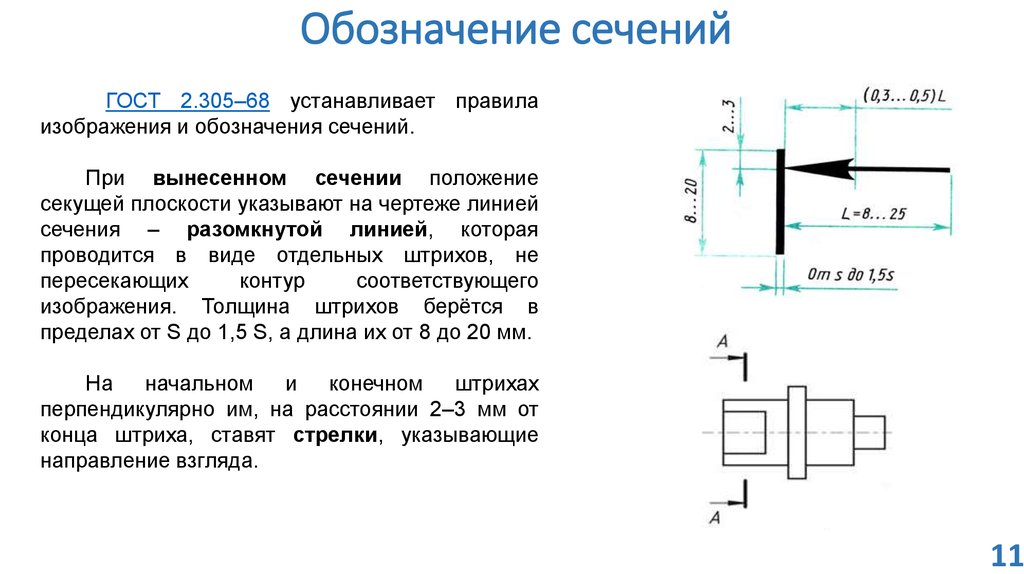
Сечения — Черчение
Производственные чертежи содержат различные типы изображений — виды, разрезы, сечения.
Сечения и разрезы позволяют выявить внешнюю и внутреннюю (рис. 147, а, б) форму детали. Названные изображения получают в результате мысленного рассечения детали секущей плоскостью, положение которой выбирают в зависимости от формы изображаемой детали. Сечения и разрезы дополняют и уточняют геометрическую информацию о предмете и тем самым увеличивают возможности выявления формы изображаемого объекта на чертеже. В некоторых случаях они имеют большую информационную емкость, чем виды. Разрезы и сечения являются проекционными изображениями и выполняются по правилам прямоугольного проецирования.
Рис. 147. Сечение (а) и разрез (б)
Сечение — изображение фигуры, получающейся при мысленном рассечении предмета секущей плоскостью.
Деталь проецируют на плоскость проекций V (рис. 148, а). Затем ее мысленно рассекают секущей плоскостью в том месте, где необходимо уточнить форму изделия. В секущей плоскости получают фигуру сечения. После этого секущую плоскость (вместе с фигурой сечения) мысленно вынимают, поворачивают вокруг вертикальной оси, перемещают параллельно плоскости проекций и совмещают с плоскостью V так, чтобы изображения вида спереди и фигуры сечения не заслоняли друг друга (рис. 148, б). Обратите внимание на то, что при таком перемещении секущей плоскости вид спереди находится в проекционной связи с сечением. Полученное изображение фигуры сечения называют сечением, выполненным в проекционной связи.
Секущую плоскость с фигурой сечения допускается перемещать в произвольном направлении, совмещая ее с плоскостью проекций, без учета проекционной связи. Такое сечение называется сечением, выполненным на свободном месте чертежа (рис.
Если сечение располагается на продолжении следа секущей плоскости, то сечение не обозначается (см. рис. 148, г). Если сечение располагается на свободном месте чертежа, то его обозначают надписью типа «А — А» (см. рис. 148, б, в).
Если секущая плоскость проходит вдоль оси цилиндрической или фонической поверхности, ограничивающих отверстие или углубление, то их контур на сечении показывают полностью, например изображение углубления конической формы (см. рис. 148).
Для выявления формы некоторых деталей иногда требуется выполнить несколько сечений, которые на чертеже обозначают буквами русского алфавита (рис. 149).
ГОСТ 2.305—68 устанавливает правила изображения и обозначения сечений.
Контуры фигуры сечения детали изображают сплошной основной линией.
Рис. 148. Сечения:
а — получение сечения; б — сечение, построенное в проекционной связи с видом; в — сечение, выполненное на свободном месте чертежа; г — сечение, выполненное на продолжении следа секущей плоскости
Рис. 149. Обозначение сечений буквами русского алфавита
12. Графические обозначения некоторых материалов на чертежах
|
Почему поперечные сечения имеют значение в колледже технического дизайна
В рамках программы «Технологии архитектурного проектирования» цифровой школы вы будете работать над различными способами передачи планов проекта с использованием цифровых чертежей. Поперечные разрезы или разрезы, как их обычно называют, представляют собой архитектурные чертежи, представляющие собой ортогональные проекции конструкций с разрезом, пересекающим их. Этот тип проекции показывает трехмерный рисунок в двухмерном виде. Разрез обычно вертикальный и показывает детали, которые горизонтальный разрез на чертеже разреза в плане не может показать.
Поперечные разрезы или разрезы, как их обычно называют, представляют собой архитектурные чертежи, представляющие собой ортогональные проекции конструкций с разрезом, пересекающим их. Этот тип проекции показывает трехмерный рисунок в двухмерном виде. Разрез обычно вертикальный и показывает детали, которые горизонтальный разрез на чертеже разреза в плане не может показать.
Двухмерное качество поперечного сечения позволяет включить больше информации, чем трехмерная концепция. Как правило, для проектов требуется несколько поперечных сечений, число которых увеличивается в зависимости от сложности проекта. С помощью BIM вы можете создавать поперечные сечения всех видов, выбирая плоскости сечения на 3D-модели. Прочтите, чтобы узнать больше о том, почему поперечные сечения важны для вашего образования и карьеры.
Программы технического проектирования показывают, как поперечные сечения предоставляют полезную информацию
Поперечные сечения облегчают построение планов, предоставляя более подробную информацию как о конструкции, так и о ограждении. По мере того, как конструкции становятся более сложными и имеют больше деталей, становится необходимым больше поперечных сечений с различными видами. Они позволяют разрезать здания, стены, лестничные пролеты или другие детали и давать точное изображение материалов и конструкций, которые трудно увидеть иначе.
По мере того, как конструкции становятся более сложными и имеют больше деталей, становится необходимым больше поперечных сечений с различными видами. Они позволяют разрезать здания, стены, лестничные пролеты или другие детали и давать точное изображение материалов и конструкций, которые трудно увидеть иначе.
Поперечные сечения могут прорезать потолки, полы и даже использоваться для лепнины и отделочных работ. Программы технического проектирования, которые дают вам обучение BIM, позволяют вам увидеть, сколько информации видно, когда вы создаете поперечное сечение из модели. В сочетании с фасадами, которые показывают стороны конструкции, не разрезая их, команда может понять как концепцию дизайна, так и логику, которая поможет воплотить его в жизнь.
Команда способна понять логику конструкции с поперечными сечениями
Ограждения становятся понятнее с поперечными сечениями
Ограждения зданий — это части, которые отделяют внутреннее пространство от внешнего. К ним относятся стены, крыши, окна и двери, а также фундамент.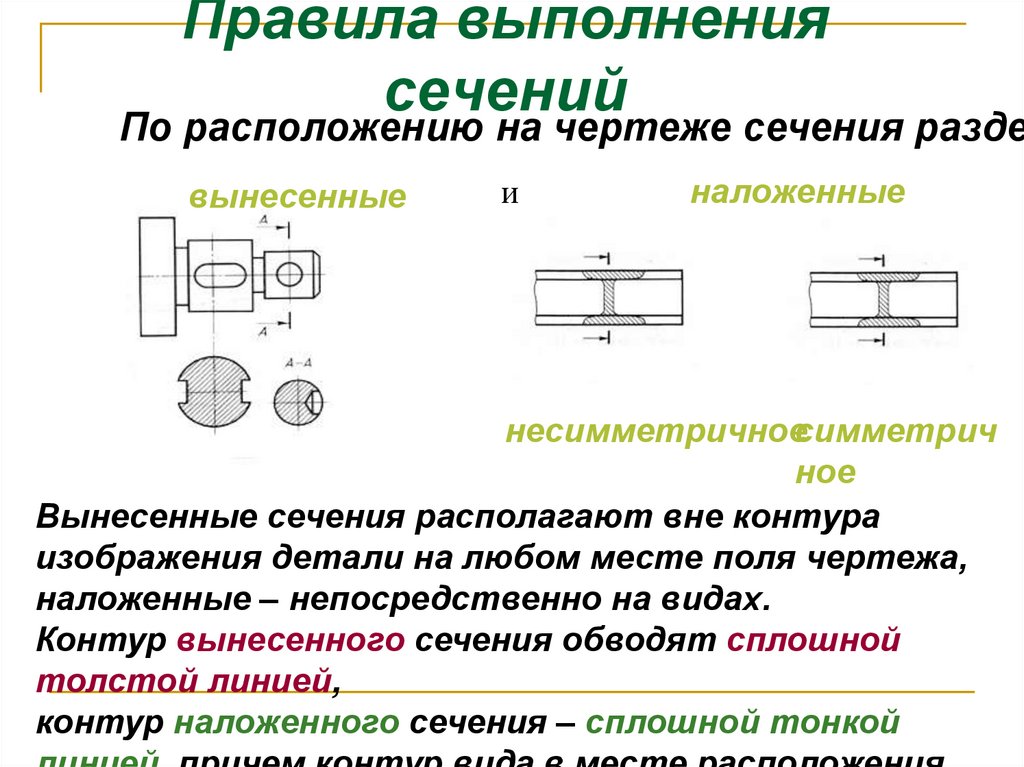 Иногда это называют «оболочкой здания». Эти компоненты защищают интерьер от физических элементов внешнего пространства, таких как погода, температура и солнечный свет. Если вы проходите обучение технологиям архитектурного проектирования, вы уже знаете, насколько важны эти конструкции для успешного функционирования пространства. Чем яснее эти элементы могут быть представлены строителям, тем эффективнее может быть построен план. Размеры и слои легко выявляются на поперечном сечении, поэтому тонкости построения корпусов становятся более очевидными.
Иногда это называют «оболочкой здания». Эти компоненты защищают интерьер от физических элементов внешнего пространства, таких как погода, температура и солнечный свет. Если вы проходите обучение технологиям архитектурного проектирования, вы уже знаете, насколько важны эти конструкции для успешного функционирования пространства. Чем яснее эти элементы могут быть представлены строителям, тем эффективнее может быть построен план. Размеры и слои легко выявляются на поперечном сечении, поэтому тонкости построения корпусов становятся более очевидными.
Измерения легче обозначать на поперечных сечениях
Четко обозначенные измерения бесспорно важны в архитектурных технологиях. Когда измерения неточны, время, деньги и энергия тратятся впустую. Без поперечных сечений трудно отметить многие размеры, которые находятся внутри конструкции или в ограждениях. Если вы уже учитесь в колледже технического дизайна, то, вероятно, уже знаете, насколько важна точность и внимание к деталям при планировании зданий.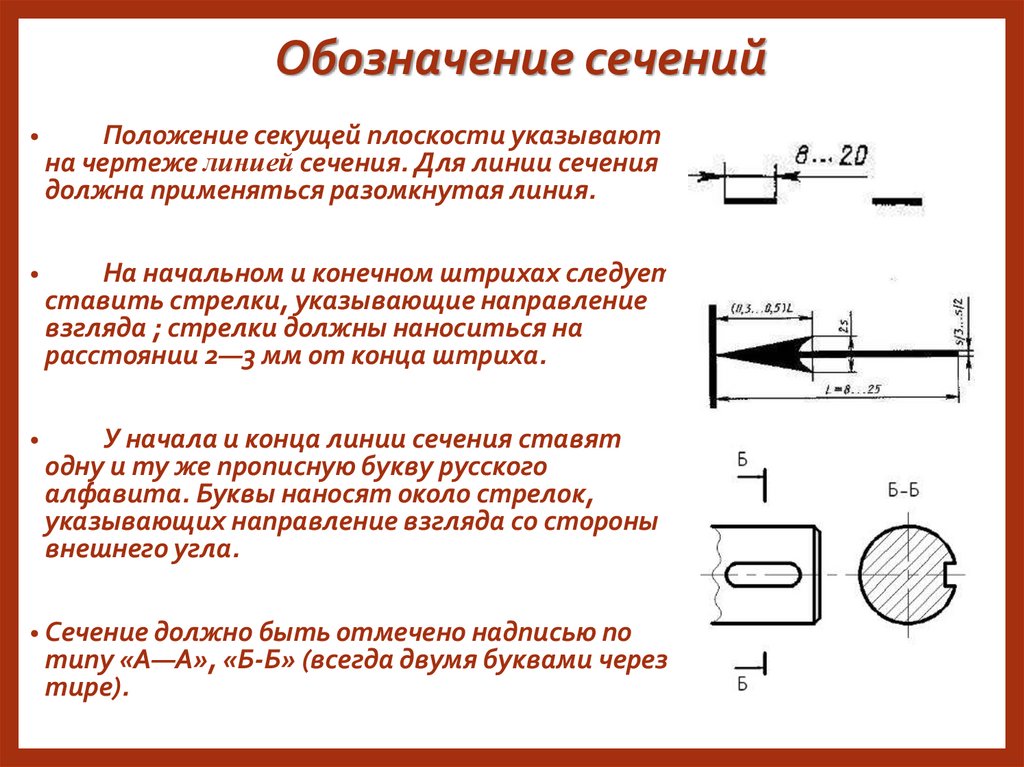
В ходе своей карьеры вы сможете рассчитывать на возможности BIM по включению огромных объемов данных для обеспечения бесперебойной работы проектов. С помощью BIM вы можете легко манипулировать и изменять цифровые чертежи и поперечные сечения, и эти изменения сразу же видны различным командам, работающим над одним и тем же проектом. Отчасти поэтому BIM так изменила проектирование и строительство зданий, и почему изучение BIM даст вам ценные навыки для вашей карьеры.
Хотите узнать больше о технологиях архитектурного проектирования?
Вас ждет карьера.
Свойства поперечного сечения | МеханиКальк
База данных
Справочник по инструкциям
База данных поперечных сечений
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
Поведение элемента конструкции определяется его материалом и геометрией. Эта ссылка посвящена влиянию геометрии на поведение элемента конструкции. Поперечное сечение и длина элемента конструкции влияют на то, насколько этот элемент прогибается под нагрузкой, а поперечное сечение определяет напряжения, которые существуют в элементе под данной нагрузкой.
Свойства областей
Центроид
Центроид формы представляет собой точку, вокруг которой равномерно распределена площадь сечения. Если область дважды симметрична относительно двух ортогональных осей, центр тяжести лежит на пересечении этих осей. Если область симметрична только относительно одной оси, то центроид лежит где-то вдоль этой оси (необходимо вычислить другую координату). Если точное местоположение центроида не может быть определено осмотром, его можно рассчитать следующим образом:
где dA представляет собой площадь бесконечно малого элемента, A представляет собой общую площадь поперечного сечения, а x и y представляют собой координаты элемента dA относительно оси интереса.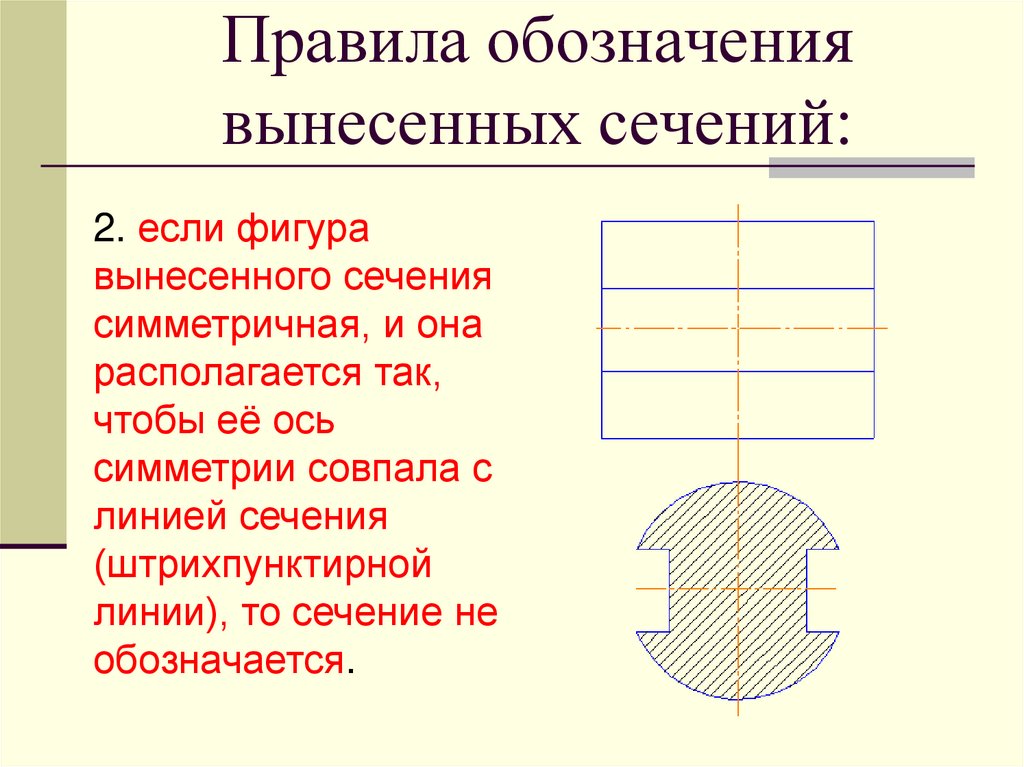
Центроидальное расположение общих поперечных сечений хорошо задокументировано, поэтому обычно нет необходимости вычислять местоположение с помощью приведенных выше уравнений.
Если поперечное сечение состоит из набора основных форм, центральные положения которых известны относительно некоторой контрольной точки, то центральное положение составного поперечного сечения можно рассчитать как:
где x c,i и y c,i — прямоугольные координаты центра тяжести сечения i th относительно опорной точки, а A i — площадь i th раздел.
Центральное расстояние
центроидальное расстояние , с, является расстоянием от центра тяжести поперечного сечения до крайней точки волокна. Центроидальное расстояние в направлении Y для прямоугольного поперечного сечения показано на рисунке ниже:
Обычное использование центроидального расстояния включает:
- расчет максимального напряжения изгиба в поперечном сечении
- расчет значения первого момента площади Q над точкой в поперечном сечении для определения напряжения сдвига в этой точке
Первый момент области
Первый момент площади указывает распределение площади относительно некоторой оси. Первый момент площади относительно интересующей оси рассчитывается как:
Первый момент площади относительно интересующей оси рассчитывается как:
| Q x = ∫ y дА | Q y = ∫ x dA |
где Q x — первый момент относительно оси x, а Q y — первый момент относительно оси y. Значения x и y указывают положение относительно оси интереса бесконечно малых площадей dA каждого элемента при выполнении интегрирования.
Если область состоит из набора основных форм, центроидальные положения которых известны относительно интересующей оси, то первый момент составной области можно рассчитать как:
Если вы сравните приведенные выше уравнения для Q с уравнениями для расчета центроида (обсуждаемыми в предыдущем разделе), вы увидите, что мы фактически используем первый момент площади при расчете центроидального местоположения относительно интересующего источника.
Первый момент также используется при расчете величины касательного напряжения в той или иной точке поперечного сечения.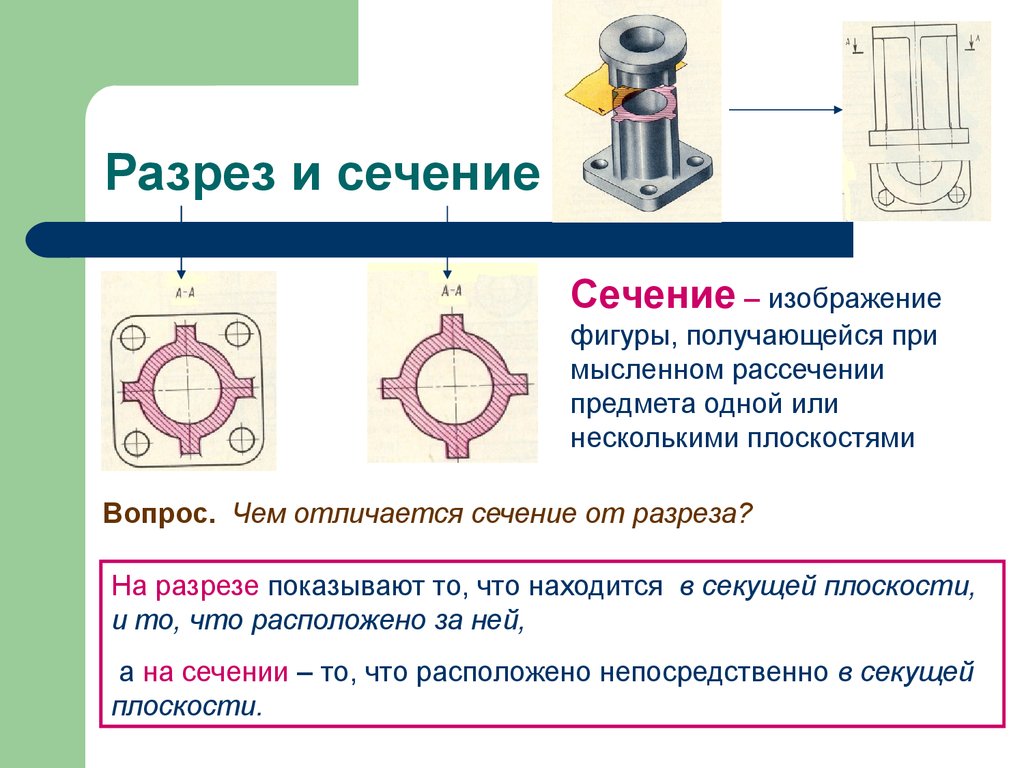 Напомним, что касательное напряжение в любой точке, расположенной на расстоянии y 1 от центра тяжести поперечного сечения рассчитывается как:
Напомним, что касательное напряжение в любой точке, расположенной на расстоянии y 1 от центра тяжести поперечного сечения рассчитывается как:
где Q — первый момент площади между точкой y 1 и крайним волокном (верхним или нижним) сечения. Рассмотрим рисунок ниже. Нас интересует расчет касательного напряжения в точке, расположенной на расстоянии y 1 от центра тяжести поперечного сечения. Мы можем рассчитать первый момент площади выше или ниже этого местоположения. В этом случае точка интереса находится выше нейтральной оси, поэтому проще рассмотреть верхнюю область, которая на рисунке ниже заштрихована синим цветом. Эта область простирается от точки y 1 до крайнего волокна в верхней части поперечного сечения.
Первый момент относительно оси x области, заштрихованной синим цветом на рисунке выше, рассчитывается относительно центра тяжести поперечного сечения (точка O на рисунке) как:
Если центроидальное расположение интересующей области известно, то первый момент области относительно центроида упрощается до (см.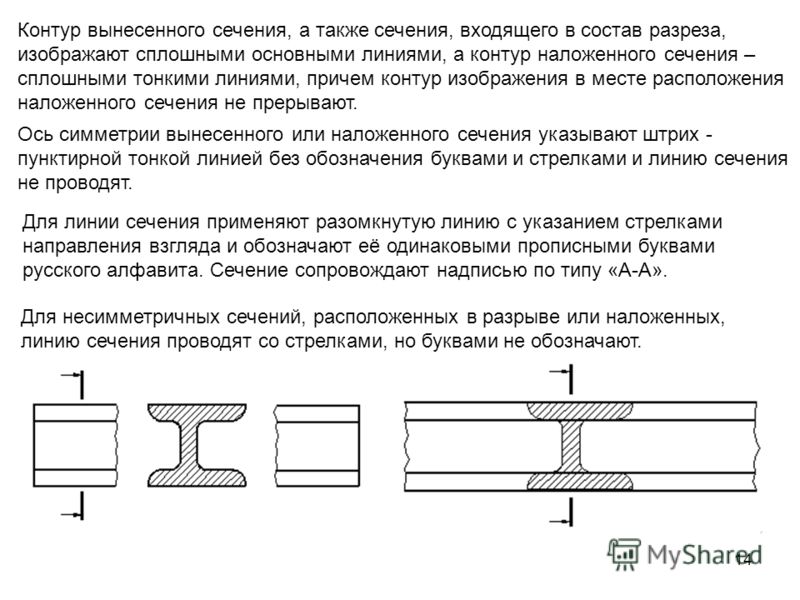 Рисунок выше):
Рисунок выше):
Q сх = у с1 А 1
Следует отметить, что первый момент области может быть либо положительным, либо отрицательным в зависимости от положения области относительно оси интереса. Следовательно, первый момент всей площади поперечного сечения относительно его собственного центроида равен нулю.
Площадь Момент инерции
Второй момент площади, более известный как момент инерции , I поперечного сечения, является показателем способности элемента конструкции сопротивляться изгибу. (Примечание 1) I x и I y — моменты инерции относительно осей x и y, соответственно, и рассчитываются по формуле:
| I x = ∫ y 2 дА | I y = ∫ x 2 да |
где x и y — координаты элемента dA относительно оси интереса.
Чаще всего моменты инерции рассчитываются относительно центра тяжести сечения.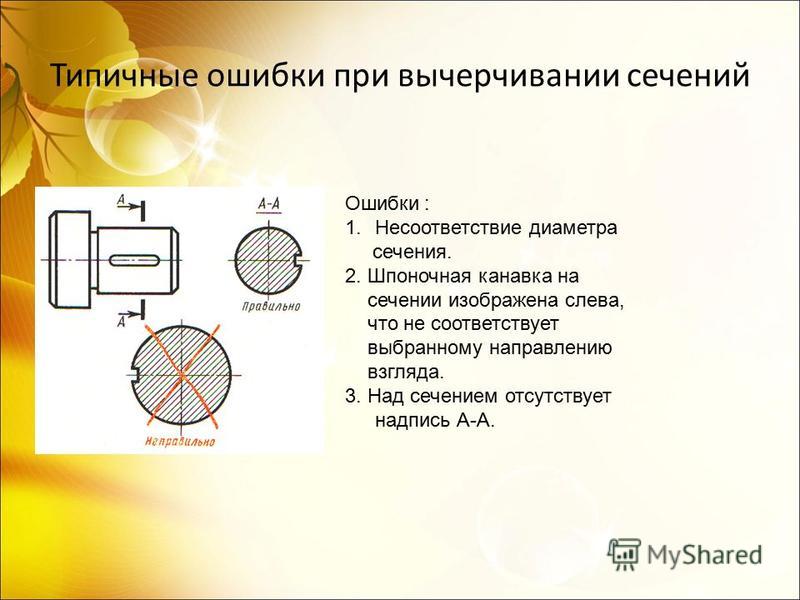 В этом случае они обозначаются как центроидальных моментов инерции и обозначаются как I cx для инерции относительно оси x и I cy для инерции относительно оси y.
В этом случае они обозначаются как центроидальных моментов инерции и обозначаются как I cx для инерции относительно оси x и I cy для инерции относительно оси y.
Моменты инерции обычных поперечных сечений хорошо задокументированы, поэтому обычно нет необходимости рассчитывать их с помощью приведенных выше уравнений. Свойства нескольких общих сечений приведены в конце этой страницы.
Если поперечное сечение состоит из набора основных форм, все центроиды которых совпадают, то момент инерции составного сечения представляет собой просто сумму отдельных моментов инерции. Примером этого является коробчатая балка, состоящая из двух прямоугольных секций, как показано ниже. В этом случае внешняя секция имеет «положительную площадь», а внутренняя секция имеет «отрицательную площадь», поэтому составной момент инерции представляет собой вычитание момента инерции внутренней секции из внешней секции.
В случае более сложного составного поперечного сечения, в котором центральные положения не совпадают, момент инерции можно рассчитать с использованием теоремы о параллельности осей .
Важно не путать момент инерции площади с массовым моментом инерции твердого тела. Момент инерции площади указывает на сопротивление поперечного сечения изгибу, тогда как момент инерции массы указывает на сопротивление тела вращению.
Теорема о параллельных осях
Если известен момент инерции поперечного сечения относительно центральной оси, то можно использовать теорему о параллельной оси для расчета момента инерции относительно любой параллельной оси:
I параллельная ось = I c +плюс; А д 2
где I c — момент инерции относительно центральной оси, d — расстояние между центральной осью и параллельной осью, а A — площадь поперечного сечения.
Если поперечное сечение состоит из набора основных фигур, центроидальные моменты инерции которых известны вместе с расстояниями от центроидов до некоторой контрольной точки, то теорему о параллельных осях можно использовать для расчета момента инерции составного поперечного сечения.
Например, двутавровая балка может быть аппроксимирована тремя прямоугольниками, как показано ниже. Поскольку это составное сечение симметрично относительно осей x и y, центр тяжести сечения может быть расположен путем осмотра на пересечении этих осей. Центроид расположен в начале координат O на рисунке.
Момент инерции составного сечения можно рассчитать, используя теорему о параллельных осях. Центроидальный момент инерции секции относительно оси x I cx рассчитывается как:
I cx.IBeam = I cx.W +плюс; ( I cx.F1 + A F1 d 1 2 ) + ( I cx.F2 + A F2 d 2 2 )
где я 9Члены 0075 cx представляют собой моменты инерции отдельных сечений относительно их собственных центроидов при ориентации оси x, члены d представляют собой расстояния центроидов отдельных сечений до центроида составного сечения, а члены A равны площади отдельных секций. Поскольку центроид сечения W и центроид составного сечения совпадают, d равно нулю для этого сечения, и поэтому член Ad 2 отсутствует.
Поскольку центроид сечения W и центроид составного сечения совпадают, d равно нулю для этого сечения, и поэтому член Ad 2 отсутствует.
Важно отметить следствие теоремы о параллельности осей, заключающееся в том, что по мере удаления отдельной секции от центра тяжести составной секции вклад этой секции в момент инерции составной секции увеличивается в d 9 раз.0079 2 . Следовательно, если целью является увеличение момента инерции секции относительно определенной оси, наиболее эффективно расположить область как можно дальше от этой оси. Это объясняет форму двутавровой балки. Фланцы вносят основной вклад в момент инерции, а перегородка служит для отделения фланцев от оси изгиба. Однако перемычка должна сохранять некоторую толщину, чтобы избежать коробления, а также потому, что перемычка принимает на себя значительную часть напряжения сдвига в сечении.
Полярный момент инерции
Полярный момент инерции , Дж, поперечного сечения является показателем способности элемента конструкции сопротивляться кручению вокруг оси, перпендикулярной сечению. Полярный момент инерции сечения относительно оси можно рассчитать по формуле:
Полярный момент инерции сечения относительно оси можно рассчитать по формуле:
J = ∫ r 2 dA = ∫ (x 2 + y 2 ) dA
где x и y — координаты элемента dA относительно оси интереса, а r — расстояние между элементом dA и осью интереса.
Хотя полярный момент инерции можно рассчитать с помощью приведенного выше уравнения, обычно удобнее вычислять его с помощью теоремы о перпендикулярной оси , которая утверждает, что полярный момент инерции площади представляет собой сумму моментов инерции относительно любые две ортогональные оси, проходящие через интересующую ось:
Дж = I x + я г
Чаще всего ось интереса проходит через центр тяжести поперечного сечения.
Модуль упругости сечения
Максимальное изгибающее напряжение в балке рассчитывается как σ b = Mc / I c , где c — расстояние от нейтральной оси до крайнего волокна, I c — центроидальный момент инерции, а M — изгибающий момент. Модуль сопротивления объединяет члены c и I c в уравнении напряжения изгиба:
Модуль сопротивления объединяет члены c и I c в уравнении напряжения изгиба:
S = I с / с
Используя модуль сечения, напряжение изгиба рассчитывается как σ b = M / S. Полезность модуля сечения заключается в том, что он характеризует сопротивление поперечного сечения изгибу в одном выражении. Это позволяет оптимизировать поперечное сечение балки для сопротивления изгибу за счет максимизации одного параметра.
Радиус вращения
Радиус вращения представляет собой расстояние от центра тяжести сечения, на котором вся площадь может быть сосредоточена без какого-либо влияния на момент инерции. Радиус вращения формы относительно каждой оси определяется выражением:
Полярный радиус вращения также можно рассчитать для задач, связанных с кручением вокруг центральной оси:
Прямоугольные радиусы вращения также можно использовать для расчета полярного радиуса вращения:
r p 2 = r x 2 +плюс; р у 2
PDH Classroom предлагает курс повышения квалификации, основанный на этой справочной странице поперечных сечений. Этот курс можно использовать для выполнения кредитных требований PDH для поддержания вашей лицензии PE.
Этот курс можно использовать для выполнения кредитных требований PDH для поддержания вашей лицензии PE.
Теперь, когда вы прочитали эту справочную страницу, заработайте за это признание!
Просмотреть курс сейчас:
Просмотреть курс
Свойства общих сечений
В таблице ниже приведены свойства обычных поперечных сечений. Более подробные таблицы можно найти в перечисленных ссылках.
Свойства, рассчитанные в таблице, включают площадь, центральный момент инерции, модуль сечения и радиус вращения.
| Форма | Представительство | Свойства | ||
|---|---|---|---|---|
| Прямоугольник |
| |||
| Круг | ||||
| Круглая трубка | ||||
| Двутавровая балка |
Примечания
Примечание 1: Прогиб балки
Прогиб балки при изгибе определяется моментом инерции поперечного сечения, длиной балки и модулем упругости материала.
 В сечении показывается только то, что находится в секущей плоскости.
В сечении показывается только то, что находится в секущей плоскости.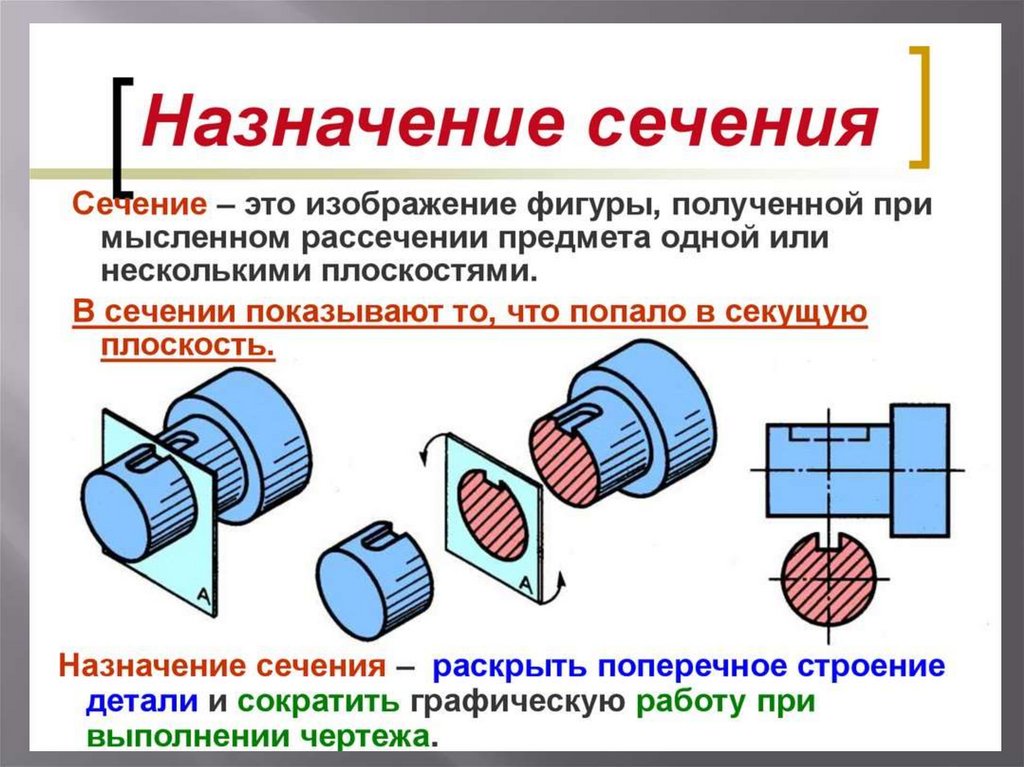 148, в). Сечение можно располагать и на продолжении следа секущей плоскости (рис. 148, г). Оно называется сечением, выполненным на продолжении следа секущей плоскости.
148, в). Сечение можно располагать и на продолжении следа секущей плоскости (рис. 148, г). Оно называется сечением, выполненным на продолжении следа секущей плоскости.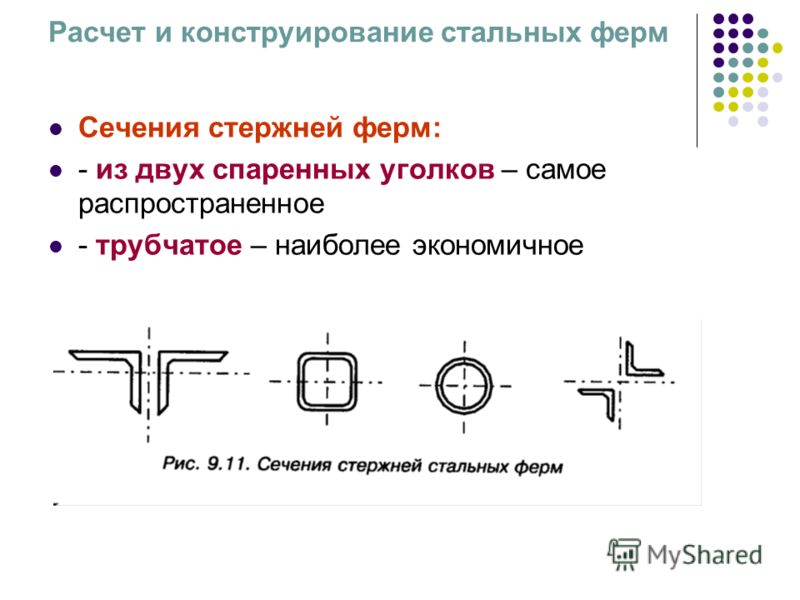 Внутри этих контуров дают условное графическое обозначение материала детали (табл. 12).
Внутри этих контуров дают условное графическое обозначение материала детали (табл. 12).