Как делать сечение в геометрии: Построение сечений

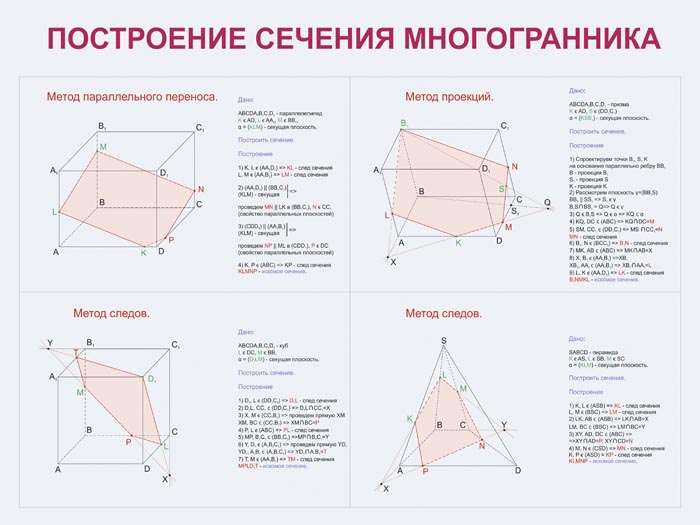
«Построение сечений в многогранниках методом следов». 10-й класс

• Апрелкова Татьяна Петровна

Разделы:

Математика

Класс:
10

Девиз: “Мы одна семья, мы учимся
все вместе”

Цели урока:

• Формирование у учащихся навыков решения задач
  на построение сечений методом следов.
• Формирование и развитие у учащихся
  пространственного воображения.
• Развитие графической культуры и математической
  речи.

Обучающая цель: формирование умений и
навыков построения сечений методом следов.

Воспитывающая цель: воспитывать чувство
сплоченности, взаимопомощи, воспитывать умения
работать индивидуально над задачей.

Тип урока: урок формирования и
совершенствования знаний.

Формы организации учебной деятельности:
групповая, индивидуальная, коллективная.

Техническое обеспечение урока:
мультимедийный проектор, набор геометрических
тел (куб, параллелепипед, пирамида).

Структура урока:

Ход урока

Организационный момент: Рассаживаемся на 3
группы по 5 человек. На каждом столе – набор тел,
памятки-опоры, карточки для индивидуальной
работы по построению сечений.

Слово учителя: Вы изучили аксиомы
стереометрии, следствия из аксиом, теоремы о
параллельности прямых и плоскостей в
пространстве. При решении многих
стереометрических задач используют сечение
многогранника плоскостью. Существует несколько
методов построения сечений многогранника
плоскостью: метод следов, метод внутреннего
проектирования и комбинированный метод.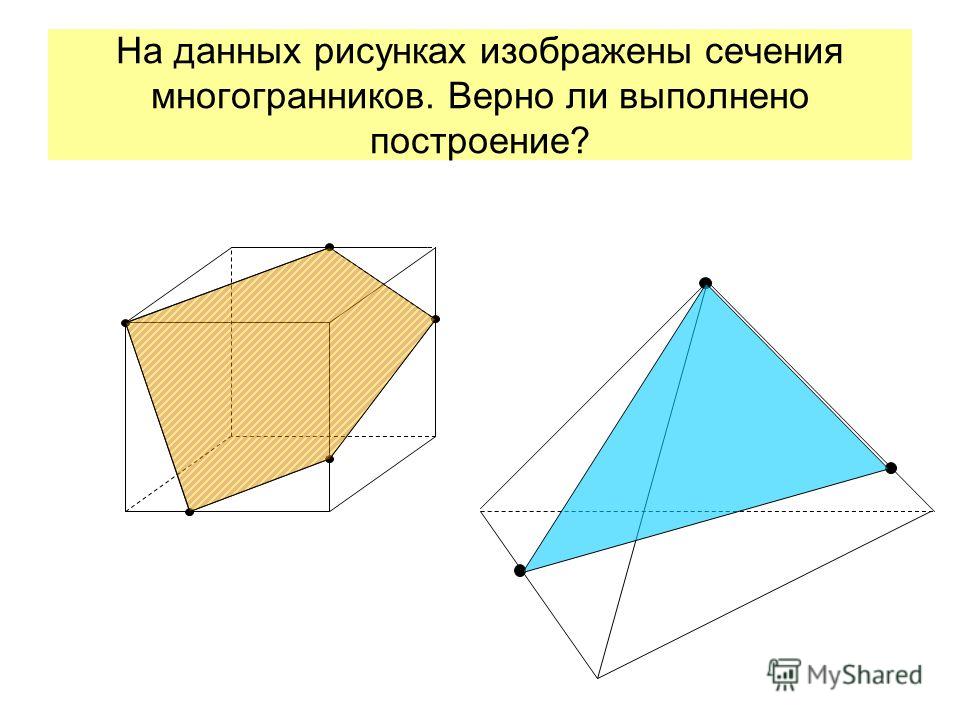

Мы изучим метод следов.

1) Ребята, я предлагаю вам повторить и
вспомнить некоторые геометрические понятия и
определения.

1. Основное понятие геометрии – место пересечения
   двух прямых, не имеющее измерения.
2. Геометрическая фигура, состоящая из шести
   квадратных граней.
3. Отдельный предмет в пространстве.
4. Способ изображения пространственных фигур на
   плоскость.
5. Плоская фигура, образуемая пересечением тела
   плоскостью.
6. Сторона грани многогранника.
7. Многогранник, поверхность которого состоит из
   четырех треугольников.

Ответы:

1. Точка
2. Куб
3. Тело
4. Проекция
5. Сечение
6. Ребро
7. Тетраэдр

2) Ребята, перед вами пример неправильного
построения сечения куба АС1 плоскостью,
проходящей через заданные точки N, C, D1.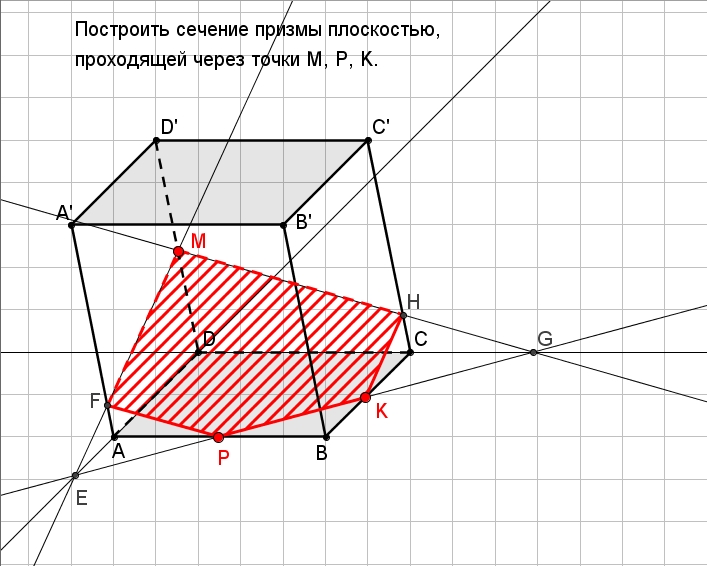

А рядом сечение построено верно.

На уроках черчения вы пользовались
определением: Сечение – это изображение
фигуры, которая получается при мысленном
рассечении тела плоскостью.

Вот таким определением мы и будем пользоваться
сегодня на уроке.

В тетраэдре сечениями могут быть только
треугольники или четырехугольники, а в
параллелепипеде – треугольники,
четырехугольники, пятиугольники или
шестиугольники.

Метод следов включает три важных пункта:

1. Строится линия пересечения (след) секущей
   плоскости с плоскостью основания многогранника.
2. Находим точки пересечения секущей плоскости с
   ребрами многогранника.
3. Строим и заштриховываем сечение.

Рассмотрим пример (мультимедийный проектор).

Построить сечение куба, проходящее через точки
М, N, L.

Алгоритм построения

1)

2)

3)

4)

5)

6)

7)

Задания группам построить сечение

Три ученика работают у доски (по одному
ученику из каждой группы)!

Опора-памятка

• Аксиома₁. Через любые три точки, не
  лежащие на одной прямой, проходит плоскость, и
  причем только одна.
• Аксиома₂. Если две точки прямой лежат в
  плоскости, то все точки прямой лежат в этой
  плоскости.
• Аксиома₃. Если 2 плоскости имеют общую
  точку, то они имеют общую прямую, на которой лежат
  все общие точки этих плоскостей.

Следствия из аксиом:

1. Через прямую и не лежащую на ней точку проходит
   плоскость, и притом только одна.
2. Через две пересекающиеся прямые проходит
   плоскость, и притом только одна.

Способы задания плоскости.

Итог урока: повторить алгоритм построения
сечения методом следов. Оценить работу учащихся.

Домашнее задание: закончить задания по
индивидуальным карточкам.

Презентация

20.12.2006

Построение сечений многогранников. Задачи — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Задачи на построение сечений

Цель работы:
Развитие пространственных представлений.
Задачи:
1. Познакомить с правилами построения сечений.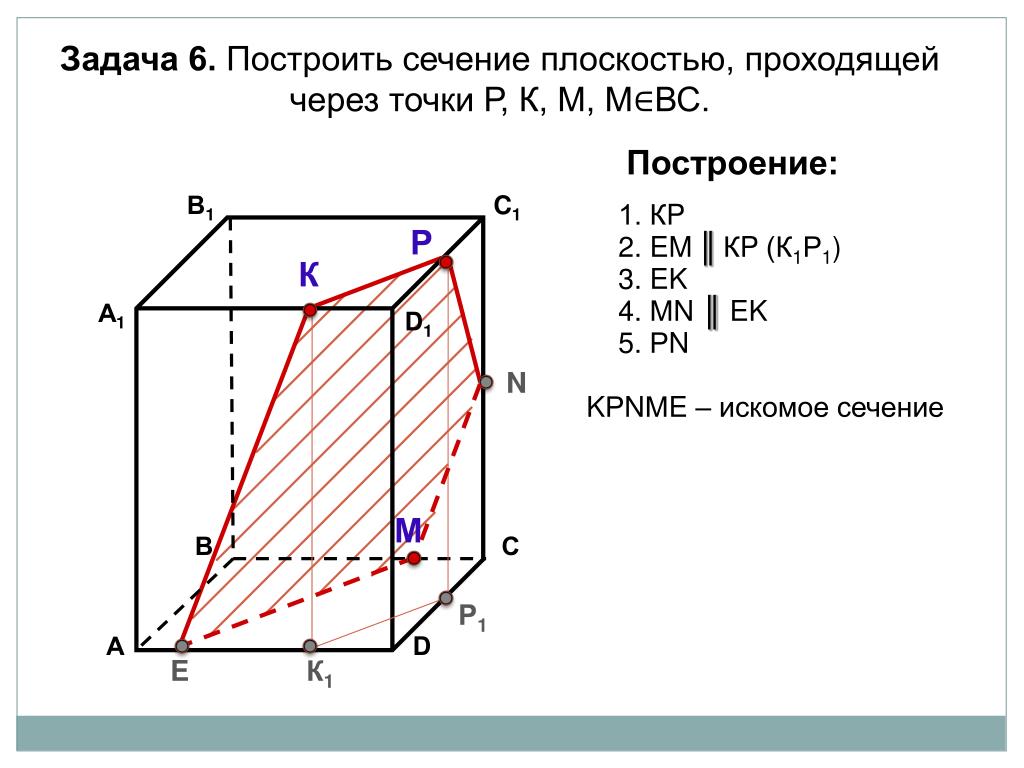
2. Выработать навыки построения сечений
тетраэдра и параллелепипеда при различных
случаях задания секущей плоскости.
3. Сформировать умение применять правила
построения сечений при решении задач по
темам «Многогранники».
Для решения многих
геометрических
задач необходимо
строить сечения
многогранников
различными
плоскостями.

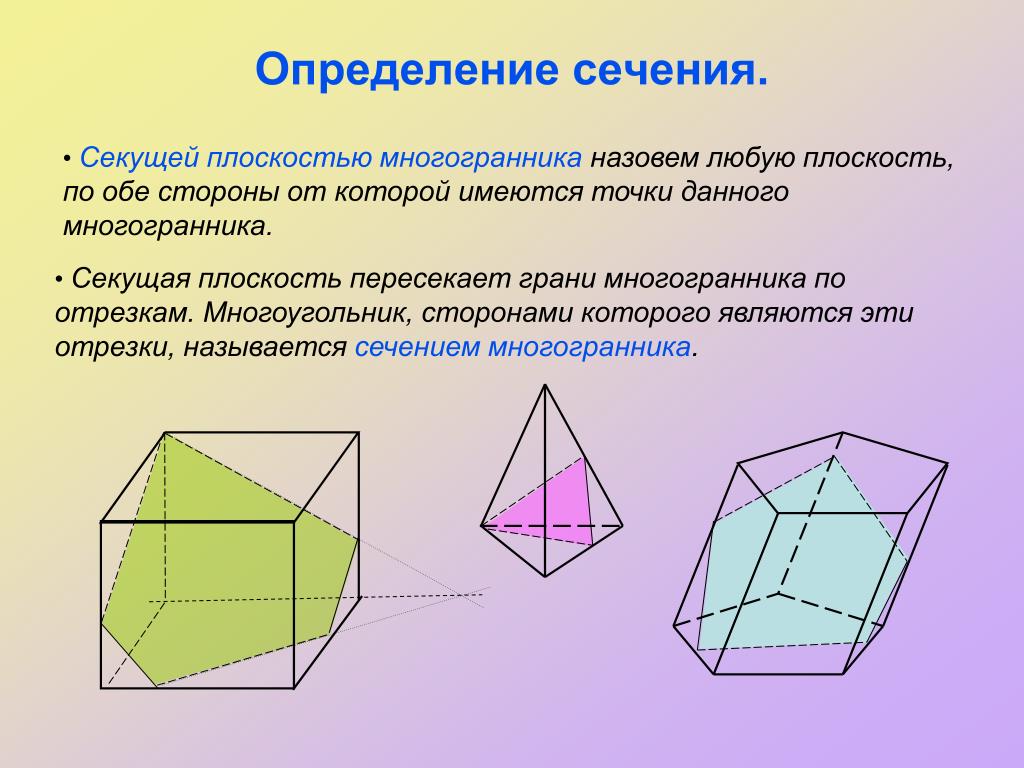
4. Понятие секущей плоскости

Секущей
плоскостью
параллелепипеда
(тетраэдра)
называется любая
плоскость, по обе
стороны от
которой имеются
точки данного
параллелепипеда
(тетраэдра).

5. Понятие сечения многогранника

Секущая плоскость
пересекает грани
тетраэдра
(параллелепипеда) по
отрезкам.
Многоугольник,
сторонами которого
являются данные
отрезки, называется
сечением тетраэдра
(параллелепипеда).

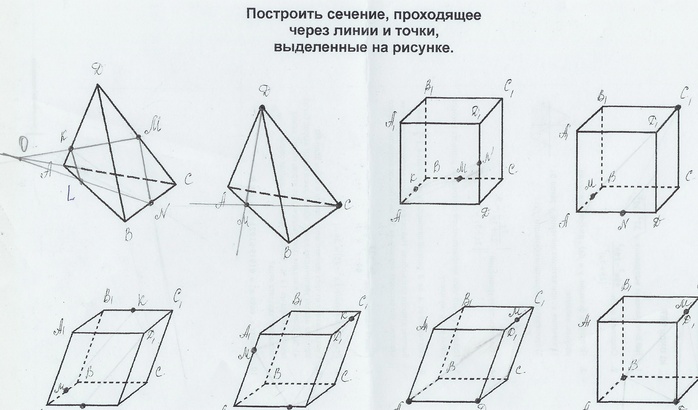
6. Работа по рисункам

Сколько плоскостей можно провести
через выделенные элементы?
Какие аксиомы и теоремы вы применяли?
Для построения сечения
нужно построить точки
пересечения секущей
плоскости с ребрами и
соединить их отрезками.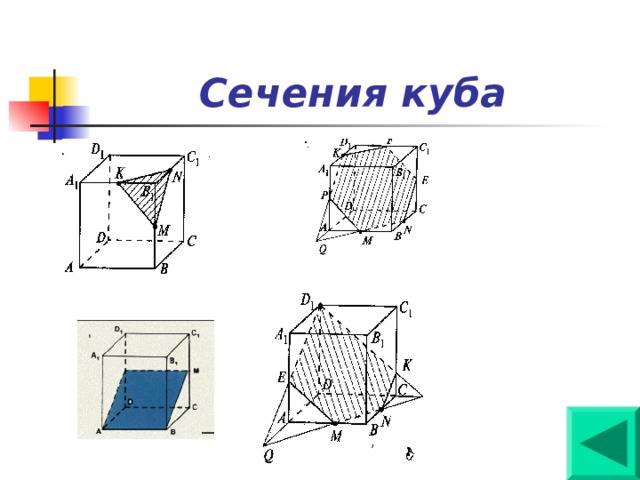

8. Правила построения сечений

1. Соединять можно только две
точки, лежащие в плоскости одной
грани.
2. Секущая плоскость пересекает
параллельные грани по
параллельным отрезкам.

9. Правила построения сечений

3. Если в плоскости грани отмечена
только одна точка, принадлежащая
плоскости сечения, то надо
построить дополнительную точку.
Для этого необходимо найти точки
пересечения уже построенных
прямых с другими прямыми,
лежащими в тех же гранях.

10. Построение сечений тетраэдра

Тетраэдр имеет 4 грани
В сечениях могут получиться
Треугольники
Четырехугольники
Построить сечение тетраэдра
DABC плоскостью, проходящей
через точки M,N,K
1. Проведем прямую через
точки М и К, т.к. они лежат
в одной грани (АDC).
D
M
AA
N
K
BB
CC
2. Проведем прямую через
точки К и N, т.к. они
лежат в одной грани
(СDB).
3. Аналогично рассуждая,
проводим прямую MN.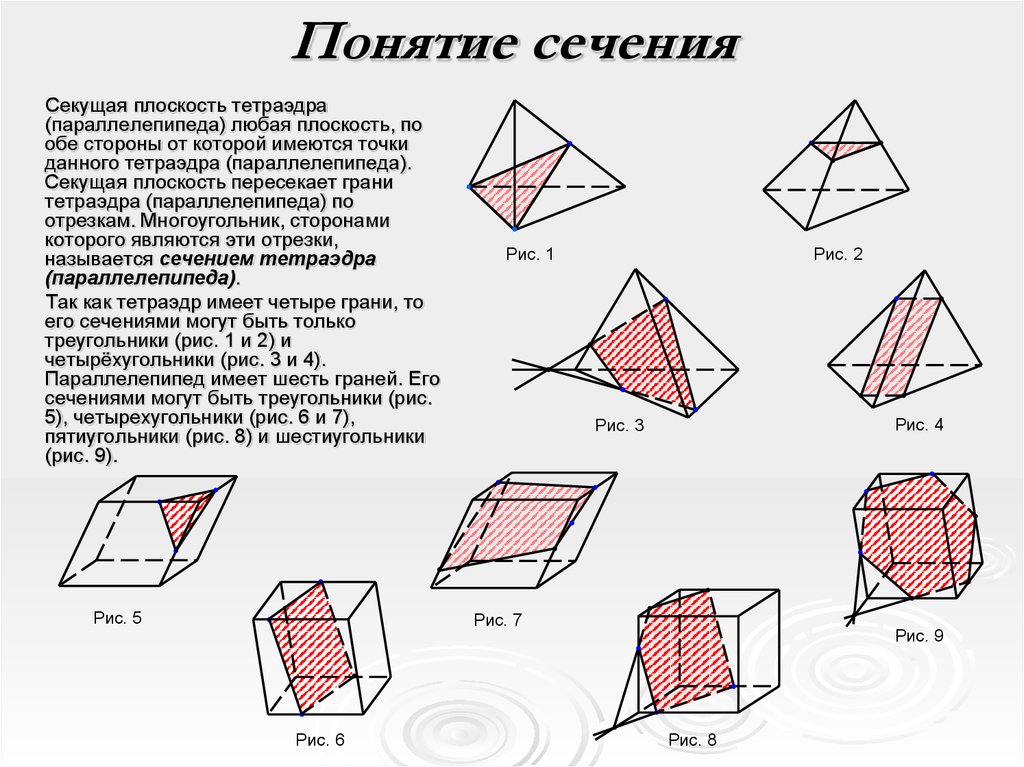
4. Треугольник MNK –
искомое сечение.

13. Построить сечение тетраэдра плоскостью, проходящей через точку М параллельно АВС.

D
1. Проведем через точку М
прямую параллельную
ребру AB
2.
М
Р
А
К
С
В
Проведем через точку М
прямую параллельную
ребру AC
3. Проведем прямую через
точки K и P, т.к. они лежат в
одной грани (DBC)
4. Треугольник MPK –
искомое сечение.
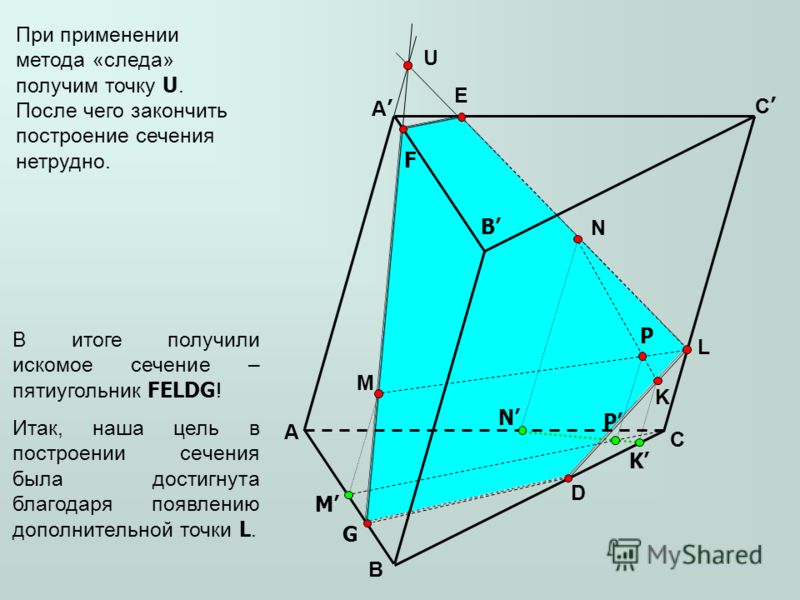
Построить сечение тетраэдра плоскостью,
проходящей через точки E, F, K.
1. Проводим КF.
2. Проводим FE.
3. Продолжим
EF, продолжим AC.
D
F
4. EF AC =М
5. Проводим
MK.
E
M
C 6. MK AB=L
A
7. Проводим EL
L
EFKL – искомое сечение
K
B
Построить сечение тетраэдра плоскостью,
проходящей через точки E, F, K
СКакие
какойпрямые
точкой,
лежащей в
можно
Соедините
получившиеся
Какие
сразу
той
жеточки
граниможно
можно
продолжить,
чтобы
получить
точки,
лежащие
в
одной
соединить?
соединить
полученную
дополнительную
точку?
грани,
назовите
сечение.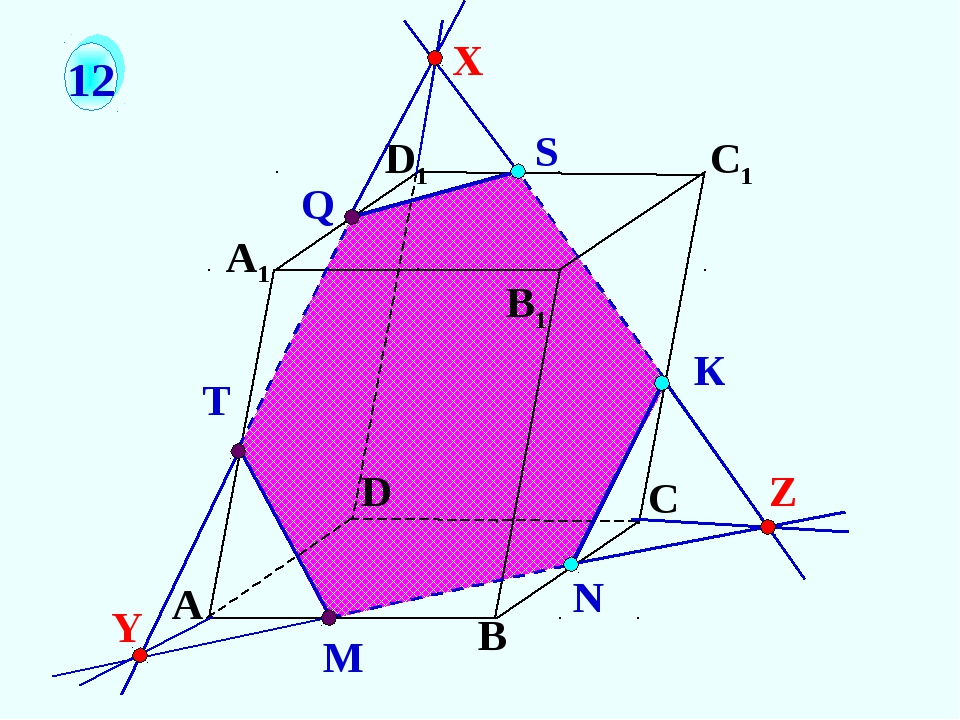
дополнительную точку?
D
иЕ
АС
ЕLFK
FСЕК
иточкой
K,
и FК
F
L
C
M
A
E
K
B
Построить сечение
тетраэдра плоскостью,
проходящей через точки
E, F, K.
D
F
L
C
A
E
K
B
О
Вывод: независимо от способа
построения сечения одинаковые

18. Построение сечений параллелепипеда

Тетраэдр имеет 6 граней
Треугольники
Пятиугольники
В его сечениях могут получиться
Четырехугольники
Шестиугольники

20. Построить сечение параллелепипеда плоскостью проходящей через точку Х параллельно плоскости (ОСВ)

В1
А1
Y
Х
D1
S
В
А
D
Z
1. Проведем через
С1
точку X прямую
параллельную ребру
D1C1
2. Через точку X
прямую
параллельную ребру
D1D
3. Через точку Z прямую
параллельную ребру
С
DC
4. Проведем прямую через
точки S и Y, т.к. они лежат в
одной грани (BB1C1)
XYSZ – искомое сечение
Построить сечение параллелепипеда
плоскостью, проходящей через точки
M,A,D
В1
D1
E
A1
С1
В
А
1. AD
2. MD
3. ME//AD, т.к. (ABC)//(A1B1C1)
4. AE
5. AEMD – искомое сечение
М
D
С

22. Построить сечение параллелепипеда плоскостью, проходящей через точки М, К, Т

N
М
К
R
S
Х
Т

23. Выполните задания самостоятельно

м
т
к
м
Д
к
т
Постройте сечение: а) параллелепипеда;
б) тетраэдра
плоскостью, проходящей через точки М, Т, К.

24. Использованные ресурсы

Соболева Л. И. Построение сечений
Ткачева В. В. Построение сечений
тетраэдра и параллелепипеда
Гобозова Л. В. Задачи на построение
сечений
DVD-диск. Уроки геометрии Кирилла и
Мефодия. 10 класс, 2005
Обучающие и проверочные задания.
Геометрия. 10 класс (Тетрадь)/Алешина
Т.Н. – М.: Интеллект-Центр, 1998

English    
Русский
Правила

სიახლეები — საქართველოს ტექნიკური უნივერს001ტტს001ტტოს

სტუ

მთავარი სიახლეები

სიახლეები

კონკურსები

სიახლეები

სიახლეები

30
მაი

26
მაი

17
მაი

21
აპრ

ყველა მთავარი სიახლე

17
ნოე

ინტერნეტმმართველობის ახალგაზრდული ფორუმი 19-20 ნოემბერს ტექნოპარკში გაიმართება გაიმართება გაიმართება

19-20 ნოემბერს, პირველად საქართველოში საქართველოში ინტერნეტმმართველობის ახალგაზრდული ფორუმი ფორუმი (Форум управления молодежным интернет-управлением) გაიმართება. ღონისძიებას ტექნოპარკი უმასპინძლებს.

17
ნოე

სტუ-ის რექტორი, პროფესორი გურგენიძე, სტუდენტთა საერთაშორისო დღესთან დაკავშირებით, ახალგაზრდებს მიმართავს

16
ნოე

სტუ-ის რექტორი, პროფესორი გურგენიძე, იაპონიაში ვიზიტის ფარგლებში, j-parc- ის შეხვდა შეხვდა შეხვდა შეხვდა შეხვდა შეხვდა შეხვდა შეხვდა შეხვდა შეხვდა

სტუ-ის რექტორი იაპონიაში, მსოფლიოს ერთ-ერთ უდიდეს სამეცნიერო-კვლევით ორგანიზაციებში ორგანიზაციებში ის დირექტორის დირექტორის, პროფესორ მასანორი იამაუჩის მიწვევით მიწვევით იმყოფებოდა.

15
ნოე

საქართველოს ტექნიკური სამძიმარს უცხადებს დაღუპული სტუდენტის, საბა გრიგალაშვილის ოჯახს

15
ნოე

პროფესორ ბორის იმნაძეს 90 წელი შეუსრულდებოდა

ცნობილ პედაგოგს, მეცნიერს, თაობათა აღმზრდელსა და მათთვის ცხოვრების გამკვალავს, ღირსეულ ადამიანს, ჭეშმარიტ ინტელიგენტს — პროფესორ ბორის იმნაძეს დღეს 90 წელი შეუსრულდებოდა.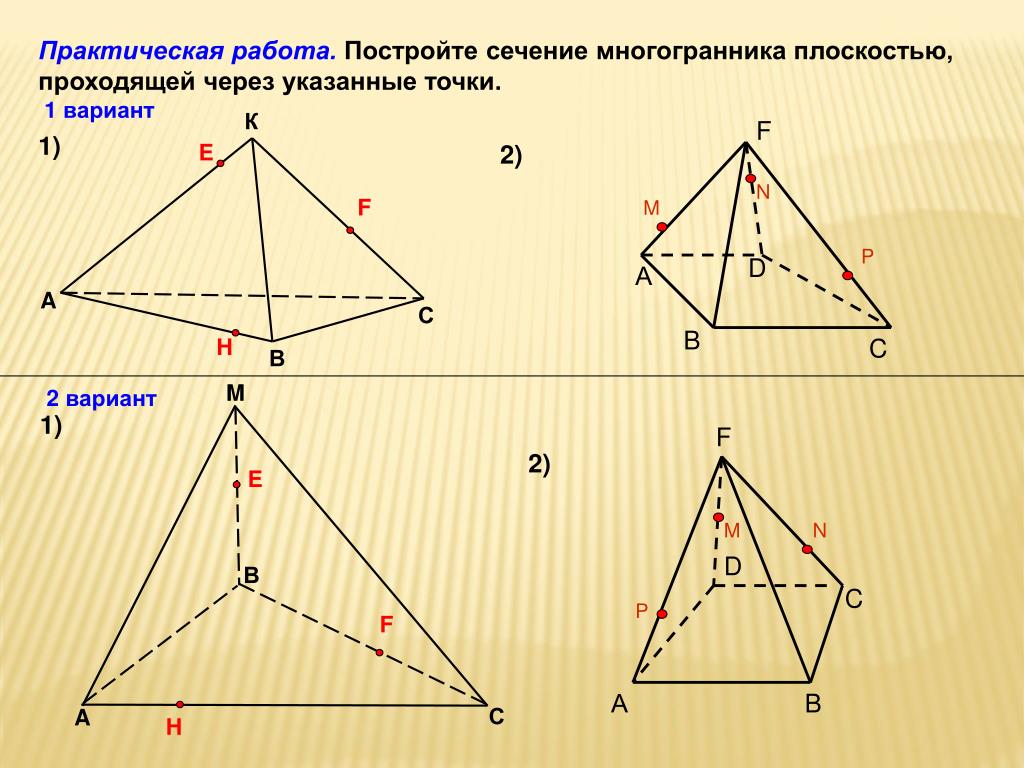

15
ნოე

სტუ-სა „ჯორჯიან მანგანეზს მანგანეზს შორის ურთიერთთანამშრომლობის მემორანდუმი გაფორმდა

საქართველოს უნივერსიტეტის რექტორმა რექტორმა, პროფესორმა დავით და „ჯორჯიან მანგანეზის მანგანეზის« (GM) სპეციალურმა მმართველმა, ნიკოლოზ ჩიქოვანმა და კომპანიას შორის ურთიერთთანამშრომლობის მემორანდუმს მოაწერეს ხელი.

14
ნოე

სტუ-ის რექტორი, პროფესორი გურგენიძე იაპონიაში ვიზიტის ფარგლებში, Kek- ის მენეჯმენტს შეხვდა შეხვდა შეხვდა შეხვდა შეხვდა შეხვდა

საქართველოს უნივერსიტეტის რექტორი, პროფესორი დავით გურგენიძე იაპონიის ქალაქ ცუკუბაში მაღალი ენერგიების ამაჩქარებლის კვლევების ორგანიზაციაში ორგანიზაციაში ის დირექტორის დირექტორის, პროფესორ იამაუჩის ოფიციალური მიწვევით იმყოფებოდა.

14
ნოე

ცნობილი საზოგადო და მეცნიერის, ნოდარ ნათაძის ხსოვნას ხსოვნას ხსოვნას ხსოვნას

ყველა სიახლე

01
ნოე

05
აგვ

03
აგვ

საქართველოს ტექნიკური დაარსებიდან დაარსებიდან 100 წლის იუბილესთან დაკავშირებით აცხადებს საერთაშორისო კონკურსს სივრცულ კონცეპტუალურ კომპოზიციაზე კომპოზიციაზე: „წარსული, აწმყო, მომავალი«

სივრცულ კომპოზიცია განთავსდება თბილისში, კოსტავას, 77-ში, უნივერსიტეტის კორპუსის მიმდებარე ტერიტორიაზე (ს. კ. n 01.10.13.023.181) კონკრეტულ ადგილზე.

20
ივლ

20
ივლ

0322 77 11 11

Нож — Ручной блендер

Ссылка

Режим

Режим редактирования

Инструмент

Панель инструментов ‣ Нож

Ярлык

К

Инструмент «Нож» можно использовать для интерактивного разделения (разрезания)
геометрия путем рисования линий или замкнутых контуров для создания отверстий.

Использование

При использовании Ножа курсор меняется на иконку скальпеля
и заголовок изменится, чтобы отобразить параметры инструмента.
Вы можете нарисовать соединенные прямые линии, нажав ЛКМ ,
отмечены маленькими зелеными квадратиками. Красные квадраты — это уже определенные разрезы.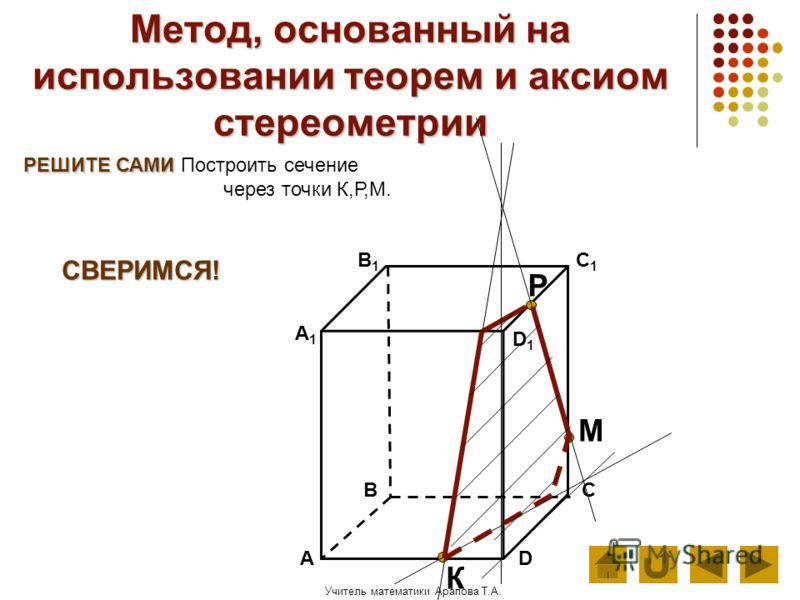
Окружающие красные квадраты означают, что в этом месте уже есть вырез,
поэтому не будет создана дополнительная вершина (кроме первой).

Если перед входом в режим редактирования выбрано несколько объектов,
тогда порезы ножом повлияют на все эти объекты.

Настройки инструмента

Occlude Geometry

На экране видна только вырезанная геометрия.

Only Selected Shift - K

Прорезает только выбранную геометрию.

X-Ray

Также показывать точки среза невидимой геометрии, если параметр Occlude Geometry отключен.

Измерение

Какие видимые измерения отображать.

Расстояние, Угол, Нет, Оба

Угловая привязка

Должны ли перетаскиваемые линии ограничиваться определенными углами, и если да,
к какой системе координат относится угол.

Нет, Экран, Относительный

Приращение угловой привязки

Когда угловая привязка включена, угол будет ограничен кратным этому углу.

Органы управления

Подтвердить Пробел или Возврат

Подтверждает разрез.
Возврат оставит выбранными все ребра, кроме новых ребер, созданных из разреза.

Отмена Esc

Отменяет рез.

Нарисовать непрерывную линию ЛКМ перетащить.

Таким образом, вы можете провести линию от руки по поверхности,
точки будут созданы на пересечениях ребер.

Закрыть петлю двойной щелчок ЛКМ

Это быстрый способ закрыть петлю, которую вы сейчас вырезаете.

Новый разрез юаней

Начинает новый разрез. Это позволяет определить несколько отдельных линий разреза.
Если было определено несколько разрезов, они распознаются как новые точки привязки.

Создание нескольких разрезов.

Результат запуска новых резов в инструменте.

Привязка к средней точке Сдвиг

Удерживайте, чтобы привязать курсор к середине краев,
это означает, что все разрезы будут выполняться точно по центру каждой режущей кромки.

Игнорировать привязку Ctrl

Удерживайте, чтобы инструмент игнорировал привязку,
в отличие от значения по умолчанию, когда курсор мыши привязывается к краям.

Cut Through: C

Разрешить инструменту Cut прорезать закрытые грани, а не только видимые.

Ограничение угла A

Ограничивает линию разреза с шагом в несколько градусов.
Шаг можно указать в настройках инструмента (см. выше) или ввести
когда ограничение угла активно.
Углы по умолчанию в плоскости экрана, но набрав A еще раз
делает его относительно последней режущей кромки.
Если последнее ребро разреза неоднозначно (потому что разрез был на вершине),
ввод R циклически перебирает возможные ребра ссылки.

Ограничение угла среза.

Результат ограничения угла среза.

Ограничение оси X , Y или Z

Ограничивает линию разреза одной из осей системы координат.
Изначально это будет глобальная ось с заданным именем,
но повторное нажатие той же клавиши переключает на локальную систему координат объекта.
Кроме того, если ориентация преобразования сцены установлена ​​на
пользовательской ориентации (например, от лица), ограничения будут в этой системе координат.

Видимые измерения S

Показывает размеры выполняемых разрезов: углы относительно края сетки, длины или и то, и другое.
Повторное нажатие S циклически переключает то, что может быть показано.