Как начертить уклон: Уклон и Конусность • ChertimVam.Ru
Содержание
Уклон и Конусность • ChertimVam.Ru
Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.
Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.
Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.
Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.
Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.
Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.
Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.
Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.
Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.
Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.
Как начертить уклоны и конусность
Во многих деталях машин используются уклоны и конусность. Уклоны встречаются в профилях прокатной стали, в крановых рельсах, в косых шайбах и т. д. Конусности встречаются в центрах бабок токарных и других станков, на концах валов и ряда других деталей.
Уклон характеризует отклонение прямой линии от горизонтального или вертикального направлений. Для того чтобы построить уклон 1:1, на сторонах прямого угла откладывают произвольные, но равные величины (рис. 1). Очевидно, что уклон 1:1 соответствует углу в 45 градусов. Чтобы построить линию с уклоном 1:2, по горизонтали откладывают две единицы, для уклона 1:3 — три единицы и т. д. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а. Величину уклона на чертеже в соответствии с ГОСТ 2.307—68 указывают с помощью линии-выноски, на полке которой наносят знак уклона и его величину. Расположение знака уклона должно соответствовать определяемой линии: одна из прямых знака должна быть горизонтальна, другая — наклонена примерно под углом 30° в ту же сторону, как и сама линия уклона.
д. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а. Величину уклона на чертеже в соответствии с ГОСТ 2.307—68 указывают с помощью линии-выноски, на полке которой наносят знак уклона и его величину. Расположение знака уклона должно соответствовать определяемой линии: одна из прямых знака должна быть горизонтальна, другая — наклонена примерно под углом 30° в ту же сторону, как и сама линия уклона.
На рисунке в качестве примера построен профиль несимметричного двутавра, правая полка которого имеет уклон 1:16. Для ее построения находят точку А с помощью заданных размеров 26 и 10. В стороне строят линию с уклоном 1:16, для чего по вертикали откладывают, например, 5 мм, а по горизонтали 80 мм; проводят гипотенузу, направление которой определяет искомый уклон. С помощью рейсшины и угольника через точку А проводят линию уклона, параллельную гипотенузе.
Конусностью называют отношение диаметра основания конуса к его высоте. В этом случае конусность К=d/l. Для усеченного конуса К = (d-d1)/l. Пусть требуется построить конический конец вала по заданным размерам: d — диаметр вала — 25 мм; I — общая длина конца вала — 60 мм; l1 — длина конической части — 42 мм; d1 — наружный диаметр резьбы — 16 мм; К — конусность 1 : 10 (рис. 3, б). Прежде всего, пользуясь осевой, строят цилиндрическую часть вала, имеющую диаметр 25 мм. Этот размер определяет также большее основание конической части. После этого строят конусность 1:10. Для этого строят конус с основанием, равным 10 мм, и высотой, равной 100 мм (можно было бы воспользоваться и размером 25 мм, но в этом случае высота конуса должна быть взята равной 250 мм, что не совсем удобно). Параллельно линиям найденной конусности проводят образующие конической части вала и ограничивают ее длину размером 42 мм. Как видно, размер меньшего основания конуса получается в результате построения. Этот размер обычно не наносят на чертеж.
В этом случае конусность К=d/l. Для усеченного конуса К = (d-d1)/l. Пусть требуется построить конический конец вала по заданным размерам: d — диаметр вала — 25 мм; I — общая длина конца вала — 60 мм; l1 — длина конической части — 42 мм; d1 — наружный диаметр резьбы — 16 мм; К — конусность 1 : 10 (рис. 3, б). Прежде всего, пользуясь осевой, строят цилиндрическую часть вала, имеющую диаметр 25 мм. Этот размер определяет также большее основание конической части. После этого строят конусность 1:10. Для этого строят конус с основанием, равным 10 мм, и высотой, равной 100 мм (можно было бы воспользоваться и размером 25 мм, но в этом случае высота конуса должна быть взята равной 250 мм, что не совсем удобно). Параллельно линиям найденной конусности проводят образующие конической части вала и ограничивают ее длину размером 42 мм. Как видно, размер меньшего основания конуса получается в результате построения. Этот размер обычно не наносят на чертеж. Запись М16X1,5 является условным обозначением метрической резьбы, о чем подробнее будет сказано дальше.
Запись М16X1,5 является условным обозначением метрической резьбы, о чем подробнее будет сказано дальше.
n
n
TBegin—>TEnd—>
n
n
Рис. 1. Построение уклонов
n
n
Перед размерным числом, характеризующим конусность, наносят условный знак в виде равнобедренного треугольника, вершину которого направляют в сторону вершины самого конуса. Знак конусности располагают параллельно оси конуса над осью или на полке линии-выноски, заканчивающейся стрелкой, как в случае надписи уклона. Конусность выбирают в соответствии с ГОСТ 8593—57 .
n
n
n
n
Рис. 2. Пример построения уклонов
n
n
TBegin—>TEnd—>
n
n
Рис. 3. Построение конусности
n
Конусность 1 3 как начертить
Поверхности многих деталей имеют различные уклоны. Плоские поверхности деталей, расположенные наклонно, на чертежах часто обозначаются величиной уклона. В задании «Проекционное черчение» именно так и задано ребро жесткости или тонкая стенка детали.
В задании «Проекционное черчение» именно так и задано ребро жесткости или тонкая стенка детали.
Уклон характеризует отклонение прямой линии или плоскости от горизонтального или вертикального направления. Для построения уклона 1:1 на сторонах прямого угла откладывают произвольные, но равные единичные отрезки. Очевидно, что уклон 1:1 соответствует углу 45º. Как видно из рис. 34,а, уклон есть отношение катетов: противолежащего к прилежащему, что может быть определено как тангенс угла наклона α прямой. Тогда, чтобы, например, построить уклон 1:7 (рис. 34,б), в направлении уклона откладывают семь отрезков, а в перпендикулярном направлении — один отрезок.
Величину наклона обозначают на чертеже в соответствии с ГОСТ 2.307-68 условным знаком с числовым значением. Уклон указывают с помощью линии-выноски, на полке которой наносят знак уклона и его величину. Расположение знака уклона должно соответствовать определенной линии: одна из прямых знака должна быть горизонтальной, а другая — наклонена примерно под углом 30º в ту же сторону, что и сама линия уклона (рис.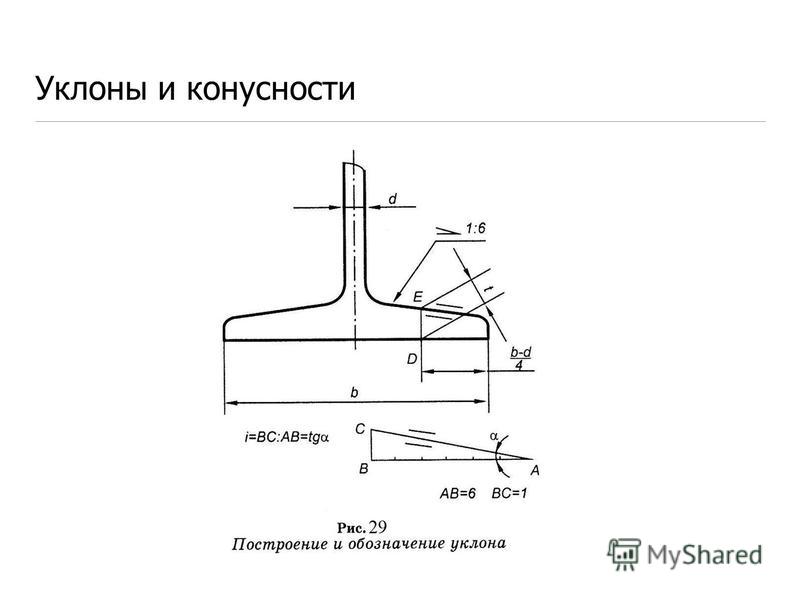 34,б). Вершина знака должна быть направлена в сторону уклона. Знак и размерное число располагают параллельно направлению, по отношению к которому задан уклон. На чертеже уклоны указывают либо в процентах, либо дробью в виде отношения двух чисел.
34,б). Вершина знака должна быть направлена в сторону уклона. Знак и размерное число располагают параллельно направлению, по отношению к которому задан уклон. На чертеже уклоны указывают либо в процентах, либо дробью в виде отношения двух чисел.
| (а) | (б) |
Многие детали содержат коническую поверхность. На чертежах конических деталей размеры могут быть проставлены различно: диаметры большего и меньшего оснований усеченного конуса и его длина, угол конуса или величина конусности.
Конусность — это отношение диаметра основания конуса к его высоте. Для усеченного конуса это отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними (рис. 35,а). Конусность равна удвоенному уклону образующей конуса к его оси. Так же как и уклон, она обозначается условным знаком, проставляемым перед её числовым обозначением. Условный знак изображается в виде треугольника с вершиной, направленной в сторону вершины конуса. Конусность (согласно ГОСТ 2.307-68) задается на чертежах отношением двух чисел (рис. 35), процентами или десятичной дробью.
Конусность (согласно ГОСТ 2.307-68) задается на чертежах отношением двух чисел (рис. 35), процентами или десятичной дробью.
Знак и цифры, указывающие величину конусности, располагают на чертежах параллельно оси конического элемента. Они могут быть расположены над осью, как на рис. 35,б, или полке, как на рис. 35,в. В последнем случае полка соединяется с образующей конуса с помощью линии-выноски, заканчивающейся стрелкой. В конических соединениях, показанных на рис. 36, указание конусности обязательно, так как задание размеров D, d, H из-за трудностей изготовления применяют редко. При построении очертаний конуса, задаваемого конусностью, высотой и одним из диаметров, второй диаметр вычисляют по формуле, приведенной на рис. 35,а. Конусности общего назначения стандартизованы ГОСТ 8593-81.
2. Пример выполнения РГР
На рис. 37 приведен пример варианта задания на выполнение расчетно-графической работы «Проекционное черчение», а также наглядное изображение заданной детали с вырезом.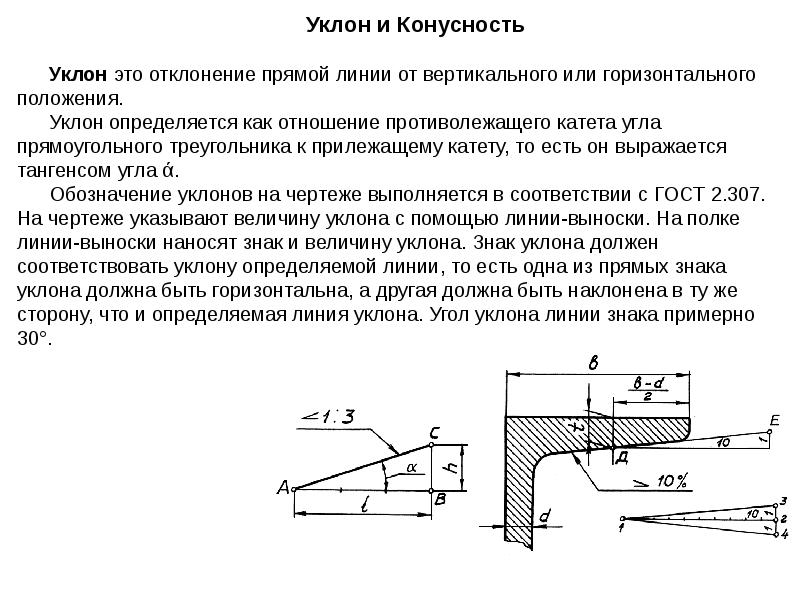
Выполненный по этому заданию чертеж детали в трех проекциях с правильно оформленными размерами показан на рис. 38. Этот пример поможет студентам разобраться в их задании, начать выполнение графической работы и избежать многочисленных ошибок при ее оформлении.
Напомним, что в задании имеются только две проекции детали, поэтому и размеры распределены на двух изображениях. Однако при оформлении чертежа следует наносить размеры равномерно на всех трех проекциях.
В заключение следует отметить, что количество изображений детали (видов, разрезов, сечений) должно быть наименьшим, но обеспечивающим полное представление о её конструкции при применении установленных всоответствующих стандартах условных обозначений, знаков и надписей.
Литература
1. Попова Г.Н., Алексеева С.Ю. Машиностроительное черчение: Справочник. -Л.: Машиностроение, Ленингр. отделение, 1986.
2. Левицкий В.С. Машиностроительное черчение. – М.: Высшая школа, 1988.
3. Гордон В.О., Семенцов-Огиевский Н.А. Курс начертательной геометрии. – М.: Наука, 1994.
4. Фролов С.А. Начертательная геометрия. – М.: Машиностроение, 1978.
Приложение. Варианты задания на расчетно-графическую работу
Варианты задания на расчетно-графическую работу по теме «Проекционное черчение» приведены в табл. П1. Правила выбора варианта задания определяются преподавателем.
Таблица П1. Варианты задания на РГР по теме «Проекционное черчение»
| № вар. | № рис. | а | b | с | № вар. | № рис. | а | b | с |
| П1 | П7 | ||||||||
| П2 | П8 | ||||||||
| П3 | П9 | ||||||||
| П4 | П10 | ||||||||
| П5 | П11 | ||||||||
| П6 | П12 | ||||||||
| П7 | П1 | ||||||||
| П8 | П2 | ||||||||
| П9 | П3 | ||||||||
| П10 | П4 | ||||||||
| П11 | П5 | ||||||||
| П12 | П6 | ||||||||
| П1 | П7 | ||||||||
| П2 | П8 | ||||||||
| П3 | П9 | ||||||||
| П4 | П10 | ||||||||
| П5 | П11 | ||||||||
| П6 | П12 |
[1] Для вертикальных разрезов указанное требование должно выполняться также в случаях, если секущая плоскость не параллельна фронтальной или профильной плоскости проекции
[2] Условие симметричности изображений необходимо, но не достаточно для совмещения половины вида и половины разреза (подробнее см. подраздел 1.2.3).
подраздел 1.2.3).
Дата добавления: 2014-11-06 ; Просмотров: 3188 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Уклоном называют величину, характеризующую наклон одной прямой линии относительно другой прямой. Уклон численно равен тангенсу угла φ
Рис. 4.7. Построение уклона
Уклон может быть задан на чертеже либо отношением двух чисел, либо в процентах. Линию заданного уклона строят как гипотенузу прямоугольного треугольника, тангенс острого угла которого нам известен.
На рис. 4.7, а и б показаны случаи построения прямых, когда уклон их задан отношением двух чисел и в процентах. На рис. 4.7, в показаны варианты практического применения построений линий заданного уклона. Перед числовым значением уклона ставится знак уклона , острый угол которого направлен в сторону уклона.
Конусностью называется отношение диаметра основания конуса к его высоте, либо отношение разности диаметров оснований усечённого конуса к его высоте (рис. 4.8). Как видно из чертежа, числовое значение конусности в два раза больше значения уклона образующей конуса к его оси. На рис. 4.8 показаны примеры построения конусности. Для обозначения конусности на чертеже применяют знак , острый угол которого направлен в сторону конусности. Значение конусности проставляется либо на полке линии выноски, либо над осевой линией.
4.8). Как видно из чертежа, числовое значение конусности в два раза больше значения уклона образующей конуса к его оси. На рис. 4.8 показаны примеры построения конусности. Для обозначения конусности на чертеже применяют знак , острый угол которого направлен в сторону конусности. Значение конусности проставляется либо на полке линии выноски, либо над осевой линией.
Рис.4.8. Построение конусности
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 9825 – | 7406 – или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
1. При помощи ЧП . Повернув головку на заданное число градусов, можно построить любой угол.
2. При помощи транспортира. Приложив центр транспортира к заданной вершине А искомого угла и отметив около шкалы транспортира нулевую точку и точку, соответствующую заданному числу градусов, соединяем обе эти точки с точкой А.
3. При помощи рейсшины и угольников. На Чертеже-№110, а показаны приемы построения углов в 15°, 30°, 45°, 60°, 75° и 90° и дополнительные к ним до 180°.
4. При помощи циркуля и линейки. Таким приемом удобно строить углы, показанные на Чертеже – №110, б.
Деление углов на равные части
Деление произвольного угла пополам. Наиболее удобным приемом деления произвольного угла пополам является деление при помощи циркуля и линейки; последовательность построения биссектрисы угла показана на Чертеже-№111.
Деление прямого угла на три равные части:
1. При помощи ЧП. На Чертеже – №112, а показано, что вдоль кромки линейки, повернутой на 30° . проведен из вершины А луч, а вдоль кромки линейки, повернутой на угол 60° , проведен из вершины А второй луч; получились три угла по 30° .
2. При помощи транспортира. Приложив центр транспортира к вершине А и деление 90° совместив с вертикальной стороной данного прямого угла, намечаем точки против делений в 30° и 60° и соединяем их с вершиной А .
3. При помощи рейсшины и угольника в 30° – 60° – 90° .
На Чертеже – №112, б показано проведение из вершины А луча, наклоненного на угол 60° , и проведение луча, наклоненного на угол 30° .
4. При помощи циркуля и линейки. Построение сводится к проведению двух засечек D и Е и лучей через них из вершины А ; радиус R берется произвольный. Порядок построения показан цифрами в кружках.
Уклоны и конусность
Уклоны. Уклоном прямой по отношению к какой-либо другой прямой называется величина се наклона к этой прямой, выраженная через тангенс угла между ними. Следовательно, уклоном прямой АС относительно прямой АВ называется отношение i = h ÷ l = tg α .
Уклоны обычно выражают отношением двух чисел, например 1 : 6 .
Как видно из чертежа – №113, а, уклон линии выявляется отношением величин двух катетов прямоугольного треугольника ABC , один из которых, например АВ , имеет направление линии, по отношению к которой задан уклон; гипотенузой является отрезок АС прямой заданного уклона. При обозначении уклона перед размерным числом пишут слово «уклон» параллельно линии, по отношению к которой он задан.
При обозначении уклона перед размерным числом пишут слово «уклон» параллельно линии, по отношению к которой он задан.
Взамен слова «уклон» допускается применять знак , вершина угла которого должна быть направлена в сторону уклона (чертеж – №113, в).
Этот знак рекомендуется применять, когда направление уклона неясно выражено.
Проведение через точку А прямой заданного уклона h : l (по отношению к горизонтальной линии). На чертеже – №113, г показаны приемы вспомогательных построений для проведения прямой заданного уклона через заданную точку А : из данной точки А проводят горизонтальный луч и на нем от точки А откладывают длину L (равную числовому значению делителя данного уклона) – получают точку К , через которую проводят вертикальную линию и на ней от точки К откладывают длину h (равную числовому значению делимого данного уклона) – получают точку В . Прямая, проведенная через точки А и В , будет иметь требуемый уклон. Построение можно начинать с проведения вертикального луча из точки А и откладывания на нем величины h .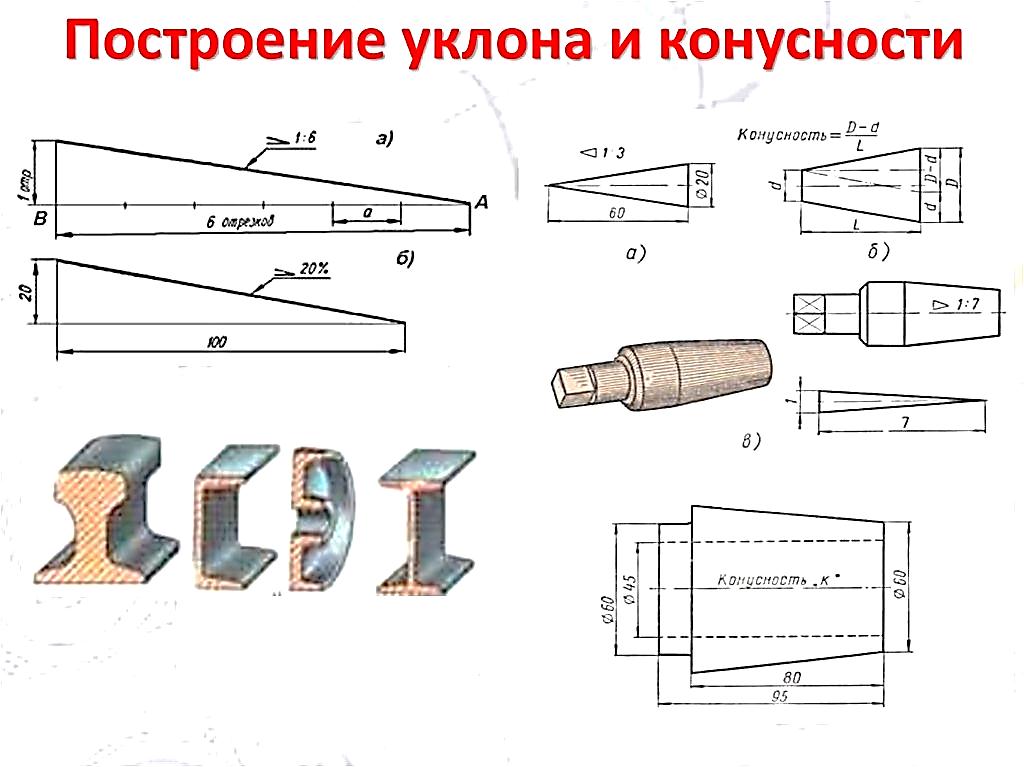
На чертеже – №113, д показан пример применения уклонов на контуре прокатной стали.
УПРАЖНЕНИЕ 3
Начертить контур шаблона с применением построения уклона (чертеж-№113, е).
Конусность. Конусностью называется отношение диаметра D основания конуса к его высоте h . Перед размерным числом конусности следует писать знак >, вершина которого должна быть направлена в сторону вершины конуса (чертеж-№114, а).
Если на чертеже направление конусности выявлено вполне ясно, допускается взамен знака писать слово «конусность» (параллельно оси конуса).
Числовое значение конусности усеченного конуса определяют по формуле (D – d) ÷ L (чертеж-№114, б).
Определение конусности по чертежу и проведение наклонных линий – образующих конуса – согласно данному числовому значению конусности аналогично определению уклонов и проведению прямых заданного уклона.
На чертеже-№114,в показан пример применения построения конусности при изображении детали – пробки.
УПРАЖНЕНИЕ 4
Пример 1. Начертить изображение конической втулки С применением построений, указанных конусностей, согласно чертежу-№114, г.
Начертить изображение конической втулки С применением построений, указанных конусностей, согласно чертежу-№114, г.
Пример 2. Перечертить один из вариантов по заданным размерам с построением указанной конусности (чертеж-№114, д).
Угловые (пропорциональные) масштабы
Угловыми (пропорциональными) масштабами называют графически выраженные числовые масштабы, о которых было сказано (на стр. Масштабы и компоновка чертежей )
Угловые (пропорциональные) масштабы применяют для замены вычислений линейных размеров в том случае, когда чертеж надо выполнить с применением масштаба уменьшения или увеличения. Например, при выполнении чертежа контура пластины в масштабе 1 : 2,5 надо каждую линию предмета изобразить уменьшенной в 2,5 раза. Вычисление уменьшенных размеров каждой линии отнимает много времени. Вместо этого применяют угловой масштаб (чертеж-№115, а), т. е. прямоугольный треугольник (выполненный обычно на миллиметровой бумаге), вертикальный катет ВС которого относится к горизонтальному АС как 1 : 2,5 .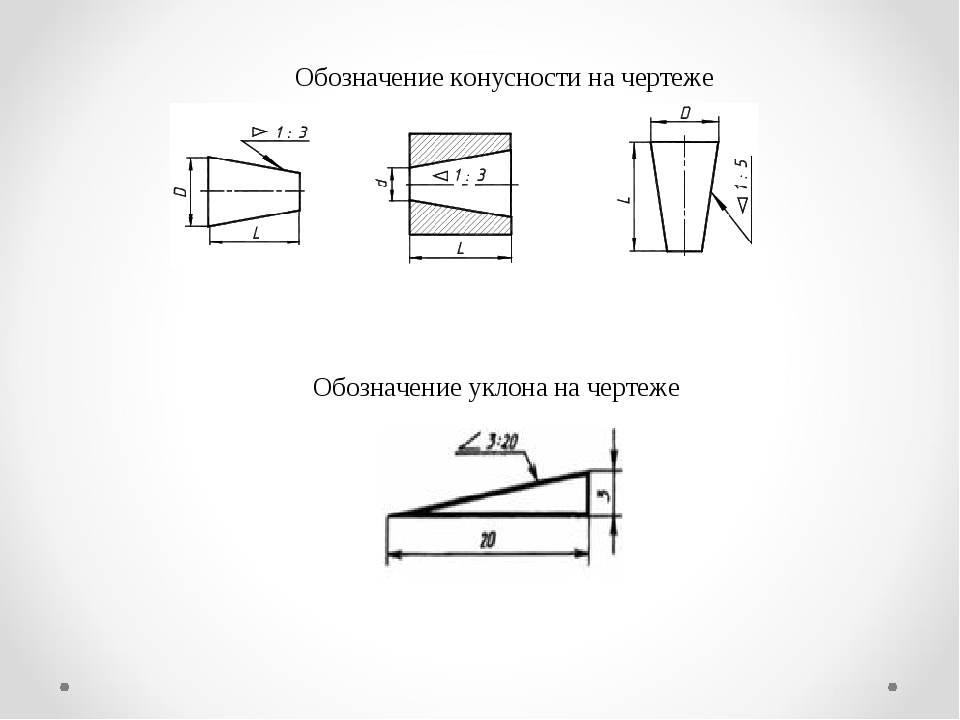
Для уменьшения линий чертежа (чертеж-№115,б) отмеряем разметочным циркулем размер стороны α и, отложив его от вершины А на горизонтальной стороне углового масштаба 1 : 2,5 поворачиваем циркуль вокруг правой иглы и берем по вертикальному направлению до гипотенузы размер α1 , который будет равен α ÷ 2,5
Этот размер переносим на проведенную из заранее намеченной точки К1 вертикальную линию. Из верхней конечной точки проводим вправо горизонтальный луч; на нем откладываем размер стороны b , уменьшенный в 2,5 раза, т. е. b1 (полученный аналогично размеру α1 ; из конечной точки проводим вниз вертикальную линию и на ней откладываем размер с1 и т. д. В результате получим чертеж данной фигуры, выполненный в масштабе 1 : 2,5 .
Чтобы не чертить каждый раз требуемый угловой масштаб, рекомендуется выполнить на миллиметровой бумаге общий угловой масштаб для уменьшений 1 : 2 ; 1 : 2,5 ; 1 : 4 ; 1 : 5 ; 1 : 10 , такой же, какой показан на чертеже-№115, в.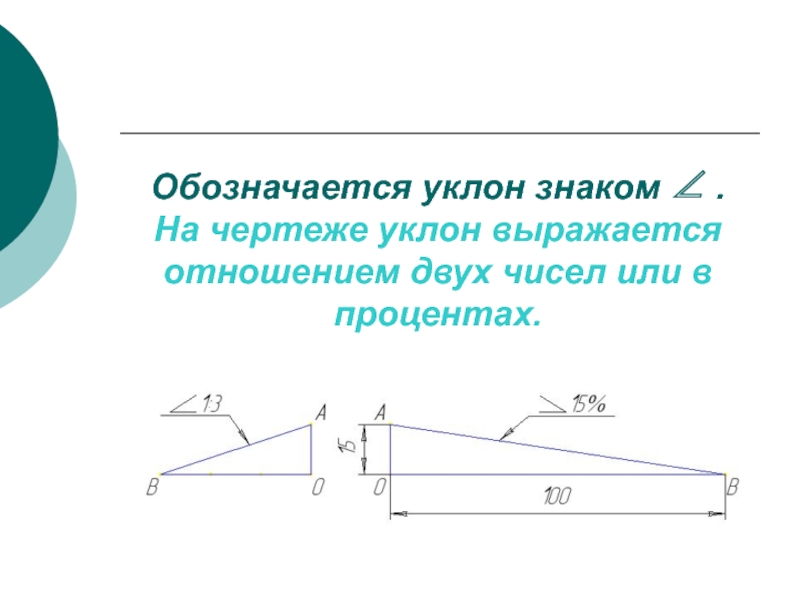
R Калибры для трубной конической резьбы (1/16″ — 6″) ГОСТ 7157-79
В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.
Значение конусности
Рассматривая конусность следует учитывать, что этот показатель напрямую связан с уклоном. Этот параметр определяет отклонение прямой лини от вертикального ил горизонтального положения. При этом конусность 1:3 или конусность 1:16 существенно отличается. Определение уклона характеризуется следующими особенностями:
- Под уклоном подразумевается отношение противолежащего катета прямоугольного треугольника к прилежащему. Этот параметр еще называют тангенс угла.
- Для расчета примеряется следующая формула: i=AC/AB=tga.
Стоит учитывать, что нормальные конусности несколько отличаются от рассматриваемого ранее параметра. Это связано с тем, что конусностью называется соотношение диаметра основания к высоте.
Рассчитать этот показатель можно самым различным образом, наибольшее распространение получила формула K=D/h. В некоторых случаях обозначение проводится в процентах, так как этот переменный показатель применяется для определения всех других параметров.
В некоторых случаях обозначение проводится в процентах, так как этот переменный показатель применяется для определения всех других параметров.
Рассматривая конусность 1:7 и другой показатель следует также учитывать особенности отображения информации на чертеже. Чаще всего подобное отображение проводится при создании технической документации в машиностроительной области.
Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.
Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.
Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.
Черт.1. НАРУЖНЫЕ КОНУСЫ
В настоящее время конуса обычно изготавливают со сменными штревелями, что улучшает совместимость оборудования разных стандартов. Имеет несколько конструктивных разновидностей фланцев, обозначаемых буквами A, B, C, D, E, F.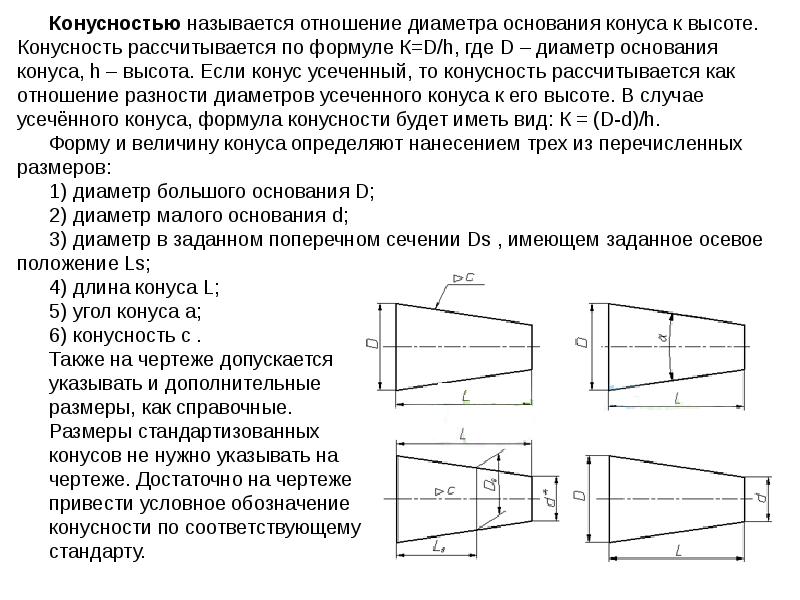 Размер конуса обозначается цифрой наибольшего диаметра фланца в мм (от 25 до 160). Например, HSK-A63.
Размер конуса обозначается цифрой наибольшего диаметра фланца в мм (от 25 до 160). Например, HSK-A63.
Конус Capto, разработанный компанией Sandvik Coromant, сегодня продвигается, как аналог HSK премиум-класса. Однако технология изготовления такого конуса несколько сложнее и следовательно дороже для конечного потребителя. В зависимости от размера соединения Capto обозначаются C3..C10.
Технология нарезания внутренней резьбы
Как уже говорилось выше, перед началом работы надо просверлить отверстие, диаметр которого должен точно подходить под резьбу определенного размера. Следует иметь в виду: если диаметры отверстий, предназначенных под нарезание метрической резьбы, выбраны неверно, это может привести не только к ее некачественному выполнению, но и к поломке метчика.
Учитывая тот факт, что метчик, формируя резьбовые канавки, не только срезает металл, но и продавливает его, диаметр сверла для выполнения резьбы должен быть несколько меньше, чем ее номинальный диаметр.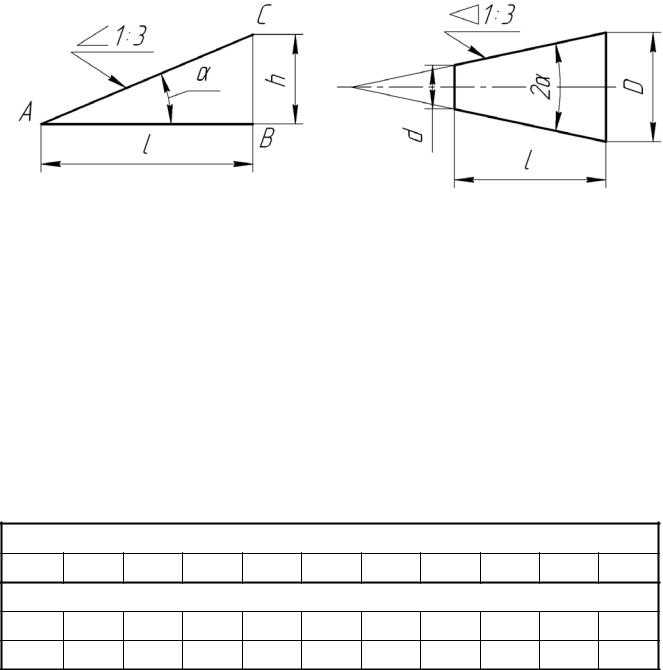 Например, сверло под выполнение резьбы М3 должно иметь диаметр 2,5 мм, под М4 – 3,3 мм, для М5 следует выбирать сверло диаметром 4,2 мм, под резьбу М6 – 5 мм, М8 – 6,7 мм, М10 – 8,5 мм, а для М12 – 10,2.
Например, сверло под выполнение резьбы М3 должно иметь диаметр 2,5 мм, под М4 – 3,3 мм, для М5 следует выбирать сверло диаметром 4,2 мм, под резьбу М6 – 5 мм, М8 – 6,7 мм, М10 – 8,5 мм, а для М12 – 10,2.
Таблица 1. Основные диаметры отверстий под метрическую резьбу
Все диаметры сверл под резьбу ГОСТ приводит в специальных таблицах. В таких таблицах указаны диаметры сверл под выполнение резьбы как со стандартным, так и с уменьшенным шагом, при этом следует иметь в виду, что для этих целей сверлятся отверстия разных диаметров. Кроме того, если резьба нарезается в изделиях из хрупких металлов (таких, например, как чугун), диаметр сверла под резьбу, полученный из таблицы, необходимо уменьшить на одну десятую миллиметра.
Ознакомиться с положениями ГОСТ, регламентирующими нарезание метрической резьбы, можно, скачав документ в формате pdf по ссылке ниже.
Диаметры сверл под метрическую резьбу можно рассчитать самостоятельно. От диаметра резьбы, которую требуется нарезать, необходимо вычесть значение ее шага. Сам шаг резьбы, размер которого используется при выполнении таких вычислений, можно узнать из специальных таблиц соответствия. Для того чтобы определить, какого диаметра отверстие необходимо выполнить с помощью сверла в том случае, если для резьбонарезания будет использоваться трехзаходный метчик, надо воспользоваться следующей формулой:
Сам шаг резьбы, размер которого используется при выполнении таких вычислений, можно узнать из специальных таблиц соответствия. Для того чтобы определить, какого диаметра отверстие необходимо выполнить с помощью сверла в том случае, если для резьбонарезания будет использоваться трехзаходный метчик, надо воспользоваться следующей формулой:
Д о = Д м х 0,8,
где:
Д о
– это диаметр отверстия, которое надо выполнить с помощью сверла,
Д м
– диаметр метчика, которым будет обрабатываться просверленный элемент.
Казалось бы что в трубах сложного? Соединяй и крути… Но, если вы не сантехник и не инженер с профильным образованием, то обязательно возникнут вопросы за ответами на которые придется идти куда глаза глядят. А глядят они скорее всего первым делом в интернет)
Ранее мы уже говорили о диаметрах металлических труб в этом материале . Сегодня же попробуем внести ясность в резьбовые соединения труб различного назначения.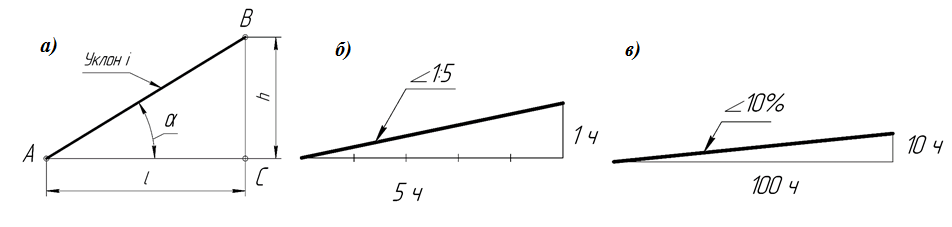 Мы постарались не загромождать статью определениями. Базовую терминологию содержит ГОСТ 11708-82
Мы постарались не загромождать статью определениями. Базовую терминологию содержит ГОСТ 11708-82
с которым каждый может ознакомиться самостоятельно.
Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.
Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.
Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.
Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.
Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.
Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.
Что такое уклон?
Как ранее было отмечено, довольно важным показателем можно считать уклон. Он представлен линией, которая расположена под углом к горизонту. Если рассматривать конусность на чертеже, то она представлена сочетанием двух разнонаправленных уклонов, которые объединены между собой.
Понятие уклона получило весьма широкое распространение. В большинстве случаев для его отображения проводится построение треугольника с определенным углом.
Две вспомогательные стороны применяются для расчета угла, которые и определяет особенности наклона основной поверхности.
Построение уклонов и конусности — Энциклопедия по машиностроению XXL
ПОСТРОЕНИЕ УКЛОНОВ И КОНУСНОСТИ
[c.33]
В первой часта учебника изложены основные правила оформления чертежей в соответствии с Государственными общесоюзными стандартами (ГОСТ), стандартами СЭВ (ОТ СЭВ) даны сведения о различных геометрических построениях построение уклона и конусности, деление отрезков и окружностей на части, построение правильных многоугольников, сопряжение кривых линий отражены вопросы автоматизации расчетно-графических работ и пр. [c.3]
Чертежи необходимо выполнять не только правильно и аккуратно, но и точно.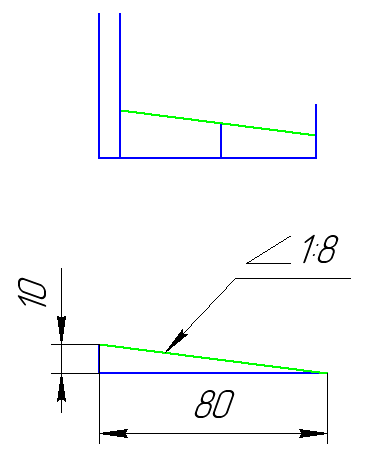 Наиболее элементарными геометрическими построениями на чертежах являются деление отрезков прямой и углов на равные части деление окружности на равные части построение уклонов и конусности. Часто встречаются на чертежах различные виды сопряжений прямых с дугами окружности и дуг окружностей между собой.
[c.35]
Наиболее элементарными геометрическими построениями на чертежах являются деление отрезков прямой и углов на равные части деление окружности на равные части построение уклонов и конусности. Часто встречаются на чертежах различные виды сопряжений прямых с дугами окружности и дуг окружностей между собой.
[c.35]
ПРИЛОЖЕНИЯ ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ I. Деление линии. Построение уклонов и конусностей [c.342]
Построение уклонов и конусности [c.43]
Совершенствование приемов работы чертежными инструментами, выполнение надписей архитектурным и стандартным шрифтами, изучение построений сопряжений, лекальных кривых, построение уклонов и конусностей. [c.12]
Вычертить по заданным размерам контуры стойки и корпуса. Линии построения уклона и конусности [c.35]
Построение уклона и конусности. В очертаниях многих предметов есть прямые, составляющие между собой некоторый угол. На чертежах значение угла между прямыми задают в градусах, уклоном или конусностью (для предметов конической формы).
[c.40]
На чертежах значение угла между прямыми задают в градусах, уклоном или конусностью (для предметов конической формы).
[c.40]
Построение уклона и конусности — см, стр. 72, рис. 23. [c.29]
В книге некоторые темы заданий даны в новом исполнении (шрифты чертежные, построение уклонов и конусности и др.), что позволяет более эффективно их использовать. [c.255]
Глава П1. Построение уклона и конусности [c.6]
ГЛАВА 9 ПОСТРОЕНИЕ УКЛОНА И КОНУСНОСТИ [c.42]
Глава V. Построение и обозначение уклонов и конусности [c.42]
Во втором упражнении предлагается построить контур детали, содержащий примеры на сопряжение линий. Черте жи заданий ко второму упражнению выполнены эскизно, но на них нанесены все необходимые размеры. В ряде случаев учащиеся должны построить уклон и конусность, а также сделать построение в заданном масштабе, отличном от масштаба 1 1.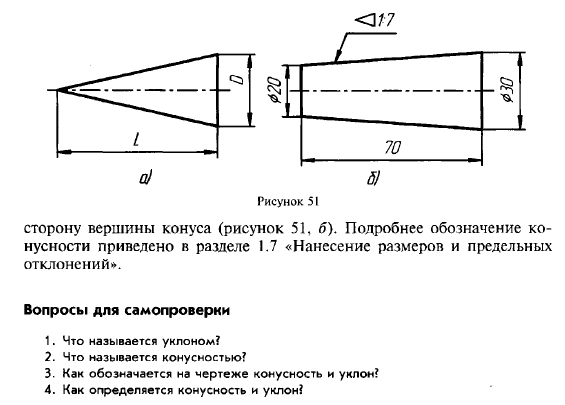 Если масштабы построений для первого и второго упражнений окажутся различными, то их следует подписать над соответствующими построениями, прочеркнув при этом графу Масштаб в рамке основной надписи.
[c.28]
Если масштабы построений для первого и второго упражнений окажутся различными, то их следует подписать над соответствующими построениями, прочеркнув при этом графу Масштаб в рамке основной надписи.
[c.28]
УКЛОН И КОНУСНОСТЬ Уклоном прямой АВ относительно прямой ВС (фиг. 21. б) называется отношение I = = 18 о. Величина уклона может быть выражена простой или десятичной д бью. а также в процентах, Так. например, на фиг. 21, б уклон I = — 1 = 0.75. или =75%. Для построений следует [c.81]
Деление отрезка прямой. Построение и измерение линейных углов. Уклон и конусность. …. [c.373]
Геометрические построения. Деление на равные части отрезков и углов. Уклон и конусность [c.33]
В тех случаях, когда уклон или конусность отчетливо не выявляются, проводят только одну сплошную толстую основную линию (вид сверху на рис. 157, а), соответствующую меньшему размеру элемента с уклоном или меньшему основанию конуса.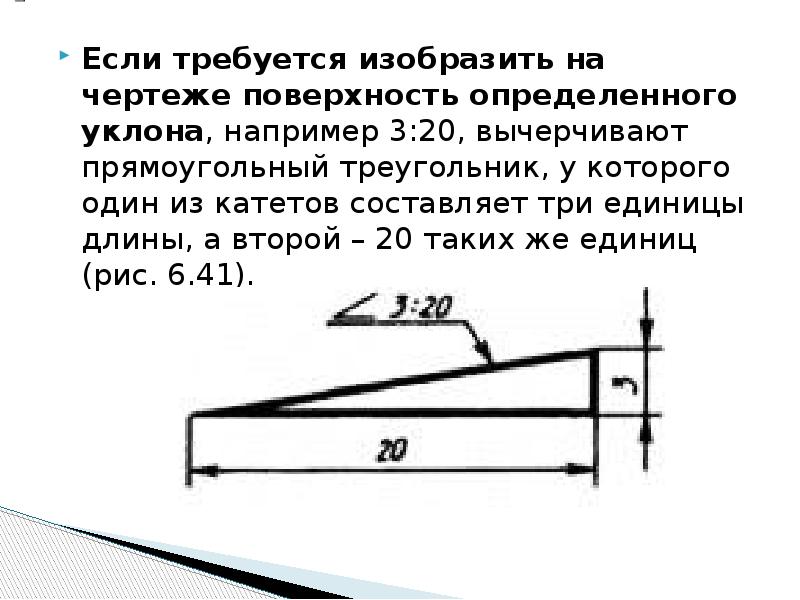 Аналогично оформляют чертеж и в том случае, если при переходе от одной поверхности к другой имеют место скругления (рис. 157,(5). Приведенные на рис. 157 геометрические построения при окончательной обводке чертежа не выполняют.
[c.81]
Аналогично оформляют чертеж и в том случае, если при переходе от одной поверхности к другой имеют место скругления (рис. 157,(5). Приведенные на рис. 157 геометрические построения при окончательной обводке чертежа не выполняют.
[c.81]
При построении очертания конуса, задаваемого конусностью, высотой и одним из диаметров, второй диаметр (на рис. 2.64 равный 30 — 6 — 24 мм) вычисляют по формуле или с помощью вспомогательного треугольника B D, катеты которого относятся как 1 20. Дальше поступают так же, как при построении уклона на рис. 2.58.
[c.46]
Построение уклонов, конусности и углов [c.43]
Таким образом, построение конусности к связано с построением уклона, имеющего угол, тангенс которого равен половине заданной конусности. Например, если к = то = 18 а = и угол а находится построением, как на фиг. 21, б. [c.81]
При построении машиностроительных чертежей деталей часто встречаются уклоны, конусности, фаски.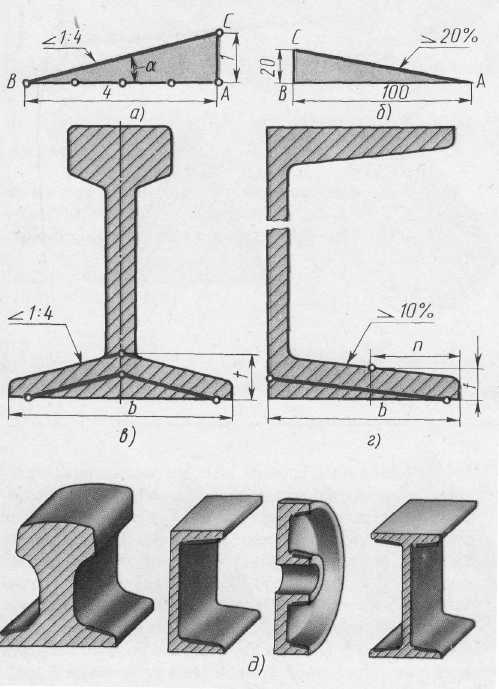 Уклон прямой характеризует е.е наклон к Другой прямой, обычно горизонтальной и реже — вертикальной. Уклон выражает-
[c.51]
Уклон прямой характеризует е.е наклон к Другой прямой, обычно горизонтальной и реже — вертикальной. Уклон выражает-
[c.51]
В машиностроительном черчении часто приходится прибегать к различным геометрическим построениям, в частности строить уклоны, конусности, сопряжения и др. Рассмотрим последовательно, как производят эти построения. [c.36]
Гранка 4. Выполнить чертежи на построение сопряжений (фиг. 13), а также конусности и уклона (табл. 5). [c.12]
При выполнении чертежа калибра и профилей проката (см. табл. 5) нужно начертить изображения конусности и уклона. Для построения задан- [c.20]
Уклоны и конусности. Построения уклонов и конусностей приведено в табл. 1, а их обозначений — на черт. 15, 16, 17. Здесь отметим, что уклоны указываются на чертежах не только в виде соотношения, айв процентах или промиллях (черт. 145). [c.63]
Конусности стандартнзюваны ГОСТ 8593-57. Рассмотрим построение уклонов и конусности на примерах.
[c.36]
Рассмотрим построение уклонов и конусности на примерах.
[c.36]
На рис. 13, в показано построение профиля двутавровой балки (верхней полки, уклон 1 6). Для этого откладывают отточки С enpaiio и влево шесть произвольных, но равных частей и отмечают точки Л. Вниз от точки С откладывают отрезок СВ, равный одной части. Соединив точку А с точкой В, получают прямые, уклон которых равен отношению 1 6. Через заданную точку D Конусность проводят прямую, параллельную АВ. [c.12]
5.3 уклон, конусность, сопряжения
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
Утверждено на заседании кафедры начертательной геометрии и черчения
21 июня 2011г.
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ –
УКЛОНЫ, КОНУСНОСТЬ, СОПРЯЖЕНИЯ
Методические указания для всех специальностей
Квалификация выпуска «Бакалавр»
Ростов-на-Дону
2011
2
Геометрические построения – уклоны, конусность, сопряжения:
Методические указания для всех специальностей.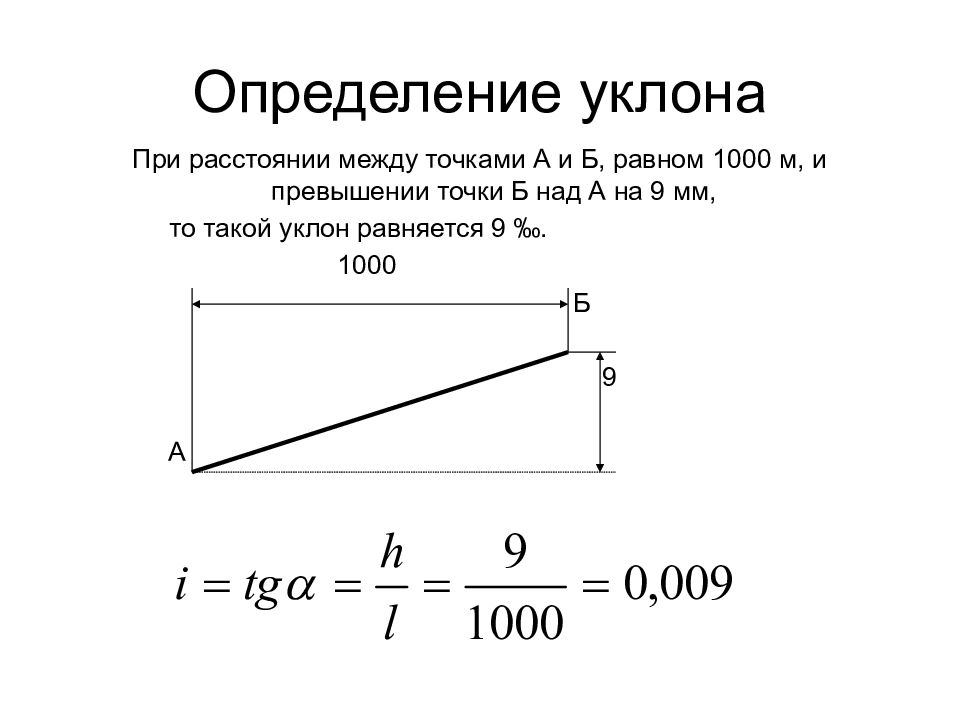 — Ростов н/Д: Рост. гос.
— Ростов н/Д: Рост. гос.
строит. ун-т, 2011. – 8с.
Содержат геометрические построения, необходимые для выполнения задания по инженерной графике.
Составитель: ассист. А.В. Федорова
Редактор Н.Е. Гладких Темплан 2011 г., поз. 137.
____________________________________________________________________
Подписано в печать 6.07.11. Формат 60х84/16.
Бумага писчая. Ризограф. Уч.-изд.л. 0,3. Тираж 20 экз. Заказ 341.
____________________________________________________________________
Редакционно – издательский центр Ростовского государственного строительного университета.
344022, Ростов – на – Дону, ул. Социалистическая, 162
Ростовский государственный строительный университет, 2011
3
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ – УКЛОНЫ, КОНУСНОСТЬ,
СОПРЯЖЕНИЯ
При изготовлении профилей прокатной стали, боковые полки выполняют так, что плоскости, ограничивающие их, не параллельны, а расположены под некоторым углом между собой.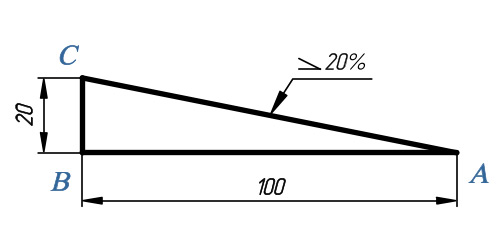
В технике часто применяются конические детали. При вычерчивании чертежей многих деталей приходится выполнять ряд геометрических построений, и в этой связи рассмотрим следующие понятия: уклоны, конусность, сопряжения.
УКЛОНЫ
Уклон – наклон одной прямой линии к другой (рис.1).
Уклон i прямой АС определяется из прямоугольного треугольника АВС как отношение противолежащего катета ВС к прилежащему катету АС (рис.2):
| i | h | BC | tg . |
|
| l | AC |
| ||
|
|
|
| ||
|
|
|
| i | В |
|
|
|
|
| |
1:5 | В |
|
|
| h |
|
|
|
|
| |
А | 1 С |
|
| А | С |
5 4 3 2 |
|
|
| ||
|
|
|
| ||
|
|
|
| l |
|
Рис. |
|
|
| Рис.2 |
|
Уклон может быть выражен в процентах (например, уклон в 10%
внутренних граней полок швеллера по ГОСТ 8240-89, рис. 3), отношением двух чисел (например, уклоны 1:20 и 1:4 граней рельса по ГОСТ 8168-75*) или в промилях (например, уклон 5‰ арматуры).
Знак уклона “ “, вершина которого должна быть направлена в сторону уклона, наносят перед размерным числом, располагаемым непосредственно у изображения поверхности уклона, или на полке линии – выноски, как показано на рисунках.
4
Построение уклонов
1. Провести прямую с уклоном i = 1:6 относительно прямой АЕ через точку А, лежащую на прямой АЕ (рис.3).
1
1:6 В
А 1 2 3 4 5 6 С Е
Отложим на прямой АЕ от точки А шесть произвольно выбранных единиц. Через полученную точку В восстановим перпендикуляр к АЕ длиной в одну единицу.
Рис.3
Гипотенуза АС построенного прямоугольного треугольника АВС
является искомой прямой с уклоном 1:6.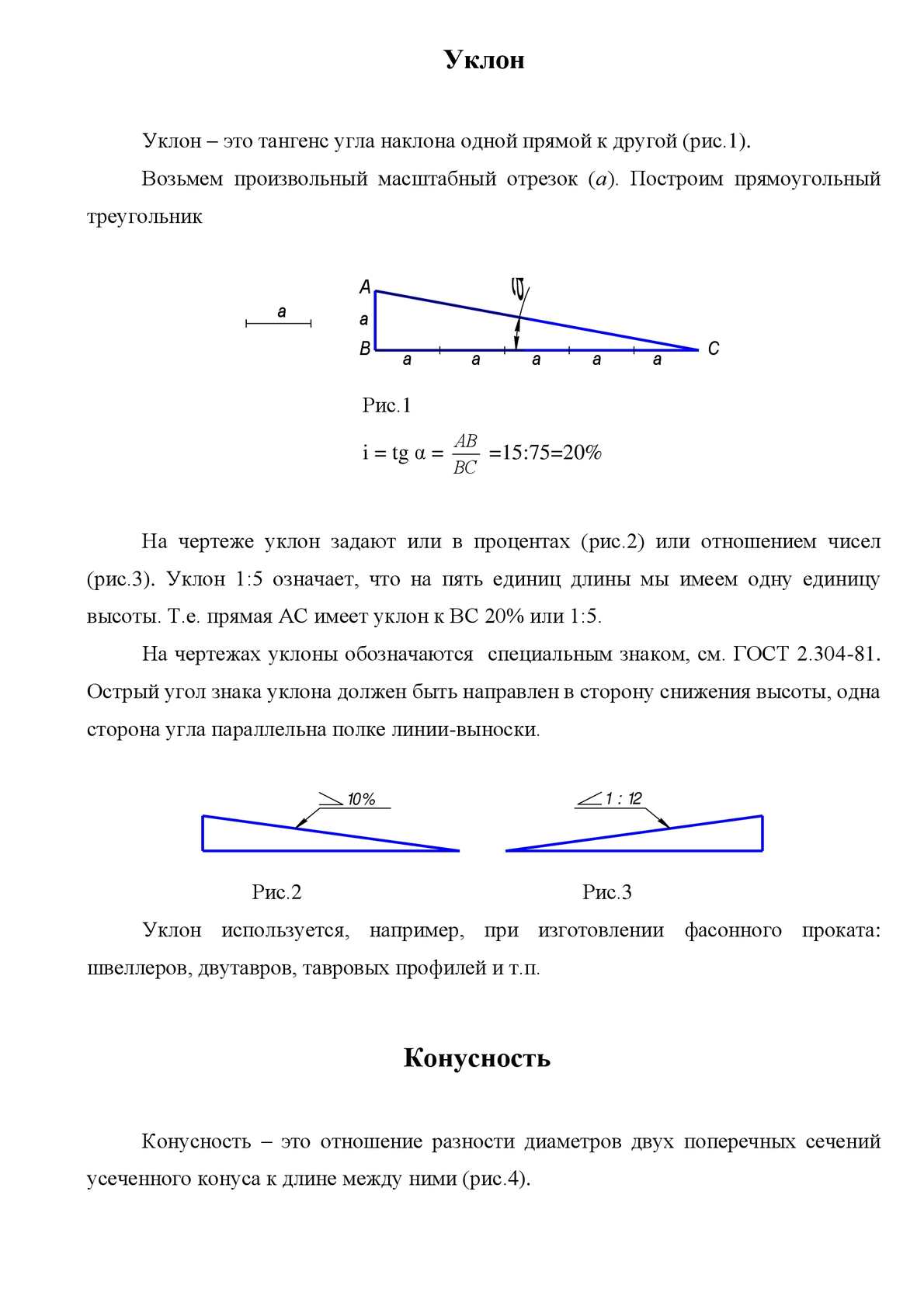
Построение полок швеллера и двутавра
На рис. 4 и 5 показано построение уклона внутренней грани верхней полки швеллера и двутавра. Построен вспомогательный треугольник ВСD с
катетами 10 и 100мм для швеллера и 12 и 100мм для двутавра.
На горизонтальном отрезке «b» отложим отрезок, равный (b-d)/2 – для швеллера и (b-d)/4 – для двутавра. Из полученной точки проведем перпендикуляр длиной t. Отложенные размеры определили положение точки К,
через которую проходит прямая с уклоном 10% для швеллера и 12% — для двутавра. Через точку К провести прямую, параллельную гипотенузе построенного треугольника.
| 10 |
|
|
d |
|
| 100 |
|
|
| |
| R |
| 1:10 |
|
|
| |
|
|
| r |
|
| t | (b-d)/2 |
|
| b |
|
|
|
| Рис. |
| 12 |
|
d |
| 100 |
| R |
|
|
| r |
t |
| (b-d)/4 |
|
| |
|
|
|
|
|
|
b
Рис.5
5
КОНУСНОСТЬ
Конусностью называется отношение диаметра окружности основания D
прямого конуса к его высоте h (рис.6).
КDh .
Для усеченного кругового конуса – отношение разности диаметров двух нормальных сечений конуса к расстоянию между ними (рис.7), т.е.
К | D |
| d | 2tg . |
|
|
| ||
| l |
| ||
|
|
|
|
K
2
Конусность, как и уклон, может быть выражена отношением целых чисел или в процентах. Перед размерным числом, характеризующим конусность,
наносят знак “ ”, острый угол которого должен быть направлен в сторону вершины конуса.
При одном и том же угле конусность в два раза больше уклона, так как уклон образующей конуса равен отношению радиуса его основания к высоте, а
конусность – отношению диаметра к высоте.
Таким образом, построение конусности i : n относительно данной оси сводится к построению уклонов i : 2n с каждой стороны оси.
6
СОПРЯЖЕНИЯ
Сопряжением называется плавный переход по кривой от одной линии,
прямой или кривой, к другой.
Построение сопряжений основано на свойствах прямых, касательных к окружностям, или на свойствах касающихся между собой окружностей.
Построение касательной к окружности
O
При построении прямой, касательной к
Аокружности в заданной точке С, проводят прямую перпендикулярно к радиусу ОС. При
нахождении центра окружности, касающейся заданной прямой в точке С, проводят через эту точку перпендикуляр к прямой и откладывают на нем величину радиуса заданной окружности (рис.8).
Рис.8
Построение внешней касательной к двум окружностям
Из центра О1 проводят вспомогательную окружность радиусом R3 = R1-R2
и находят точку К. Построение точки К аналогично построению точки С. Точку О1 соединяют с точкой К прямой и проводят параллельную ей прямую из точки О2 до пересечения с окружностью. Точки сопряжения С1 и С2 лежат на пересечении прямых О1К и ранее проведенной линии из центра О2 с
окружностями радиусов R1 и R2 (рис. 9).
С2 В
R2
O2
7
Сопряжение двух дуг окружностей
При внешнем касании двух окружностей расстояние между центрами О1
и О2 равно сумме радиусов R1 и R2.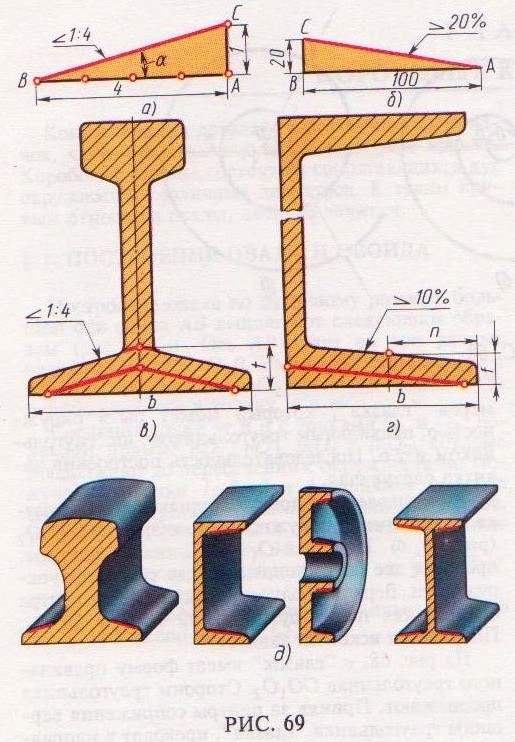 Точка касания С лежит на прямой,
Точка касания С лежит на прямой,
соединяющей центры окружностей (рис.10).
При внутреннем касании окружностей О1О2 = R1 — R2. Точка касания С лежит на продолжении прямой О1О2 (рис.11).
2
R
O1 СO2
С
R1+R2
Рис.10 Рис.11
Сопряжение двух дуг окружностей дугой заданного радиуса
Из центров О1 и О2 описываются дуги вспомогательной окружности радиусом R3 = R + R1 и R4 = R + R2 (при внешнем сопряжении, рис.12)
или R3 = R — R1 и R4 = R — R2 (при внутреннем сопряжении, рис.13). Точка О является центром искомой дуги окружности радиуса R.
Точки сопряжения С1 и С2 будут находиться на линии центров О1О и О2О
(рис.12) или на продолжении линии центров (рис.13).
При нахождении радиуса внешне–внутреннего сопряжения вспомогательные дуги проводятся радиусами R3 = R — R1 из центра О1 и
R4 = R + R2 из центра О2 (рис.14).
Сопряжение окружности с прямой по дуге радиуса R
Из центра О1 проводится дуга радиусом R2 = R1 + R и прямая,
параллельная заданной, на расстоянии R. Пересечение вспомогательной дуги окружности и прямой определит искомый центр О. Точка сопряжения дуг С1
Пересечение вспомогательной дуги окружности и прямой определит искомый центр О. Точка сопряжения дуг С1
лежит на линии центров О1О, а прямой и дуги сопряжения С – на перпендикуляре, проведенном к заданной прямой из центра О (рис.15).
Конусность и уклон — презентация онлайн
1. Конусность и уклон Лекция №4
Предмет «Инженерная графика»
Преподаватель
Пушкарева Роза Васильевна
Во многих деталях машин используются уклоны и
конусность.
Уклоны встречаются в профилях прокатной стали, в
крановых рельсах, в косых шайбах и т. д.
Конусности встречаются в центрах бабок токарных и
других станков, на концах валов и ряда других
деталей.
4. Уклон. Определение уклона
Уклон это отклонение прямой линии от вертикального или
горизонтального положения.
Вершина знака уклона должна быть направлена в сторону наклона
поверхности детали.
Знак и размерное число располагают параллельно направлению, по
отношению к которому задан уклон.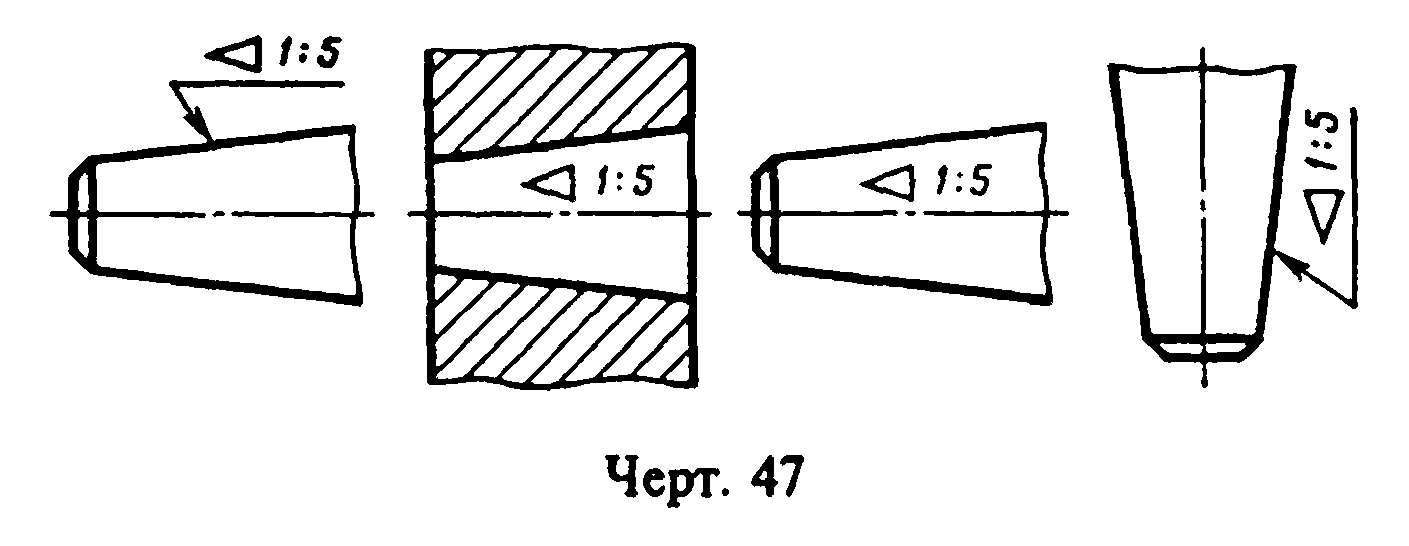
Определение уклона.
Уклон определяется как отношение противолежащего катета угла
прямоугольного треугольника к прилежащему катету, то есть он
выражается тангенсом угла а.
Уклон можно посчитать по формуле i=AC/AB=tga.
Уклоном прямой линии ВС относительно
АВ называется отношение i = h/ι = tgα.
6. Построение уклона.
На примере (рисунок ) наглядно продемонстрировано
построение уклона.
Для построения уклона 1:1, например, нужно на сторонах
прямого угла отложить произвольные, но равные отрезки. Такой
уклон, будет соответствовать углу в 45 градусов.
Для того чтобы построить уклон 1:2, нужно по горизонтали
отложить отрезок равный по значению двум отрезкам
отложенным по вертикали.
Как видно из чертежа, уклон есть отношение катета
противолежащего к катету прилежащему, т. е. он выражается
тангенсом угла а.
7. Построение уклонов.
Если требуется через точку А (рис. 1) прямой АВ
провести прямую АС с уклоном i = 1/n, то надо:
1. Отложить от точки А n произвольных единиц.
Отложить от точки А n произвольных единиц.
2.В конце полученного отрезка АЕ восстановить
перпендикуляр ЕС длиной в одну единицу.
3.Прямая АС — искомая прямая.
Если требуется через точку М, не лежащую на прямой
АВ, провести прямую с заданным уклоном 1:n, то можно
решить задачу двумя способами.
1.Опустить из точки М перпендикуляр МЕ (рис.2) и,
приняв его за единицу, отложить влево и вправо от точки Е
n таких отрезков.
Гипотенузы МД и МД1 — искомые прямые.
2.В стороне строим прямоугольный треугольник
(рис.3) KLN (KLN1) с отношением катетов 1/n.
KL // AB.
Из точки М проводим прямые MD и MD1 параллельно
гипотенузам KN и LN1 вспомогательного треугольника.
9. Обозначение уклона на чертежах.
Обозначение уклонов на чертеже
выполняется в соответствии с ГОСТ 2.307—
2011.
На чертеже указывают величину уклона с
помощью линии-выноски.
На полке линии-выноски наносят знак и
величину уклона.
Знак уклона должен соответствовать
уклону определяемой линии, то есть одна из
прямых знака уклона должна быть
горизонтальна, а другая должна быть
наклонена в ту же сторону, что и
определяемая линия уклона.
Угол уклона линии знака примерно 30°.
Уклон
Плоские
поверхности
деталей,
расположенные
наклонно, обозначают на чертеже величиной уклона.
Как подсчитать эту величину, покажем на примере.
Клин, изображенный на рис. 6.40, имеет наклонную
поверхность, уклон которой нужно определить.
Из размера наибольшей высоты клина вычтем размер
наименьшей высоты: 50 – 40 = 10 мм.
Разность
между
этими
величинами
можно
рассматривать как размер катета прямоугольного
треугольника, образовавшегося после проведения на
чертеже горизонтальной линии (рис. 6.40,б).
Величиной уклона будет отношение размера
меньшего катета к размеру горизонтальной линии.
В данном случае нужно разделить 10 на 100.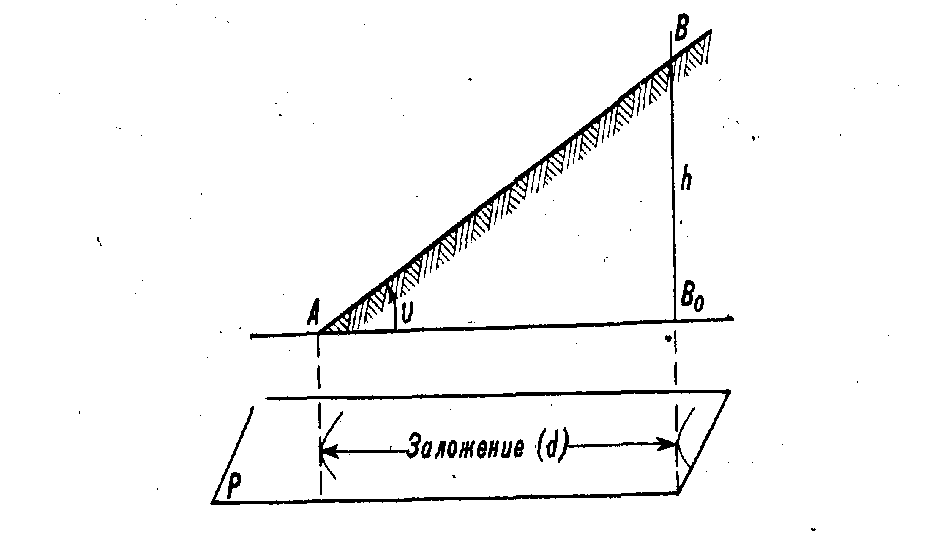
Величина уклона клина будет 1:10.
. Величина уклона клина будет 1:10.
Определение величины уклона
Если требуется изобразить на чертеже
поверхность определенного уклона,
например 3:20, вычерчивают прямоугольный
треугольник, у которого один из катетов
составляет три единицы длины, а второй – 20
таких же единиц (рис. 6.41).
При вычерчивании деталей
или при их разметке для
построения линии по
заданному уклону приходится
проводить вспомогательные
линии.
Например, чтобы провести
линию, уклон которой 1:4,
через концевую точку
вертикальной линии (рис.
6.42), отрезок прямой линии
длиной 10 мм следует принять
за единицу длины и отложить на
продолжении горизонтальной
линии четыре такие единицы
(т.е. 40 мм).
Затем через крайнее деление
и верхнюю точку отрезка
провести прямую линию.
. Построение линии по заданному
уклону
14. Конусность
Конусностью называется отношение разности
диаметров двух нормальных сечений кругового
конуса к расстоянию между ними.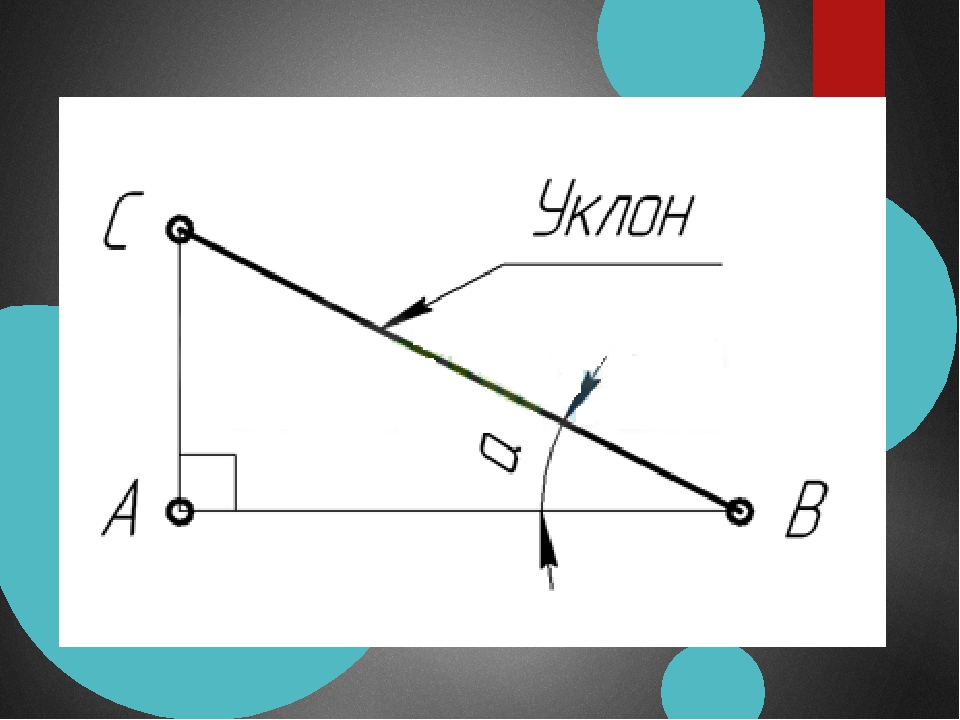
K = (D — d)/ι = 2tgα.
K = 2i.
15. Знак конусности
« »
Конус – лат. conus – геометрическое тело, образованное
вращением прямоугольного треугольника около одного
из его катетов.
На чертежах с коническими поверхностями иногда
указывается конусность c размерными числами в виде
соотношения, перед которыми устанавливается знак в
виде остроугольного треугольника «
».
Знак конусности с размерными числами наносятся
над осевой линией или на полке линии-выноски.
16. Примеры обозначения конусностей
Например, если известны размеры D = 30
мм, d = 20 мм и L = 70 мм, то
К=
30 — 20
70
= 1:7
Если известны конусность К, диаметр одного
из оснований конуса d и длина конуса L, можно
определить второй диаметр конуса.
Например, К = 1:7, d = 20 мм и L = 70 мм
D находят по формуле:
D = КL + d= 1:7 × 70 + 20 = 30 мм
ГОСТ 8593-81 предусматривает следующие
конусности:
1:500, 1:200, 1:100, 1:50, 1:30, 1:20, 1:15, 1:12,
1:10, 1:8, 1:7, 1:6, 1:5, 1:4, 1:3, 30°, 45°, 60°, 75°,
90°, 120°
Конусность
Угловая конусность
Уклон конуса
1:200
0° 17’ 12”
0° 8’ 36”
1:100
0° 34’ 23”
0° 17’ 11”
1:50
1° 8’ 45”
0° 34’ 23”
1:30
1° 54’ 35”
0° 57’ 17”
1:20
2° 51’ 51”
1° 25’ 56”
1:15
3° 49’ 6”
1° 54’ 33”
1:12
4° 46’ 19”
2° 23’ 9”
1:10
5° 43’ 29”
2° 51’ 45”
1:8
7° 9’ 10”
3° 34’ 35”
1:7
8° 10’ 16”
4° 5’ 8”
1:5
11° 25’ 16”
5° 42’ 38”
1:3
18° 55’ 29”
9° 27’ 44”
1:1,866
30°
15°
1:1,207
45°
22° 30’
1:0,866
60°
30°
1:0,652
75°
37° 30’
1:0,500
90°
45°
1:0,289
120°
60°
21.
 ПРАКТИЧЕСКАЯ РАБОТА № 2 Чертеж деталей с применением сопряжений, уклоном и конусностью
ПРАКТИЧЕСКАЯ РАБОТА № 2 Чертеж деталей с применением сопряжений, уклоном и конусностью
Графическую работу следует выполнять на
формате А3 или трех листах А4
Построение линии с учетом точки и наклона
Результаты обучения
- Постройте линию с учетом наклона и точку на линии
В этой главе мы построили линии, нанося точки, используя точки пересечения и распознавая горизонтальные и вертикальные линии.
Другой метод, который мы можем использовать для построения линий, — это метод точки наклона. Иногда нам дается одна точка и наклон линии вместо ее уравнения. Когда это происходит, мы используем определение наклона, чтобы нарисовать график линии.
пример
Изобразите линию, проходящую через точку [latex] \ left (1, -1 \ right) [/ latex], наклон которой равен [latex] m = \ frac {3} {4} [/ latex].
Решение
Постройте заданную точку [latex] \ left (1, -1 \ right) [/ latex].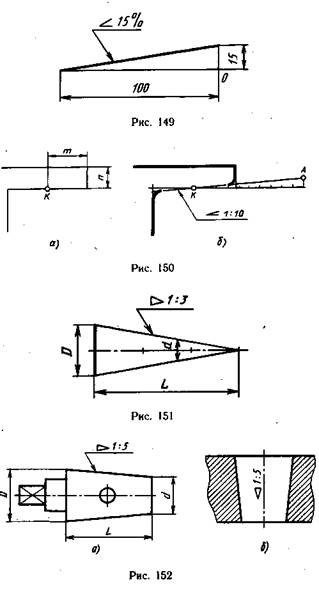
Используйте формулу наклона [latex] m = \ frac {\ text {rise}} {\ text {run}} [/ latex], чтобы определить подъем и спуск.
[латекс] \ begin {array} {} \\ \\ m = \ frac {3} {4} \ hfill \\ \ frac {\ text {rise}} {\ text {run}} = \ frac {3 } {4} \ hfill \\ \\ \\ \ text {rise} = 3 \ hfill \\ \ text {run} = 4 \ hfill \ end {array} [/ latex]
Начиная с точки, которую мы построили, посчитайте Выйдите из подъема и бегите, чтобы отметить вторую точку.Считаем [латекс] 3 [/ latex] единицы вверх и [латекс] 4 [/ latex] единицы справа.
Затем мы соединяем точки линией и рисуем стрелки на концах, чтобы показать продолжение.
Мы можем проверить нашу линию, начав с любой точки и посчитав [латекс] 3 [/ латекс] и вправо [латекс] 4 [/ латекс]. Мы должны добраться до другой точки на линии.
Построение линии с учетом точки и наклона
- Постройте данную точку.
- Используйте формулу наклона для определения подъема и разбега.

- Начиная с данной точки, отсчитайте подъем и бегите, чтобы отметить вторую точку.
- Соедините точки линией.
пример
Изобразите линию с [латексом] y [/ latex] -перерезом [латекс] \ left (0,2 \ right) [/ latex] и наклоном [латекс] m = — \ frac {2} {3} [/ latex ].
Показать решение
Решение
Постройте заданную точку отрезка [latex] y [/ latex] [latex] \ left (0,2 \ right) [/ latex].
Используйте формулу наклона [latex] m = \ frac {\ text {rise}} {\ text {run}} [/ latex], чтобы определить подъем и спуск.
[латекс] \ begin {array} {} \\ \\ m = — \ frac {2} {3} \ hfill \\ \ frac {\ text {rise}} {\ text {run}} = \ frac { -2} {3} \ hfill \\ \\ \\ \ text {rise} = — 2 \ hfill \\ \ text {run} = 3 \ hfill \ end {array} [/ latex]
Начиная с [latex] \ left (0,2 \ right) [/ latex], посчитайте подъем и бег и отметьте вторую точку.
Соедините точки линией.
пример
Изобразите линию, проходящую через точку [latex] \ left (-1, -3 \ right) [/ latex], наклон которой равен [latex] m = 4 [/ latex].
Показать решение
Решение
Постройте данную точку.
| Определите подъем и разбег. | [латекс] m = 4 [/ латекс] |
| Запишите [латекс] 4 [/ латекс] дробью. | [латекс] \ frac {\ text {rise}} {\ text {run}} = \ frac {4} {1} [/ latex] |
| [латекс] \ text {rise} = 4 \ text {run} = 1 [/ latex] |
Подсчитайте подъем и бег.
Отметьте вторую точку. Соедините две точки линией.
Решите наклонные приложения
В начале этого раздела мы сказали, что в реальном мире есть много применений уклона. Давайте теперь посмотрим на несколько.
пример
Уклон крыши здания — это наклон крыши. Знание поля важно в климате с сильным снегопадом. Если крыша слишком плоская, вес снега может вызвать ее обрушение. Какой наклон крыши показан?
Показать решение
Решение
пример
Вы когда-нибудь думали о канализационных трубах, идущих от вашего дома на улицу? Их наклон — важный фактор в том, как они убирают мусор из вашего дома.
Канализационные трубы должны иметь уклон [латекс] \ frac {1} {4} [/ латекс] дюйм на фут для правильного отвода. Какой требуемый уклон?
Показать решение
Решение
| Воспользуйтесь формулой наклона. | [латекс] m = \ frac {\ text {rise}} {\ text {run}} [/ latex] |
[латекс] m = \ frac {- \ frac {1} {4} \ text {in} \ text {.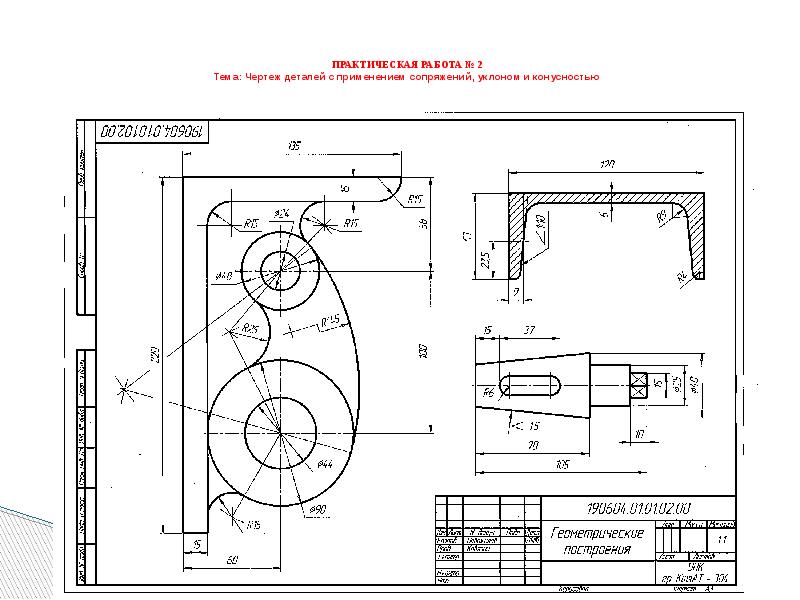 }} {1 \ text {ft}} [/ latex] }} {1 \ text {ft}} [/ latex] | |
| [латекс] m = \ frac {- \ frac {1} {4} \ text {in} \ text {.}} {1 \ text {ft}} [/ latex] | |
| Преобразуйте [латекс] 1 [/ латекс] фут в [латекс] 12 [/ латекс] дюймов. | [латекс] m = \ frac {- \ frac {1} {4} \ text {in} \ text {.}} {12 \ text {in.}} [/ Latex] |
| Упростить. | [латекс] m = — \ frac {1} {48} [/ латекс] |
| Уклон трубы [латекс] — \ frac {1} {48} [/ латекс]. |
Постройте линию, используя наклон и точку пересечения оси Y
Чтобы построить линию, используя ее наклон и точку пересечения y , нам нужно убедиться, что уравнение линии находится в форме пересечения наклона,
Из этого формата мы можем легко считать значения наклона и точки пересечения по оси Y.Наклон — это просто коэффициент переменной x, который равен m, а точка пересечения y — это постоянный член b.
Вот краткая диаграмма, чтобы подчеркнуть эту идею.
Когда эти две части информации идентифицированы, мы гарантированно успешно построим уравнение линии.
Как построить линию с помощью наклона и точки пересечения по оси Y
- Постройте точку пересечения оси y \ left ({0, b} \ right) по оси xy. Помните, что эта точка всегда лежит на вертикальной оси y.
- Начиная с точки пересечения оси Y, найдите другую точку, используя наклон. Наклон содержит направление, в котором вы переходите из одной точки в другую.
Числитель сообщает вам, сколько шагов нужно пройти вверх или вниз (подъем), а знаменатель говорит вам, на сколько единиц нужно переместиться влево или вправо (бег).
- Соедините две точки, образованные пересечением оси Y и наклоном, используя прямую кромку (линейку), чтобы показать график линии.
Примеры построения линии с использованием наклона и точки пересечения по оси Y
Пример 1: Постройте линию ниже, используя ее наклон и точку пересечения по оси Y.
Сравните y = mx + b с заданным уравнением \ large {y = {3 \ over 4} x — 2}. Ясно, что мы можем идентифицировать как наклон, так и точку пересечения по оси y. Y-точка пересечения равна просто b = — 2 или \ left ({0,2} \ right), а наклон равен \ large {m = {3 \ over 4}}.
Поскольку наклон положительный, мы ожидаем, что линия будет увеличиваться, если смотреть слева направо.
- Шаг 1: Давайте построим первую точку, используя информацию, полученную от точки пересечения по оси Y, которая является точкой \ left ({0, — 2} \ right).
- Шаг 2: От точки пересечения по оси Y найдите другую точку, используя наклон. Наклон m = {3 \ over 4}, это означает, что мы поднимаемся на 3 единицы и перемещаемся вправо на 4 единицы.
- Шаг 3: Соедините две точки, чтобы построить линию.
Пример 2: Постройте линию ниже, используя ее наклон и точку пересечения по оси Y.
Я знаю, что наклон равен \ large {m = {{- 5} \ over 3}}, а точка пересечения по оси Y равна b = 3 или \ left ({0,3} \ right). Поскольку наклон отрицательный, окончательный график линии должен уменьшаться, если смотреть слева направо.
- Шаг 1: Начните с построения точки пересечения по оси Y данного уравнения, которая равна \ left ({0,3} \ right).
- Шаг 2: Используйте наклон \ large {m = {{- 5} \ over 3}}, чтобы найти другую точку, используя точку пересечения оси Y в качестве опорной.Наклон говорит нам спуститься на 5 единиц вниз, а затем переместиться на 3 единицы вправо.
- Шаг 3: Проведите линию, проходящую через точки.
Возможно, вас заинтересует:
Три способа построения графика линии
Построение графика линии с использованием таблицы значений
Построение графика линии с использованием точек пересечения по осям X и Y
HartleyMath — Slope Fields
В этом разделе мы увидим первый имеющийся у нас метод анализа дифференциальных уравнений, которые мы не знаем, как решать. Этот метод будет работать для любого дифференциального уравнения первого порядка. Мы начнем с изучения того, как нарисовать картинку, которая представляет все возможные решения уравнения первого порядка, но мы быстро увидим, что, хотя это не так сложно сделать, это может быть очень утомительно, поэтому мы обычно полагаемся на компьютеры. чтобы нарисовать эти графики для нас. Поэтому навык, который нам действительно нужен, — это умение читать эти графики и разбираться в них.
Этот метод будет работать для любого дифференциального уравнения первого порядка. Мы начнем с изучения того, как нарисовать картинку, которая представляет все возможные решения уравнения первого порядка, но мы быстро увидим, что, хотя это не так сложно сделать, это может быть очень утомительно, поэтому мы обычно полагаемся на компьютеры. чтобы нарисовать эти графики для нас. Поэтому навык, который нам действительно нужен, — это умение читать эти графики и разбираться в них.
Проиллюстрируем это на простом примере:
у ‘= т + уу’ = т + уу ‘= т + у
Ясно, что ttt — независимая переменная, а yyy — функция от t.t.t. В нескольких разделах мы узнаем, как решить такое уравнение, но пока мы не можем получить явное решение. Однако, если бы мы знали значение yyy для некоторого значения t, t, t, мы также знали бы значение y′y’y ′ в этой точке. Таким образом, мы можем найти значение y′y’y ′ для каждой возможной комбинации ttt и y.y.y. Каждая комбинация ttt и yyy представляет точку, которую мы можем построить, а y’y’y’ в этой точке — это наклон решения, которое пройдет через эту точку.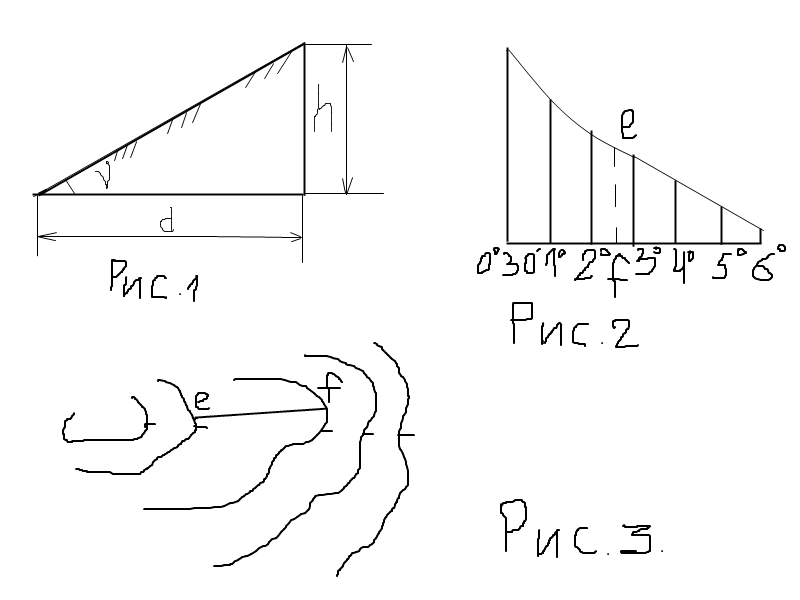
Следовательно, мы можем построить таблицу, подобную приведенной ниже:
tyy ′ = t + y000011101112 ⋮⋮⋮ \ begin {array} {c c c}
т & у & у ‘= т + у \
\ hline
0 & 0 & 0 \
0 и 1 и 1 \
1 & 0 & 1 \
1 и 1 и 2 \
\ vdots & \ vdots & \ vdots
\ end {array} t0011 ⋮ y0101 ⋮ y ′ = t + y0112 ⋮
Чтобы нарисовать поле уклона, мы рисуем короткий отрезок в каждой точке с соответствующим уклоном.Заполненный график выглядит следующим образом:
Что означает поле уклона
?
Самый простой способ прочитать поле уклона — представить его как карту ветров. Если вы уроните лист на эту карту, куда он денется? Это, конечно, зависит от того, куда вы его уроните. Поле наклона представляет все решения дифференциального уравнения (семейство решений, которое мы видели в конце последнего раздела). Конкретное решение зависит от начального состояния, то есть от места, куда падает метафорический лист.
Например, если начальное условие y (0) = 1, y (0) = 1, y (0) = 1, что означает, что y = 1y = 1y = 1, когда x = 0, x = 0, x = 0 решение выглядит так:
Если, с другой стороны, начальное условие y (0) = — 2, y (0) = — 2, y (0) = — 2, решение будет выглядеть так:
Опять же, рисовать поля откосов вручную становится очень утомительно, поэтому вместо этого мы используем компьютеры. Что нам нужно, так это читать поля уклона, поэтому мы попрактикуемся в проведении простых наблюдений.Для этого я буду использовать демонстрацию Wolfram, но она может не работать с вашим браузером (в прошлый раз, когда я проверял, она работала с Firefox). Если вы используете Chrome, вы все равно сможете загрузить проигрыватель Wolfram CDF и загрузить демонстрацию. На всякий случай выложу скриншоты соответствующих частей.
Что нам нужно, так это читать поля уклона, поэтому мы попрактикуемся в проведении простых наблюдений.Для этого я буду использовать демонстрацию Wolfram, но она может не работать с вашим браузером (в прошлый раз, когда я проверял, она работала с Firefox). Если вы используете Chrome, вы все равно сможете загрузить проигрыватель Wolfram CDF и загрузить демонстрацию. На всякий случай выложу скриншоты соответствующих частей.
Демонстрация — Склонные поля из демонстрационного проекта «Вольфрам» Чарльза Э. Олснера. Также существует проект калькулятора Desmos, который может рисовать те же цифры.
Взгляните на следующий пример; мы начнем с этого.
Сделаем два наблюдения из этого поля уклона:
- Наклоны зависят исключительно от yyy (мы также можем определить это, просто взглянув на дифференциальное уравнение). Обратите внимание, что если вы посмотрите вдоль горизонтальной линии (где yyy остается постоянным), все наклоны одинаковы. Это называется автономным дифференциальным уравнением, потому что оно не зависит от независимой переменной.

- Что еще более важно, обратите внимание, что когда y = 1, y = 1, y = 1, все наклоны равны 0.2−1 = 0y2−1 = 0). Но посмотрите на них еще раз; между ними есть четкая разница. Около y = 1, y = 1, y = 1 наклоны отклоняются от положения равновесия, а около y = −1y = −1y = −1 наклоны сходятся к равновесию. Верхнее называется неустойчивым равновесием, а нижнее — устойчивым равновесием. Два классических способа проиллюстрировать разницу показаны на следующих изображениях:
Две диаграммы вверху представляют устойчивое равновесие.Если вы поместите шарик на дно чаши, он останется там, и если вы запустите маятник в вертикальном положении, он также останется там. Это просто то, что значит быть равновесием; система не пытается ничего изменить. Тем не менее, это оба стабильных равновесия, потому что, если вы слегка нарушите систему (немного переместив шарик или слегка толкнув маятник), она вернется в это равновесие.
С другой стороны, рассмотрим две диаграммы внизу; они представляют собой неустойчивое равновесие.
 Если чашу перевернуть вверх дном, дно (теперь верх) все еще будет точкой равновесия, потому что, если вы идеально сбалансируете шарик на вершине, он останется там. Точно так же с маятником, закрепленным внизу, если вы его идеально сбалансируете, он не будет двигаться. Однако в любом из этих случаев, если вы немного нарушите систему, она выйдет из равновесия и никогда не вернется сама по себе.
Если чашу перевернуть вверх дном, дно (теперь верх) все еще будет точкой равновесия, потому что, если вы идеально сбалансируете шарик на вершине, он останется там. Точно так же с маятником, закрепленным внизу, если вы его идеально сбалансируете, он не будет двигаться. Однако в любом из этих случаев, если вы немного нарушите систему, она выйдет из равновесия и никогда не вернется сама по себе.Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}}
{{addToCollection.description.length}} / 500{{l10n_strings.TAGS}}
{{$ item}}{{l10n_strings.
 ПРОДУКТЫ}}
ПРОДУКТЫ}}{{l10n_strings.DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}}
{{$ select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}
{{l10n_strings.
 AUTHOR_TOOLTIP_TEXT}}
AUTHOR_TOOLTIP_TEXT}}{{$ select.selected.display}}
{{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}College Algebra
Урок 27: Графические линииЦели обучения
После прохождения этого руководства вы сможете: - Постройте прямую линию с интервалом y
и наклон. - График вертикальных и горизонтальных линий.

Введение
В этом уроке мы рассмотрим построение линий. Там
Есть несколько способов построения графика линии. Мы будем
глядя конкретно на использование y -intercept
и наклон, чтобы помочь нам получить прямую линию. Я предоставлю обзор
на склоне, а также на форме наклона / пересечения линии, когда мы проходим
этот урок.Если вам нужен более подробный обзор этих концепций, не стесняйтесь.
перейти к Урок 25: Наклон линии и Урок 26: Уравнения линий .
Также будет рассмотрена концепция построения вертикальных и горизонтальных линий.
на этой странице. В основном мы построим пересечение и .
точку, а затем используйте наклон, чтобы найти вторую точку, а затем соедините
точки, чтобы получить график.Учебник
Вот небольшой обзор того, о чем говорит наклон линии
эта линия. Если вам нужно больше отзывов о склоне, не стесняйтесь
Если вам нужно больше отзывов о склоне, не стесняйтесь
перейдите к Урок 25: Наклон линии .Наклон линии измеряет крутизну линии.
Большинство из вас, вероятно, знакомы с ассоциацией наклона с «подъемом».
перебег ».Подъем означает, на сколько единиц вы перемещаетесь вверх или вниз от точки к точке.
точка.На графике это будет изменение на значений y .Бег означает, насколько далеко влево или вправо вы перемещаетесь от точки к точке.
На графике это будет означать изменение на x значение .Вот несколько иллюстраций, которые помогут вам с этим определением:
Положительный наклон:
Обратите внимание, что когда линия имеет положительный наклон, она идет вверх слева направо.

Отрицательный наклон:
Обратите внимание, что когда линия имеет отрицательный наклон, она идет вниз слева направо.
Нулевой наклон:
наклон = 0
Обратите внимание, что, когда линия горизонтальна, наклон равен 0.
Неопределенный уклон:
уклон = undefined
Обратите внимание, что если линия вертикальная, наклон не определен.

Вот небольшой обзор формы наклона / пересечения уравнения
линии. Если вам нужно больше отзывов о склоне, не стесняйтесь
перейдите к Урок 26: Уравнения линий .Уравнение наклона / пересечения прямой Если ваше линейное уравнение записано в такой форме, м представляет наклон, а b представляет собой точку пересечения y .
Эта форма может быть полезна, если вам нужно найти наклон заданной линии.
уравнение.Построение линии с использованием интервала y и
НаклонШаг 1: Положить
уравнение в форме наклона / пересечения ()
и определить наклон и пересечение y .
В такой форме легче определить уклон и
y — перехват линии.В данном виде уклон м , что является
коэффициент перед x и y -перехват
— константа b .Шаг 2: График
пересечение y на двумерном графике.Напомним, что перехват y — это то место, где он
пересекает ось y . Итак, x
значение будет 0.Если вам нужна дополнительная информация о перехватах, см. Учебное пособие по
26: Уравнения линий .
Шаг 3: Использование
наклон, чтобы найти вторую точку на линии.Вы начнете с интервала y и
поднимайтесь вверх или вниз, а затем бегите влево или вправо в зависимости от знака
склон.Используйте понятие уклона как подъема по сравнению с пробегом (подъем / пробег) для определения
как использовать наклон, чтобы найти вторую точку.Какое направление вы считаете положительным?
для подъема, вверх или вниз? Если вы сказали, похлопайте себя
сзади.Это означает, что вниз — это отрицательное направление для подъема.
Чтобы запомнить это, нужно подумать о числах на оси y .
Положительные значения поднимаются вверх над началом координат, а вниз — вниз.
происхождение — отрицательные значения.Какое направление вы считаете положительным?
для бега вправо или влево? Если ты правильно сказал, погладь себя
сзади. Это означает, что влево — это отрицательное направление для бега.
Чтобы запомнить это, представьте себе числа на оси x . Справа от начала координат находятся
положительные значения, а слева от начала координат — отрицательные значения.Если наклон положительный , то
подъем и бег должны быть либо положительными, либо отрицательными.
Другими словами, вы будете вверх и вправо ИЛИ вниз и до
левый .Причина, по которой работают оба отрицательных направления, — это наш уклон.
повышается за пробег, и если у вас есть отрицательный результат над отрицательным, это упрощает
быть положительным.
Если наклон отрицательный , то
подъем и бег должны быть противоположны друг другу, нужно быть положительным
и нужно быть отрицательным. Другими словами, вы пойдете
вверх и влево ИЛИ вниз и вправо . Если вы сделаете их
оба отрицательные, тогда было бы проще быть положительным, и у вас было бы
неправильный график, и вы не хотите этого делать.Также имейте в виду, если ваш наклон является ненулевым целым числом, например -5 или 10,
что есть знаменатель или пробег вашего склона. Что
знаменатель ненулевого целого числа? Если вы сказали
1, вы правы !!!Шаг 4: Рисование
линия, проходящая через точки, найденные на шагах 2 и 3.Все графики в этом руководстве будут прямыми линиями.

Это уравнение уже имеет форму наклона / пересечения:
* Форма уклона / пересечения
Сопоставляя форму с приведенным нам уравнением, видите ли,
что такое наклон и пересечение y- ?В данном виде уклон составляет м , что
— это число перед x .В нашей проблеме
что должно быть 3.В этой форме интервал y равен b ,
что является константой. В нашей задаче это будет 1 .Как поживаете?
Поскольку интервал y — это место, где линия
пересекает ось y , затем x
значение должно быть 0. На шаге 1 мы нашли наш перехват y
На шаге 1 мы нашли наш перехват y
значение равно 1.Собирая все вместе, заказанная пара для y -intercept
будет (0, 1):На шаге 1 мы обнаружили, что наклон равен 3. Что бы знаменатель
из 3 быть? Если вы сказали 1, вы правы.Итак, мы можем думать о
3 как 3/1. Это упрощает представление об этом как о подъеме за бегом (подъем / бег).Поскольку у нас положительный наклон, подъем и разбег должны быть
быть ОБОИМ положительным или ОБОИМ отрицательным. Итак, мы можем подняться на 3 и
бегите вправо 1 ИЛИ спускайтесь на 3 и влево 1.Я выбрал , поднимитесь на 3 и бегите вправо 1, начиная с y -intercept ::
Обратите внимание, что если бы мы пошли вниз на 3 и оставили 1 из нашего интервала y ,
что мы оказались бы в (-1, -2), что совпало бы с
другие моменты.Решите для y , чтобы получить его в уклоне / пересечении
форма:* Инверсия доп. 3 x — под.3 x
* Инверсная по отношению к мульт. 2 — это div. 2
* Форма откоса / пересечения
Сопоставив форму с полученным уравнением, вы можете увидеть, какой наклон
а у- перехват есть?В данном виде уклон составляет м , что
— это число перед x .В нашей проблеме
что должно быть -3/2.В этой форме интервал y равен b ,
что является константой. В нашей задаче это будет 3 .Как поживаете?
Поскольку интервал y — это место, где линия
пересекает ось y , затем x
значение должно быть 0.На шаге 1 мы нашли наш перехват y
значение должно быть 3.Собирая все вместе, заказанная пара для y -intercept
будет (0, 3):На шаге 1 мы обнаружили, что наклон равен -3/2.
Поскольку у нас отрицательный наклон, подъем и спуск должны быть противоположными
друг друга, одно должно быть положительным, а второе — отрицательным.
Итак, мы можем либо спуститься на 3 и бежать вправо 2, либо подняться на 3 и бежать влево 2.Я выбрал , спуститься на 3 и бежать вправо 2, начиная с интервала и :
Обратите внимание, что если мы поднялись на 3 и побежали влево на 2 от нашего интервала y ,
мы бы оказались на (-2, 6), что совпало бы с другими
точки.Это уравнение уже имеет форму наклона / пересечения:
* Форма уклона / пересечения
Сопоставляя форму с приведенным нам уравнением, видите ли,
что такое наклон и пересечение y- ?В данном виде уклон составляет м , что
— это число перед x .В нашей проблеме
что должно быть 5/2.В этой форме интервал y равен b ,
что является константой. В нашей задаче это будет 0 .Как поживаете?
Поскольку интервал y — это место, где линия
пересекает ось y , затем x
значение должно быть 0.На шаге 1 мы нашли наш перехват y
значение должно быть 0.Собирая все вместе, заказанная пара для y -intercept
будет (0, 0):На шаге 1 мы обнаружили, что наклон равен 5/2.
Поскольку у нас положительный наклон, подъем и спуск должны быть
ОБЕ положительные или ОБЕ отрицательные.Итак, мы можем подняться на 5 и бежать
вправо 2 ИЛИ вниз 5 и влево 2.Я выбрал , подняться на 5 и бежать вправо 2, начиная с пересечения и :
Обратите внимание, что если бы мы пошли вниз на 5 и оставили 2 от нашего интервала y ,
мы бы оказались на (-2, -5), что совпало бы с другими
точки.Если у вас есть уравнение x = c ,
где c — константа, и вы хотите
чтобы изобразить это на двухмерном графике, это будет вертикальная линия с пересечением x
из ( c , 0).Даже если вы не видите в уравнении y ,
вы все еще можете изобразить его на двухмерном графике. Помни это
график — это совокупность всех решений данного уравнения. Я упал
точки являются решениями, тогда любая упорядоченная пара, имеющая значение x , равное c , будет решением. Пока
поскольку x никогда не меняет значение, это
всегда c , тогда у вас есть решение.В
в этом случае вы получите вертикальную линию.Ниже представлена вертикальная линия x = c :
Как упоминалось выше, наклон вертикальной линии
не определено .Также обратите внимание, что кроме вертикальной линии x = 0, вертикальная
линия не проходит через ось y .
Это означает, что вертикальная линия не имеет пересечения y ,
если только это не x = 0.Если у вас есть уравнение y = c ,
где c — константа, и вы хотите
чтобы изобразить это на двухмерном графике, это будет горизонтальная линия
с y — перехват (0, c ).Даже если вы не видите x в уравнении,
вы все еще можете изобразить его на двухмерном графике. Помни это
график — это совокупность всех решений данного уравнения. Я упал
точки являются решениями, тогда любая упорядоченная пара, имеющая значение y , равное c , будет решением. Пока
поскольку y никогда не меняет значение, это всегда c, тогда у вас есть решение.
В этом случае вы получите горизонтальную линию.Ниже представлена горизонтальная линия y = c :
Как упоминалось выше, горизонтальная линия имеет
уклон 0 .Пересечение y горизонтальной линии равно любому значению y .
Обратите внимание на то, как у нас есть уравнение, в котором y установлено равным константе, а не x .
Поскольку этот соответствует форме y = c , описанной выше , мы можем сократить до
погоня и рисуем нашу горизонтальную линию:Если у нас горизонтальная линия, каков будет угол наклона?
Если вы сказали 0, вы так правы !!!Что будет с перехватом y ? Дайте
Дайте себе пять, если вы сказали 2.Обратите внимание, как нам не хватает y и хотя
это не совсем в виде x = c ,
что мы можем получить это в такой форме.Давайте сначала перепишем это в виде x = c , а затем перейдем оттуда:
* Записывается в форме x = c
Обратите внимание, что у нас есть уравнение, в котором x установлено равным константе, а не y .
Поскольку этот соответствует форме x = c , описанной выше , мы можем перейти к
погоня и рисуют нашу вертикальную линию:Поскольку у нас есть вертикальная линия, каков будет угол наклона?
Если вы сказали undefined, то вы правы !!!Что будет с перехватом y ? Дайте
Дайте себе пять, если вы сказали, что нет y -перехват.Практические задачи
Это практические задачи, которые помогут вам перейти на следующий уровень.
Это позволит вам проверить и понять, понимаете ли вы эти
типы проблем. Математика работает как и все
в противном случае, если вы хотите добиться успеха в этом, вам нужно практиковать это.
Даже лучшие спортсмены и музыканты получали помощь и много
практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте.
На самом деле не бывает слишком много практики.Чтобы получить максимальную отдачу от них, вы должны решить проблему на
свой, а затем проверьте свой ответ, щелкнув ссылку для ответа / обсуждения
для этой проблемы . По ссылке вы найдете ответ
а также любые шаги, которые позволили найти этот ответ.Практика
Задачи 1a — 1d: Задать наклон и y — пересечение
заданной линии , а затем изобразите ее.Нужна дополнительная помощь по этим темам?
Последний раз редактировал Ким Сьюард 11 февраля 2010 г.
Авторские права на все содержание (C) 2002 — 2010, WTAMU и Kim Seward. Все права защищены.Обозначения склонов и участки откосов
Вы можете использовать наш инструмент Выноски откосов , чтобы разместить выноски, которые показывают направление и процент или соотношение уклонов на чертеже.Вы также можете использовать этот инструмент вместе с нашим инструментом Отметка точки , чтобы обозначить уклон между двумя существующими отметками.
Кроме того, мы встроили в этот инструмент функцию Slope Area . С помощью «Области уклона» вы можете применить определенный уклон к замкнутым областям полилинии на чертеже. Любые интеллектуальные объекты (например, растения, RefNotes или ирригационное оборудование), представленные штриховками, которые находятся в пределах участков откоса, будут пересчитаны для отражения уклона.
Обозначения откосов связаны с высотными отметками. Для получения дополнительной информации см. Нашу страницу документации Spot Elevation .
Обзор условных обозначений уклона
Откройте инструмент Выноска откоса :
F / X Site лента, обозначение уклона и выпадающее меню
Размер сайта панель инструментов
F / X Site menu, Slope Callout and Area option
или введите FX_PlaceSlopeCallout в командной строке
Курсор превратится в коробку для выбора.В командной строке появится запрос: стрелка или выберите размер откоса или отметку первой точки.
На данный момент у вас есть несколько вариантов:
Поместите стрелку вручную
Чтобы разместить стрелку вручную, просто щелкните, чтобы разместить стрелку выноски. Затем вы можете использовать мышь, чтобы сориентировать выноску, а затем введите процент уклона в диалоговом окне Уклон .
Выберите положение стрелки, затем отрегулируйте ориентацию обозначения уклона.
Введите процент уклона в диалоговом окне.
Будет размещена выноска откоса.
Выберите размерную линию уклона
Курсор превратится в поле выбора, когда вы откроете инструмент Выноска откоса . Используйте поле выбора, чтобы выбрать одну из размерных линий уклона, которые появляются при размещении отметок в точках относительно друг друга.
Используйте переключатель, чтобы выбрать «размерную линию» отметки.
Обозначение этого уклона появится вдоль линии.
Поскольку размерная линия не является графиком, она не будет отображаться при печати.
Выберите два обозначения отметки точки
Вы также можете выбрать два обозначения отметки точки. Обозначение уклона появится между двумя обозначениями отметки точки с указанием процента уклона для этих отметок.
Используйте поле выбора, чтобы выбрать текстовую часть первой выноски отметки точки.Затем выберите текстовую часть второй выноски отметки точки.
Обозначение уклона будет помещено между ними.
Выбирая две выноски отметки точки, убедитесь, что вы выбрали текстовые части выноски. В противном случае выноска отметки откоса будет пустой.
При вычислении уклона обратите внимание, что если вы выберете обозначение отметки точки, в котором перечислены несколько отметок, система будет использовать для расчета отметку Точка 1 .
Склоны
Область уклона берет процент уклона или соотношение существующего обозначения уклона и применяет его к замкнутой области полилинии на чертеже. Объекты, представленные любой интеллектуальной штриховкой внутри этой полилинии, будут иметь пересчет количества, объема или площади в зависимости от уклона.
Вы можете нарисовать области откоса на лету или выбрать границу существующей интеллектуальной штриховки, чтобы преобразовать ее в область откоса. Эту функцию можно применить к интеллектуальной штриховке, представляющей такие объекты, как:
- Почвопокровные и кустарниковые зоны
- Справочные примечания по площади или объему (ссылочные примечания)
- Площади капельного орошения
Как работают склоны:
Уклон региона напрямую влияет на количество фактической площади, покрытой этим регионом.Например, если у вас есть две области — одна наклонная и одна плоская — которые выглядят одинаковыми по размеру и форме на виде сверху, наклонная область всегда будет больше. Когда вы создаете область уклона, все умные штриховки (не блоки) в ней будут пересчитаны с учетом увеличения квадратных футов или метров в результате процента или соотношения уклона в этой области, что обычно приводит к увеличению количества или величины. В случае участков капельного трубопровода поток также будет регулироваться в соответствии с увеличением капельного трубопровода и эмиттеров.
Обратите внимание, что участки откоса не повлияют на участки капельного излучателя, длину труб или что-либо, представленное блоками, например отдельные деревья или кустарники, удобства участка или компоненты орошения, за исключением участков капельного трубопровода.
Чтобы создать область уклона, откройте инструмент Выноска откоса . Курсор превратится в коробку для выбора. Используйте это поле выбора, чтобы выбрать существующее обозначение откоса, которое вы хотите использовать при создании области. Процент или соотношение, выраженное этим условным обозначением, будет применяться ко всей площади уклона.
В этом примере мы выберем существующее обозначение уклона, показывающее процент уклона 38,9%.
После выбора выноски в командной строке вам будет предложено выбрать полилинию или [ D raw]:
Вы можете выбрать существующую область полилинии на чертеже, чтобы преобразовать ее в область уклона, или нажать D, чтобы нарисовать область уклона на лету. В нашем примере мы введем D, а затем нарисуем замкнутую область полилинии, которая станет нашей областью уклона.
После того, как вы выбрали или нарисовали замкнутую полилинию, она преобразуется в область уклона и будет содержать обозначение области уклона, указывающее уклон, который теперь применяется ко всей области. Выноска будет имитировать направление уклона выбранной выноски уклона, но при этом будет отображаться тот же уклон и будет вставлена в геометрический центр области уклона.
В нашем примере модель 38.Наклон 9%, выраженный выбранным нами обозначением уклона, теперь будет применяться ко всей области уклона. Например, растения в люке почвопокровного покрова в данной области теперь будут пересчитываться на основе этого уклона, когда мы маркируем эти растения или размещаем расписание растений.
Обратите внимание, что условные обозначения области уклона по умолчанию не будут отображены, то есть они не будут отображаться при печати чертежа. Если вы хотите видеть эти выноски на своем чертеже, вы можете выбрать их и либо изменить их слои для печати, либо переместить их в слои, для которых настроена печать.
Как участки откоса взаимодействуют с другими инструментами Land F / X и AutoCAD
Мы интегрировали Slope Areas в ряд других инструментов Land F / X следующими способами:
- Выделить завод и Выделить объект : эти инструменты будут выделять только участки откоса, состоящие из интеллектуальных объектов Land F / X, таких как растения и справочные заметки.
- Инструменты планирования: если вы запустите любое из следующих расписаний на чертеже, который включает одну или несколько областей уклона, инструмент планирования просканирует все заштрихованные области, относящиеся к этому графику, чтобы определить, находятся ли они внутри области уклона.Если это так, квадратные футы / метры, составляющие эти площади, будут пересчитаны вместе с (в большинстве случаев, за исключением случаев, указанных ниже) любыми соответствующими величинами или ставками на основе коэффициента уклона. К ним относятся:
- Завод и концептуальные ярлыки заводов (групповые, одиночные, соединительные линии и соединительные дуги): прикрытия и кустарники. На этикетках концептуальных растений также будут отмечены области концептуальных посадок, такие как смеси семян и трав. Примечание. Групповые метки потенциально могут включать растения в нескольких областях на разных склонах.
- Проверить метки для растений: если какие-либо почвопокровные или кустарниковые зоны находятся в пределах области уклона, инструмент изменит расчет количества растений в этих областях, чтобы включить коэффициент уклона, который может изменить существующую этикетку, если площадь уклона изменилась или добавлен после того, как метка была размещена. Примечание. Групповые метки потенциально могут включать растения в нескольких областях на разных склонах.
- Обозначения клапана: все области для капельной линии для пересчета расходов
Склоны также относятся к:
- Подобрать объект , Подобрать объект и Подобрать оборудование : если вы выберете обозначение или границу области уклона в качестве исходного объекта с одним из этих инструментов, размещенная вами дублирующая область также станет областью уклона.
- Пользовательская система координат ( UCS ): когда инструмент сканирует, находится ли область в пределах области уклона, сканирование будет совместимо с любой ПСК, установленной на чертеже.
- Внешние ссылки (Xrefs): расписания распознают обозначения уклона во внешних ссылках, пока внешняя ссылка находится на уровне L-SLOPE-AREA , а расписание настроено на включение внешних ссылок. Расписания, настроенные для включения внешних ссылок, также распознают участки откоса на живом чертеже, даже если объекты, рассчитанные по графику (например, растения), находятся во внешней ссылке.
- Обозначения площади: если вы запустите инструмент Обозначение площади и выберите штриховку или полилинию внутри области уклона, площадь будет рассчитана на основе уклона.
- Общая площадь : при расчете площади будут учитываться замкнутые полилинии в пределах области уклона.
Настройка обозначений области уклона
Обозначения зоны уклона по умолчанию выглядят так, как показано на рисунке выше.Если вы хотите настроить их внешний вид, вы можете отредактировать их исходные файлы в папке LandFX / blocks / graphics / callouts .
Вам нужно будет отредактировать только один исходный файл для каждой системы измерения. Исходный файл для обозначений имперской зоны откоса называется LAFX-SLOPE-AREA.dwg . Если вы используете метрическую систему, блок будет называться LAFX-SLOPE-AREA-M.dwg .
Имейте в виду, что условные обозначения области уклона по умолчанию не отображаются на графике и, как следствие, не отображаются на построенном чертеже.Вам нужно будет отредактировать их только в том случае, если вы хотите изменить их внешний вид в файле чертежа в том виде, в котором он отображается в САПР, или если вы планируете разместить их на назначенных слоях, чтобы они отображались в вашем чертеже.
Корректировка шкалы с помощью обозначений уклона
Если текст обозначения наклона становится слишком большим или слишком маленьким по сравнению с остальной частью вашего рисунка, вы, скорее всего, столкнулись с проблемой масштабирования. В этом случае следуйте нашим инструкциям, чтобы скорректировать масштаб в выносках.
Если вы хотите внести постоянные изменения в размер или масштаб всей выноски откоса при ее вставке в чертежи, вы можете сделать это, отредактировав исходные блоки выноски откоса.
Вебинары по теме
- Оценка A, B, C для ландшафтных архитекторов: следуйте инструкциям по основам простой оценки ландшафта. Мы рассмотрим некоторые простые концепции, такие как вычисление уклона и интерполяция горизонталей, и покажем вам, как использовать наши простые инструменты профилирования на реальном плане.(1 час 4 мин)
- Common Land F / X Вопросы. В этом веб-семинаре рассматриваются некоторые из наших малоизвестных инструментов, в том числе инструмент «Точечная отметка» и его связь с обозначениями откосов. (1 час)
- Профилирование и осушение. Изучите простые процессы профилирования с помощью наших инструментов аннотации, а также ознакомьтесь с некоторыми основами Civil 3D для более динамичного моделирования сайта. Мы рассмотрим, как автоматизировать рабочий процесс выставления оценок в соответствии с потребностями проекта.(1 час 2 минуты)
- Планы участков и Land F / X: Аарон Эмерсон из Mills Design Group покажет несколько отмеченных наградами тематических исследований того, как инструменты Land F / X Site, включая инструменты оценки, используются в его офисе. Аарон также поделится некоторыми важными уроками, извлеченными при настройке эффективного рабочего процесса дизайна сайта. (57 мин)
Устранение неполадок
Проблема: отметки точек и / или обозначения уклонов ориентированы неправильно или в неправильном направлении
Проблема: условные обозначения уклона остаются пустыми
Проблема: вы разместили обозначение уклона внутри рабочей области с назначенной ей ПСК, и выноска выровнена с этой ПСК, а не с WCS.
Проблема: сообщение об ошибке «За пределами пределов» в командной строке / вы не можете использовать обозначения уклона / не видите обозначения уклона в пространстве модели
Проблема: стрелки обозначения уклона полые, не сплошные или отображаются только в виде линий
Проблема: при редактировании обозначения отметки точки больше нельзя использовать инструмент обозначения откоса для автоматического обозначения откоса между двумя отметками отметки.
Проблема: вы получили ошибку недопустимого ввода при попытке разместить обозначение уклона
Последнее изменение пятница, 21 мая 2021 г., 16:53
Дифференциальные уравнения — Поля наклона
Поля наклона
Если вы построите его, они появятся.
Рассмотрим дифференциальное уравнение первого порядка
Мы не можем решить эту д.э. размышляя задом наперед, но мы все еще можем думать о том, как решить эту проблему. d.е. будет вести себя. Мы знаем, что это означает наклон y по отношению к x . Это означает, что любое решение этого дифференциального уравнения является функцией y , наклон которой в любой точке ( x , y ) функции равен x + y .
Мы собираемся вернуться к нотации Лейбница.
Пример задачи
Предположим, у нас есть решение y к д.э.
, который проходит через точку (2, 3):
Наклон y в точке (2, 3) должен быть
Хотя мы не знаем, что именно функция y выглядит так, мы знаем, что в точке (2, 3) наклон функции (и, следовательно, наклон ее касательной) равен 5:
Если у нас есть другое решение y для d.е.
, который проходит через точку (4, -1), наклон y в точке (4, -1) должен быть
Это означает, что касательная линия к y в точке (4, -1) имеет наклон 3:
Пример задачи
Предположим, что f является решением de
f ‘( x ) = 4 xy .
Если f проходит через точку (3, 10), то производная f в этой точке равна
4 (3) (10) = 120.
График с множеством маленьких касательных линий, подобный тому, который мы только что нарисовали, называется полем наклона или векторным полем . Поля наклона полезны для визуализации решений данного дифференциального уравнения. Если вы знаете, как ведет себя наклон функции, вы можете увидеть, как выглядит функция в целом.
Поскольку мы просто рисуем маленькие линии, рисование полей уклона немного скучно и утомительно. Если мы нарисуем поле наклона для д.э.
и включив больше точек, мы получим что-то вроде этого:
Мы уверены, что вы можете представить, как ужасно было бы вычислять все эти уклоны на этом рисунке вручную.К счастью, это то место, где обычно поощряется использование компьютеров для выполнения вашей работы.
Вот онлайн-инструмент для рисования полей уклона:
Вам будет предложено сопоставить поля уклона с их дифференциальными уравнениями или сопоставить дифференциальные уравнения с их полями уклона. Наша прогулка по полям склонов выше дала несколько примеров того, что вы можете искать. Вот несколько вопросов, которые вы можете задать себе, пытаясь сопоставить поля уклона и дифференциальные уравнения (вы можете задать эти вопросы, глядя на a d.е. или поле уклона):
Slope Fields and Solutions
Если у нас есть поле наклона для d.e. и точку в этом поле наклона, мы можем набросать решение, которое проходит через эту точку. Маленькие кусочки касательных похожи на стрелки, указывающие функции, в каком направлении двигаться. Если следовать по стрелкам, мы получим решение.
Пример задачи
Вот поле наклона для d.e.
и точка:
Нарисуйте решение, которое проходит через точку.
Ответ. Маленькие касательные линии очерчивают форму решения:
Когда мы используем поля наклона для наброска решений дифференциальных уравнений, решения не обязательно будут функциями.
Пример задачи
Вот поле наклона для d.e.
и точка:
Это не функция, потому что она не проходит тест вертикальной линии.
Это круто, потому что даже если мы не можем получить функцию одной переменной, которая является решением дифференциального уравнения, мы все равно можем увидеть форму решения на графике.
Поля наклона являются визуальным эквивалентом IVP для дифференциальных уравнений первого порядка. Поле уклона — это визуальный эквивалент дифференциального уравнения, а точка — визуальный эквивалент начального условия.
Мы можем нарисовать решение, которое проходит через точку, учитывая поле наклона и точку, потому что есть теорема единственности , которая гласит, что такая задача имеет ровно один ответ.
Вот причудливый математический язык, написанный как плохая поэзия:
Учитывая дифференциальное уравнение первого порядка и начальное условие
(при условии, что производная непрерывна)
существует ровно одно решение, которое удовлетворяет как дифференциальному уравнению, так и уравнению начальное состояние.Вот перевод полей уклона:
Для данного поля уклона и точки
(при условии, что производная непрерывна)
существует ровно одно решение, в котором
проходит через эту точку и имеет форму, заданную полем уклона. .Поскольку очень маловероятно, что вы когда-нибудь столкнетесь с такой проблемой, когда производная не является непрерывной, вы, вероятно, можете избежать мысли, что IVP, включающий дифференциальное уравнение первого порядка, имеет ровно одно решение.
Равновесные решения
Равновесный раствор представляет собой раствор д.э. производная которого всюду равна нулю. На графике равновесное решение выглядит как горизонтальная линия.
Учитывая поле наклона, мы можем найти равновесные решения, найдя везде, где горизонтальная линия вписывается в поле наклона.
Равновесные растворы бывают двух видов: стабильные и нестабильные. Эти термины легче всего понять, посмотрев на поля уклона.
Стабильное равновесное решение — это решение, к которому стремятся другие решения. Если мы выберем точку немного от равновесия в любом направлении, решение, которое проходит через эту точку, пытается прижаться к равновесному раствору.
Неустойчивое равновесное решение — это решение, от которого другие решения пытаются уйти.
- Постройте прямую линию с интервалом y
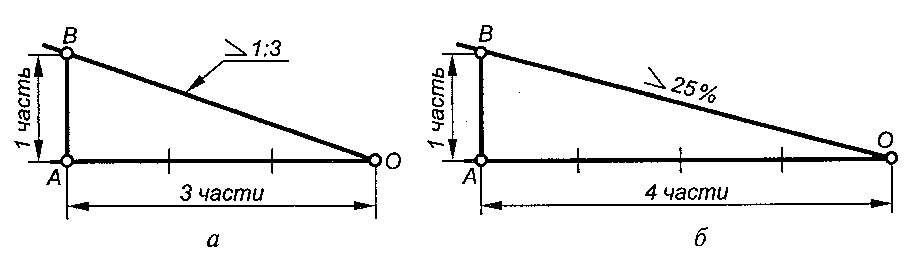 1
1 4
4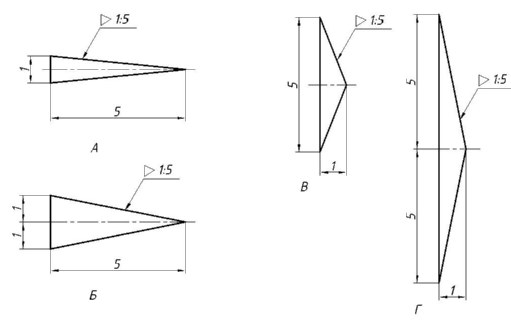


 Если чашу перевернуть вверх дном, дно (теперь верх) все еще будет точкой равновесия, потому что, если вы идеально сбалансируете шарик на вершине, он останется там. Точно так же с маятником, закрепленным внизу, если вы его идеально сбалансируете, он не будет двигаться. Однако в любом из этих случаев, если вы немного нарушите систему, она выйдет из равновесия и никогда не вернется сама по себе.
Если чашу перевернуть вверх дном, дно (теперь верх) все еще будет точкой равновесия, потому что, если вы идеально сбалансируете шарик на вершине, он останется там. Точно так же с маятником, закрепленным внизу, если вы его идеально сбалансируете, он не будет двигаться. Однако в любом из этих случаев, если вы немного нарушите систему, она выйдет из равновесия и никогда не вернется сама по себе. ПРОДУКТЫ}}
ПРОДУКТЫ}} AUTHOR_TOOLTIP_TEXT}}
AUTHOR_TOOLTIP_TEXT}}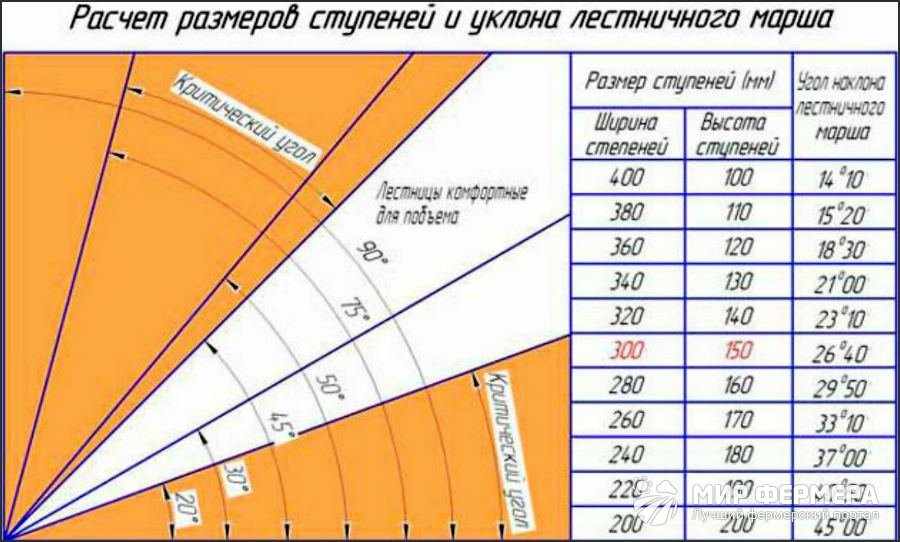
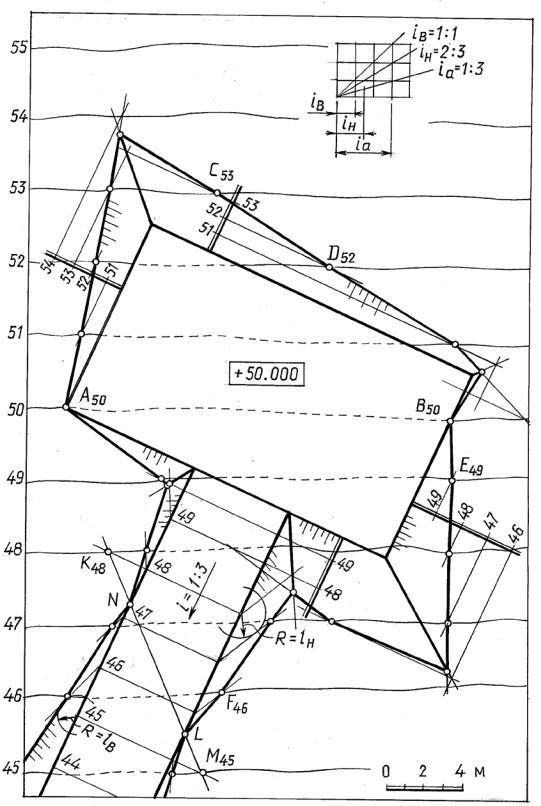 Если вам нужно больше отзывов о склоне, не стесняйтесь
Если вам нужно больше отзывов о склоне, не стесняйтесь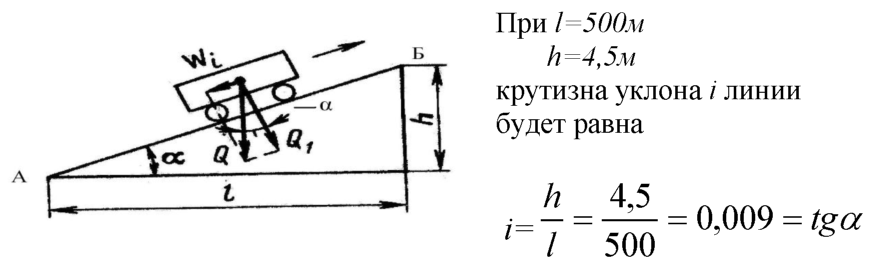
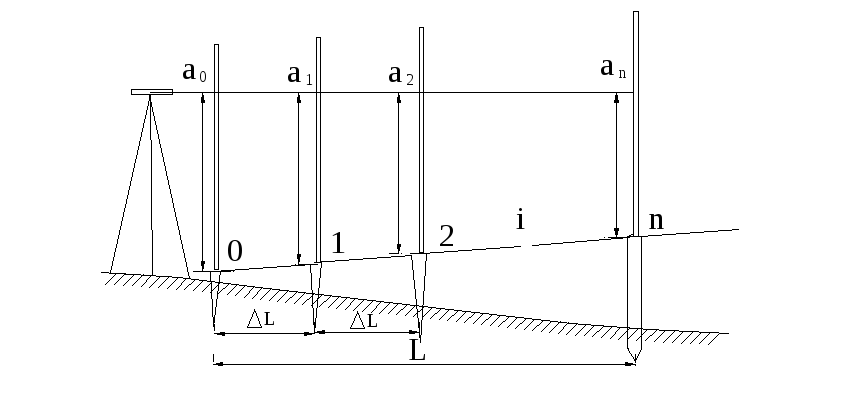
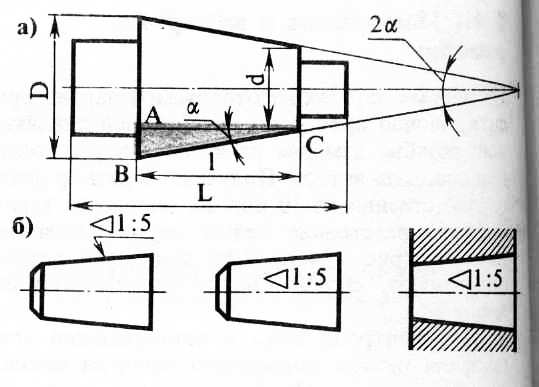

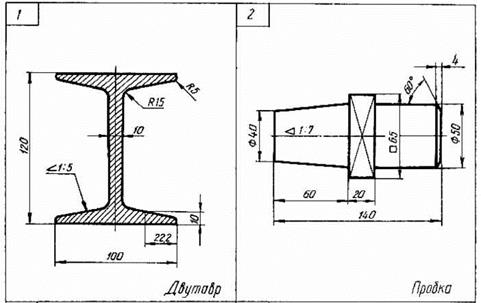
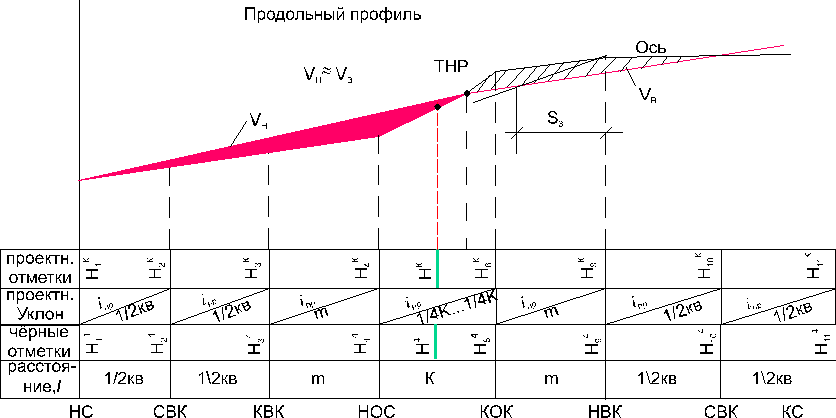

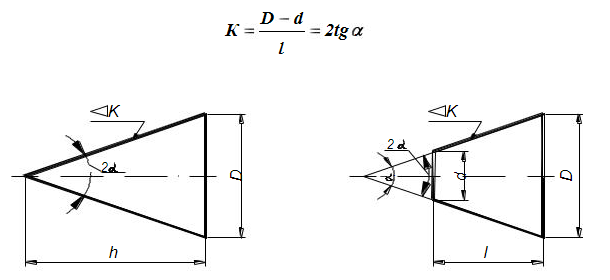 На шаге 1 мы нашли наш перехват y
На шаге 1 мы нашли наш перехват y