Линии и окружности черчение: ЧЕРЧЕНИЕ. Школьный интернет-учебник — Чтение чертежей 3-2
Содержание
Учебно-методическое пособие «Техника выполнения сопряжений» — Информио
Обмен опытом
Публикации
Методические разработки
Материалы конференции
Работы СНО
Персоналии
См. также:
Уважаемые коллеги. Размещение авторского материала на страницах электронного справочника «Информио» является бесплатным. Для получения бесплатного свидетельства необходимо оформить заявку
Положение о размещении авторского материала
Размещение информации
31.10.2013
110229
241409
Ларионова Елена Владимировна, преподаватель
Букова Ольга Михайловна, преподаватель спецдисциплин
Иркутский авиационный техникум
При изучении дисциплины «Начертательная геометрия и
инженерная графика» студенты должны усвоить правила и последовательность
выполнения геометрических построений и сопряжений. В этом отношении лучшим
В этом отношении лучшим
способом приобретения навыков построения являются задания по вычерчиванию
контуров сложных деталей.
Прежде чем приступить к выполнению контрольного задания,
нужно изучить технику выполнения геометрических построений и сопряжений по
методическому пособию.
Сопряжением называется
плавный переход от одной линии к другой. Для построения любого сопряжения дугой
заданного радиуса нужно найти:
- Центр
сопряжения – центр, из которого проводят дугу; - Точки
сопряжения (касания) – точки, в которых одна линия переходит в другую.
Центр сопряжения
находится от точек сопряжения на одинаковых расстояниях, равных радиусу
сопряжения R. Переход от прямой к
окружности будет плавным в том случае, если прямая касается к окружности. Точка
сопряжения К лежит на перпендикуляре, опущенном из центра О окружности к прямой
(рис.
1)
рис. 1
Переход от одной
окружности к другой будет плавным, если окружности касаются.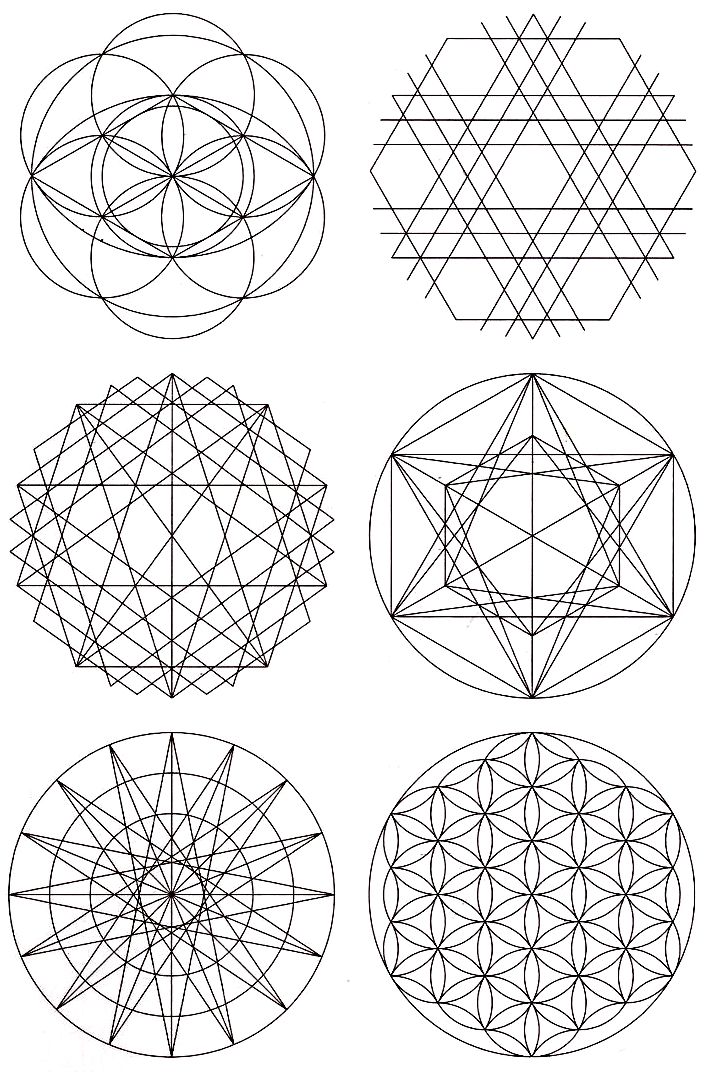
Различают два случая
касания дуг окружностей: внешнее (рис.
2) и внутреннее (рис.3).
При внешнем касании
центры окружностей лежат по разные стороны от их общей касательной L (рис. 2). Расстояние между их центрами ОО1 равно
сумме радиусов окружностей R+R1 и точка касания лежит на прямой ОО1,
соединяющей их центры.
При внутреннем касании
центры окружностей лежат по одну сторону от их общей касательной L. Расстояние
между их центрами ОО1 равно разности их радиусов R-R1 и точка касания К окружностей
лежит на продолжении прямой ОО1 (рис.
3).
рис. 2 | рис. 3 |
Касание дуг окружностей:
рис.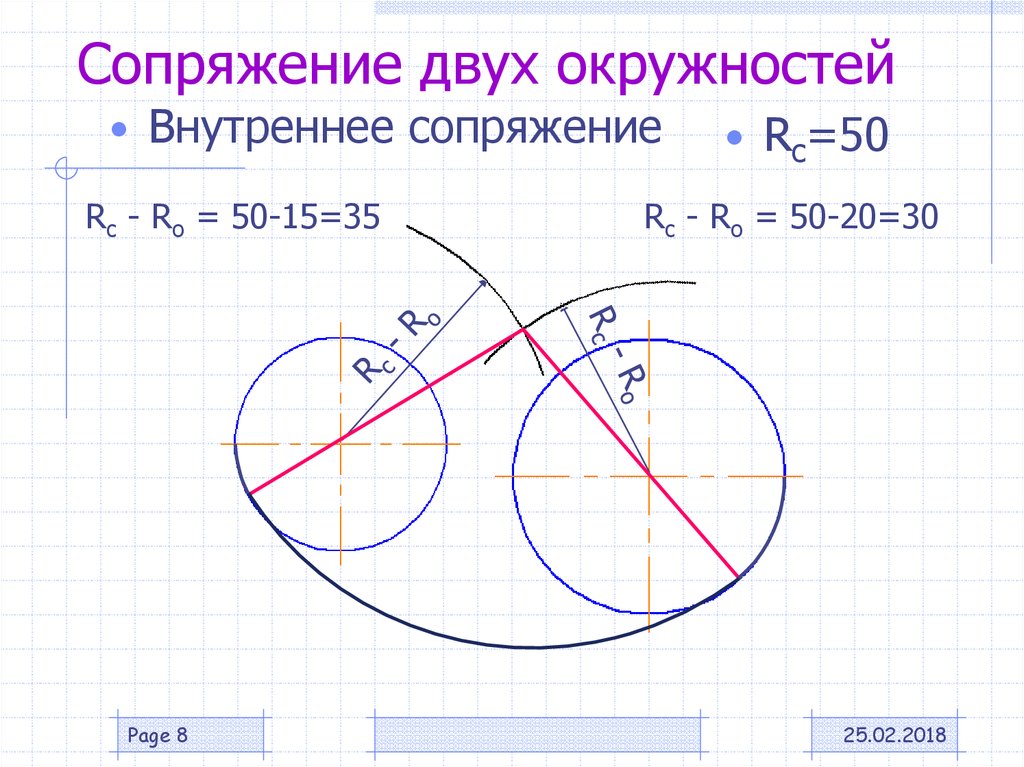 2 – сопряжение двух окружностей (внешнее касание)
2 – сопряжение двух окружностей (внешнее касание)
рис. 3 – сопряжение двух окружностей (внутреннее касание)
Сопряжение двух пересекающихся прямых
Даны
пересекающиеся под прямым, острым и
тупым углами прямые линии.
Требуется построить сопряжения этих прямых дугой заданного
радиуса R.
рис. 4
- Для
нахождения центра сопряжения проводят вспомогательные прямые, параллельные
данным на расстоянии равном радиусу R. Точка пересечения этих прямых т.О и
будет центом дуги сопряжения (рис.
4). - Перпендикуляры,
опущенные из центра дуги сопряжения т.О на данные прямые, определяют точки
касания К и N. - Из
точки О, как центра, описывают дугу заданного радиуса R.
рис. 5
Примечание.Для
прямых углов центр сопряжения удобнее находить с помощью циркуля (рис. 5).
Сопряжение дуги окружности и прямой
линии дугой заданного радиуса.
Внешнее касание
Дана окружность радиуса
R и прямая АВ. Требуется соединить их дугой
радиусом R1.
рис. 6
- Для
нахождения центра сопряжения из центра О заданной окружности проводят дугу m радиуса R + R1 и
на расстоянии R1 – прямую n // AB. Точка О1 пересечения прямой n и дуги m будет центром
сопряжения. - Для
получения точек сопряжения: К и К1 проводят линию центров ОО1 и
восстанавливают к прямой АВ перпендикуляр ОК1. - Из
центра сопряжения О1 между точками К и К1 проводят дугу сопряжения радиусом R1
Внутреннее касание
В случае внутреннего
касания выполняют те же построения, но дугу m
вспомогательной окружности проводят радиусом R — R1.
рис. 7
7
Сопряжение двух окружностей дугой
заданного радиуса
Заданы две окружности
радиусом R1 и R2. Требуется построить сопряжение дугой
заданного радиуса R.
рис. 8
Внешнее касание
- Для
определения центра сопряжения О проводят вспомогательные дуги: из центра О1окружности радиусом R + R1 и из центра О2 окружности радиуса R
+ R2. Точка О пересечения этих дуг является центом сопряжения. - Соединяя
центры О и О1, а так же О и О2 , определяют точки
сопряжения (касания) К1 и К2. - Из
центра О радиусом R проводят дугу сопряжения между точками К1
и К2
Внутреннее касание
При внутреннем касании
выполняют те же построения, но дуги проводят радиусами
R -R1 и R — R2.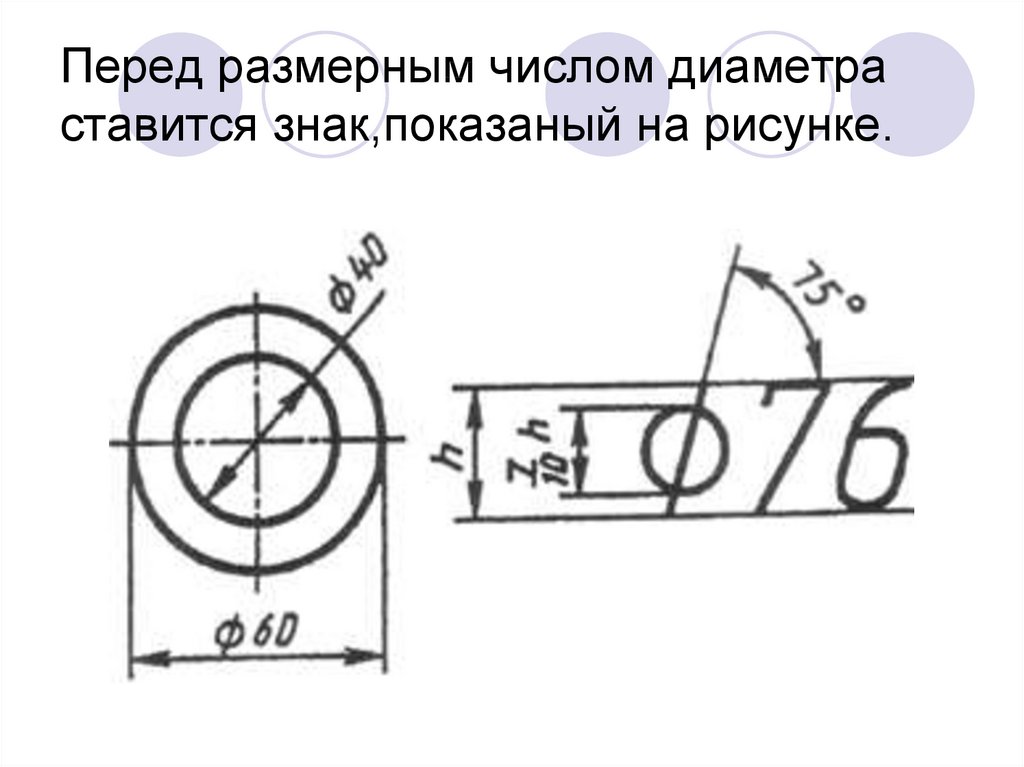
рис. 9
Смешанное касание
рис. 10
Центр сопряжения О
находится в пересечении двух дуг, описанных из центра О1 радиусом R
— R1 и из центра О2 радиусом R + R2
Примечание. При
смешанном сопряжении центр О1 одной из сопрягаемых дуг лежит внутри
сопрягающей дуги радиуса R , а центр О2 другой дуги – вне ее.
Частные случаи
Нахождение
центра дуги заданного радиуса.
Задана дуга радиусом R,
соединяющая две параллельные прямые mи n и проходящая через точку А ∈ m (рис. 11). Требуется найти центр О заданной дуги.
рис. 11
В основу построения положено нахождение
точки О, равноудаленной от заданных прямых (рис.
11).
- Из
точки А ∈ m, как из центра, проводят дугу
вспомогательной окружности с заданным радиусом R.
- Проводят
вспомогательную прямую l,
параллельную прямой n, на
расстоянии, равном заданному радиусу R. - Точка О – точка пересечения этих
вспомогательных линий является центром заданной дуги. (рис. 12)
рис. 12
- Боголюбов
С.К. Инженерная графика: Учебник для средних специальных учебных заведений. –
3-е изд., испр. И доп. — М.: Машиностроение, 2006. – с.392: ил. - Куприков
М.Ю. Инженерная графика: учебник для ССУЗов – М.: Дрофа, 2010 – 495 с.: ил. - Федоренко
В.А., Шошин А.И. Справочник по машиностроительному черчению Л.: Машиностроение.
1976. 336 с.
Расскажите друзьям:
Назад к списку
Сопряжение окружностей, сопряжение углов, сопряжение линий, сопряжение дуг ChertimVam.Ru
В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.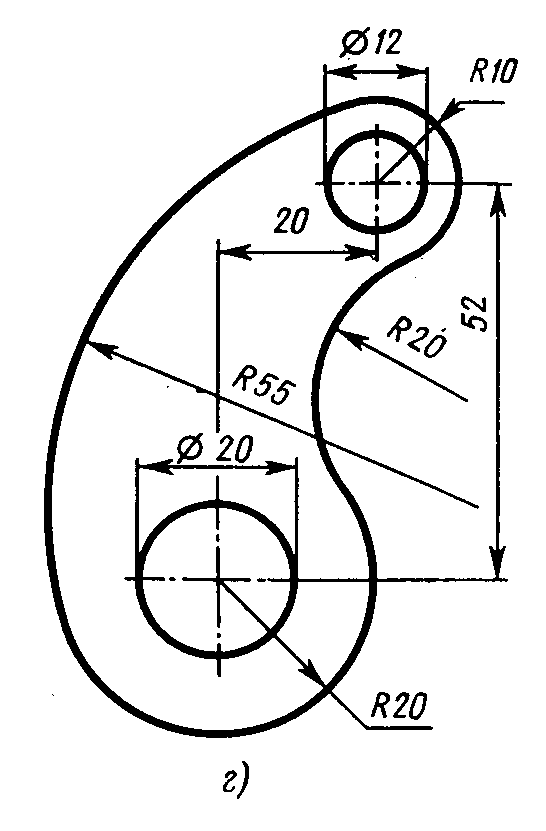
Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.
Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.
Ниже будут рассмотрены основные типы сопряжений.
Сопряжение углов (Сопряжение пересекающихся прямых)
Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом.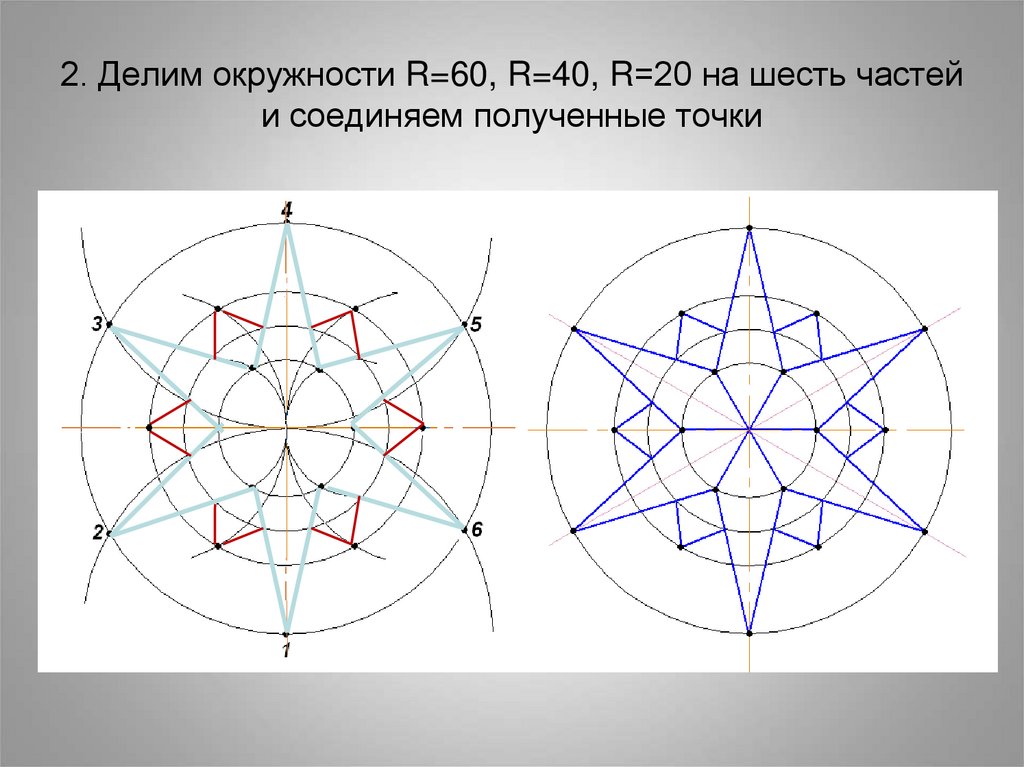 Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.
Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.
Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)
Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.
Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)
Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.
Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.
Сопряжение параллельных прямых линий
Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.
Сопряжение окружностей(дуг) с прямой линией
Внешнее сопряжение дуги и прямой линии
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.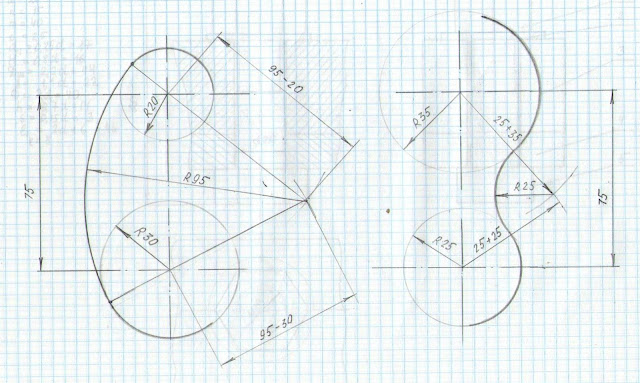
Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности OR радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой Оr.
Из центра сопряжения, точки Оr, опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности ОR и центр сопряжения Оr линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.
Внутреннее сопряжение прямой линии с дугой
По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности OR радиусом R-r.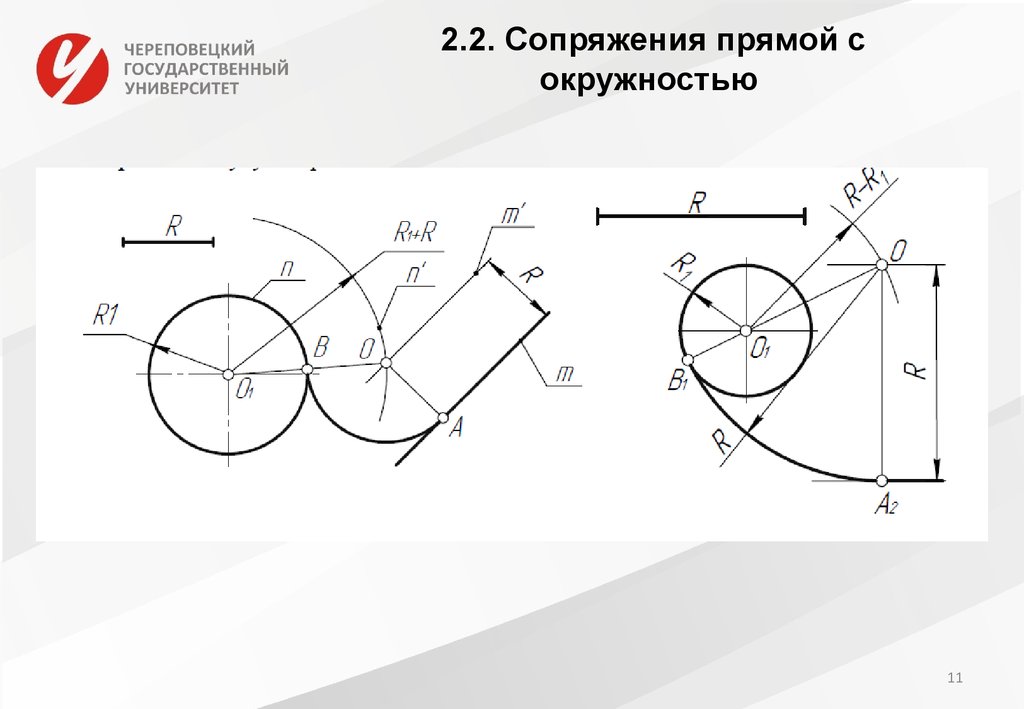 Точка Оr, полученная на пересечении прямой и дуги, и будет центром сопряжения.
Точка Оr, полученная на пересечении прямой и дуги, и будет центром сопряжения.
Из центра сопряжения(точка Оr) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.
Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности ОR прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки Оr, центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.
Сопряжение окружностей (дуг)
Внешнее сопряжение дуг окружностей
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно.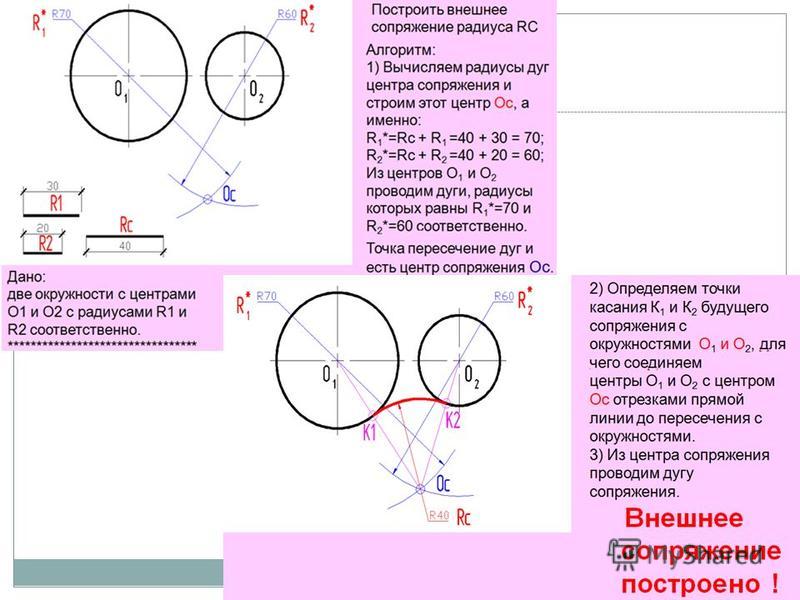 Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.
Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.
Внутреннее сопряжение дуг окружностей
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.
Смешанное сопряжение дуг окружностей
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.
Рисование линий и окружностей — Компьютерная графика
Фундаментальной операцией в компьютерной графике является рисование линий и окружностей.
Например, они используются в качестве компонентов масштабируемых шрифтов и векторной графики;
буква «г» указана как серия линий и кривых,
так что, когда вы увеличиваете его, компьютер может перерисовать его в любом необходимом разрешении.
Если бы система сохраняла пиксели только для формы буквы, то увеличение масштаба привело бы к низкому качеству изображения.
Точки, использованные для создания буквы «g» в логотипе Google.
В 3D-графике формы часто сохраняются с помощью линий и кривых, которые обозначают края крошечных плоских поверхностей (обычно треугольников), каждая из которых настолько мала, что вы не можете их увидеть, если не увеличите масштаб.
Линии и окружности, определяющие объект, обычно задаются числами (например, линия между заданной начальной и конечной позицией или окружность с заданным центром и радиусом).
Исходя из этого, графическая программа должна вычислить, какие пиксели на экране должны быть окрашены, чтобы представить линию или круг, или ей может просто понадобиться определить, где находится линия, не рисуя ее.
Например, вот увеличенная сетка пикселей с 5 линиями.
Вертикальная линия должна быть указана как идущая от пикселя (2, 9) к (2, 16), то есть начиная с 2 поперек и 9 вверх и заканчивая 2 поперек и 16 вверх.
Конечно, это лишь малая часть экрана, так как обычно они больше похожи на 1000 на 1000 пикселей и более; даже экран смартфона имеет сотни пикселей в высоту и ширину.
Это вещи, которые легко сделать карандашом и бумагой с помощью линейки и циркуля, но на компьютере вычисления нужно делать для каждого пикселя, и если использовать неправильный метод, то это займет слишком много времени и изображение будет отображаться медленно или живая анимация будет прерывистой.
В этом разделе мы рассмотрим несколько очень простых, но умных алгоритмов, позволяющих компьютеру выполнять эти вычисления очень быстро.
13.3.1.
Штриховой рисунок
Чтобы нарисовать линию, компьютер должен вычислить, какие пиксели нужно заполнить, чтобы линия выглядела ровно.
Вы можете попробовать это, раскрашивая квадраты на сетке, такой как показанная ниже (они во много раз больше, чем пиксели на обычном принтере или экране).
Мы идентифицируем пиксели в сетке, используя два значения ( x , y ), где x — это расстояние слева, а y — это расстояние вверх от низа.
Нижний левый пиксель ниже — (0, 0), а верхний правый — (19, 19).
Попробуйте нарисовать эти прямые линии, нажимая на пиксели в следующей сетке:
- от (2, 17) до (10, 17)
- с (18, 2) по (18, 14)
- с (1, 5) по (8, 12)
Начертить горизонтальную, вертикальную линию или линию под углом 45 градусов, как показано выше, очень просто; это те, под разными углами, которые требуют некоторого расчета.
Можете ли вы, не используя линейку, провести прямую линию от А до В на следующей сетке, раскрасив ее в пикселях?
Когда вы закончите рисовать линию, попробуйте проверить ее с помощью линейки.
Поместите линейку так, чтобы она проходила из центра A в центр B.
Пересекает ли он все пиксели, которые вы закрасили?
13.3.2.
Использование формулы для рисования линии
Математическая формула для линии .
Это дает вам значение y для каждого значения x на экране,
и вы можете указать две вещи:
наклон линии,
который ,
и где линия пересекает и ось, то есть .
Другими словами, когда ваша линия занимает экран размером x пикселей, цветной пиксель будет (, ).
Например, выбор и означает, что линия будет проходить через точки (0, 3), (1, 5), (2, 7), (3, 9) и так далее.
Эта линия поднимается вверх на 2 пикселя для каждого пикселя и пересекает ось Y на 3 пикселя вверх ().
Вам следует поэкспериментировать с рисованием графиков для различных значений и (например, начните с и попробуйте эти три строки: , и ), вставляя значения.
Под каким углом расположены эти линии?
Формулу можно использовать для определения того, какие пиксели должны быть окрашены для линии, проходящей между и .
Что такое и для точек A и B на сетке ниже?
Посмотрите, сможете ли вы вычислить значения и для линии от А до В, или вы можете рассчитать их, используя следующие формулы:
Теперь нарисуйте ту же линию, что и в предыдущем разделе (между А и В), используя формулу для расчета для каждого значения от до (вам нужно будет округлить до ближайшего целого числа, чтобы определить, какой пиксель нужно закрасить).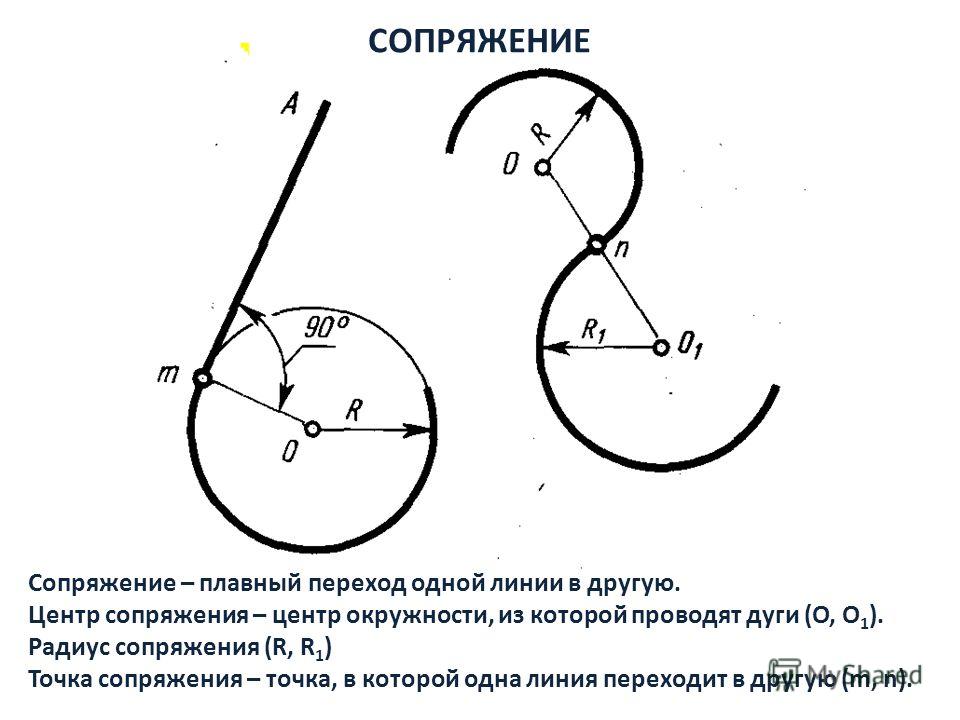
Если формулы были применены правильно, значение должно находиться в диапазоне от до .
Закончив линию, проверьте ее с помощью линейки.
Как это по сравнению с вашей первой попыткой?
Теперь посчитайте количество вычислений, необходимых для отработки каждой точки.
Кажется, что их немного, но помните, что компьютер может вычислять сотни точек на тысячах линий сложного изображения.
Хотя эта формула прекрасно работает, она слишком медленная для создания сложной графики, необходимой для хороших анимаций и игр.
В следующем разделе мы рассмотрим метод, который значительно ускоряет это.
13.3.3.
Алгоритм линии Брезенхэма
Более быстрый способ для компьютера вычислить, какие пиксели нужно закрасить, — это использовать линейный алгоритм Брезенхэма.
Он следует этим простым правилам.
Сначала вычислите эти три значения:
Чтобы нарисовать линию, заполните начальный пиксель, а затем для каждой позиции вдоль оси x :
- Если меньше 0, нарисуйте новый пиксель на той же линии, что и исходный.
 последний пиксель и добавить в .
последний пиксель и добавить в . - Если было 0 или больше, нарисуйте новый пиксель на одну строку выше, чем последний пиксель, и добавьте к .
- Повторяйте это решение, пока не дойдете до конца строки.
Не используя линейку, используйте алгоритм линий Брезенхема, чтобы нарисовать прямую линию от A до B:
После того, как вы закончите линию, проверьте ее с помощью линейки.
Как это по сравнению с предыдущими попытками?
13.3.4.
Линии под другими углами
До сих пор версия алгоритма рисования линий Брезенхэма, которую вы использовали, работала только для линий, которые имеют градиент (наклон) от 0 до 1 (то есть от горизонтали до 45 градусов).
Чтобы сделать этот алгоритм более общим, чтобы его можно было использовать для рисования любой линии, необходимы некоторые дополнительные правила:
- Если линия наклонена вниз, а не вверх, то, когда P равно 0 или больше, нарисуйте пиксель следующего столбца на одну строку ниже предыдущего пикселя, а не выше его.

- Если изменение значения больше, чем изменение значения (что означает, что наклон больше 1), то необходимо изменить расчеты для A, B и исходное значение для P.
При расчете A, B и начального P используйте X вместо Y, и наоборот.
При рисовании пикселей вместо того, чтобы проходить через каждый столбец по оси X, просматривайте каждую строку по оси Y, рисуя по одному пикселю в строке.
В приведенной выше сетке выберите две собственные уникальные точки.
Не просто выбирайте точки, которые дадут горизонтальные или вертикальные линии!
Теперь используйте алгоритм Брезенхэма, чтобы нарисовать линию.
Убедитесь, что он дает те же точки, которые вы бы выбрали, используя линейку или формулу.
Сколько арифметических вычислений (умножений и сложений) потребовалось для алгоритма Брезенхема?
Сколько их потребовалось бы, если бы вы использовали формулу?
Что быстрее (имейте в виду, что сложение выполняется намного быстрее, чем умножение для большинства компьютеров).
Вы можете написать программу или спроектировать электронную таблицу для выполнения этих вычислений за вас — этим должны заниматься программисты графики.
13.3.5.
Круги
Помимо прямых линий, еще одной распространенной формой, которую часто приходится рисовать компьютерам, являются круги.
Алгоритм, аналогичный алгоритму рисования линии Брезенхэма, называемый алгоритмом средней точки круга, был разработан для эффективного рисования круга.
Окружность определяется центральной точкой и радиусом.
Точки на окружности — это все радиусное расстояние от центра окружности.
Попробуйте нарисовать круг вручную, заполняя пиксели (без использования линейки или циркуля).
Обратите внимание, как трудно заставить круг выглядеть круглым.
Можно нарисовать круг, используя формулу, основанную на теореме Пифагора, но для этого требуется вычисление квадратного корня для каждого пикселя, что очень медленно.
Следующий алгоритм намного быстрее и включает в себя только простую арифметику, поэтому он быстро работает на компьютере.
13.3.6.
Алгоритм окружности срединной точки Брезенхэма
Вот правила для алгоритма средней точки окружности для окружности (, ) с радиусом :
Повторяйте следующие правила по порядку, пока не станет больше:
- Заполните пиксель с координатой (, )
- Увеличить на
- Увеличение на 1
- Если больше или равно 0, вычтите из , а затем вычтите 1 из .

Следуйте правилам, чтобы нарисовать круг на сетке, используя (, ) в качестве центра круга и радиуса.
Обратите внимание, что он нарисует только начало круга, а затем остановится, потому что больше, чем !
Когда становится больше , рисуется одна восьмая (октант) круга.
Оставшуюся часть круга можно нарисовать, отражая уже имеющийся у вас октант (вы можете думать об этом как о повторении схемы шагов, которые вы только что сделали, в обратном порядке).
Вы должны отражать пиксели по осям X и Y так, чтобы линия отражения пересекала середину центрального пикселя круга.
Половина круга теперь нарисована, левая и правая половина.
Чтобы добавить оставшуюся часть круга, необходимо использовать другую линию отражения.
Можете ли вы решить, какая линия отражения необходима, чтобы завершить круг?
Квадранты и октанты
Жаргон Бастер
Квадрант – это четверть площади; четыре квадранта, покрывающие всю площадь, отмечены пересекающимися вертикальной и горизонтальной линиями.
Октант составляет одну восьмую площади, а 8 октантов размечены 4 линиями, которые пересекаются в одной точке (вертикальной, горизонтальной и двумя диагональными линиями).
Чтобы завершить круг, нужно отразить по диагонали.
Линия отражения должна иметь наклон 1 или -1 и должна пересекать середину центрального пикселя круга.
Хотя использование линии отражения на октанте более понятно для человека, компьютер может рисовать все отраженные точки одновременно с рисованием точки в первом октанте, потому что когда он рисует пиксель со смещением (x,y) от центра круга, он также может рисовать пиксели со смещением (x, -y), (-x, y), (-x, -y), (y, x), (y , -x), (-y, x) и (-y, -x), которые дают все восемь отражений исходной точки!
Кстати, такой алгоритм можно адаптировать для рисования эллипсов, но он должен рисовать целый квадрант, потому что в эллипсе нет октантной симметрии.
13.3.7.
Практическое применение
Компьютеры должны рисовать линии, окружности и эллипсы для самых разных задач, от игровой графики до линий на архитектурном чертеже и даже крошечного круга для точки над буквой «i» в текстовом процессоре.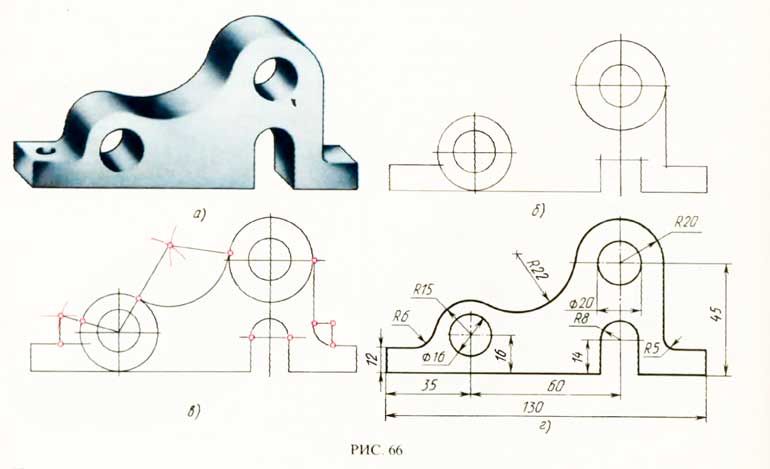
Комбинируя рисование линий и кругов с такими методами, как «заполнение» и «сглаживание», компьютеры могут рисовать гладкие, четкие изображения, не зависящие от разрешения.
Когда изображение на компьютере описывается как контур с заливкой цветом, это называется векторной графикой — ее можно перерисовывать при любом разрешении.
Это означает, что с векторным изображением увеличение изображения не приведет к пикселизации, наблюдаемой при увеличении растровой графики, которая сохраняет только пиксели и, следовательно, увеличивает пиксели при увеличении.
Однако в векторной графике пиксели пересчитываются каждый раз, когда изображение перерисовывается, и поэтому важно использовать быстрый алгоритм, подобный приведенному выше, для рисования изображений.
Контурные шрифты — одно из наиболее распространенных применений векторной графики, поскольку они позволяют увеличивать размер текста до очень больших размеров без потери качества формы букв.
Ученые-компьютерщики нашли быстрые алгоритмы для рисования и других фигур, а это означает, что изображение появляется быстро, а графика может быстро отображаться на относительно медленном оборудовании — например, смартфону необходимо все время выполнять эти вычисления для отображения изображений, а уменьшение количества вычислений может продлить срок службы батареи, а также ускорить его отображение.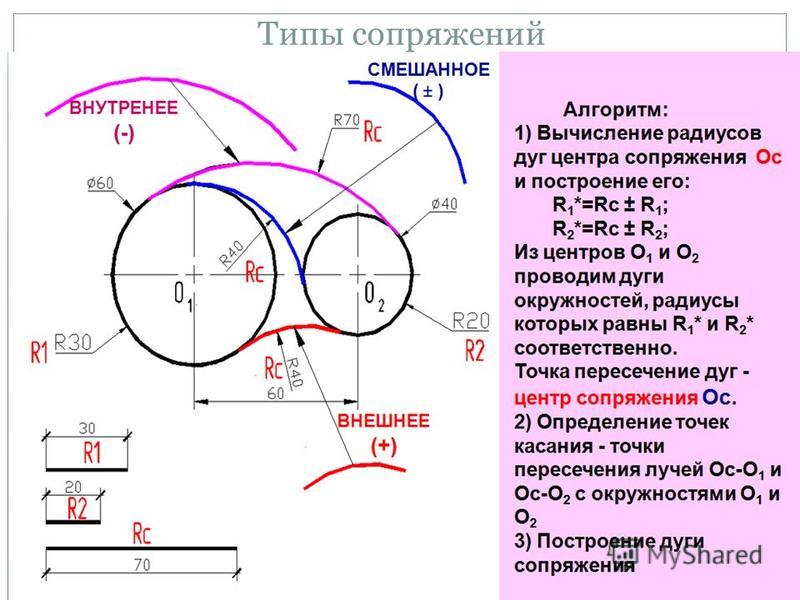
Как обычно, все не так просто, как показано здесь.
Например, рассмотрим горизонтальную линию, которая идет от (0, 0) до (10, 0) и имеет 11 пикселей.
Теперь сравните это с линией под углом 45 градусов, которая идет от (0, 0) до (10, 10).
Он по-прежнему имеет 11 пикселей, но линия длиннее (если быть точным, примерно на 41% длиннее).
Это означает, что линия будет казаться тоньше или тусклее на экране, и необходимо проделать дополнительную работу (в основном сглаживание), чтобы линия выглядела нормально.
Мы только начали изучать, какие методы в графике необходимы для быстрого рендеринга высококачественных изображений.
Рисование линии и круга
Проект
Чтобы сравнить метод Брезенхэма с использованием уравнения прямой (), выберите свою собственную начальную и конечную точки линии (конечно, убедитесь, что они находятся под интересным углом) и покажите расчеты, которые будут выполнены каждым методом.
Подсчитайте количество сложений, вычитаний, умножений и делений, которые выполняются в каждом случае, чтобы сделать сравнение.
Обратите внимание, что сложение и вычитание обычно намного быстрее, чем умножение и деление на компьютере.
Вы можете оценить, сколько времени занимает каждая операция на вашем компьютере, запустив программу, которая выполняет тысячи операций и засечет, сколько времени занимает каждая операция.
Исходя из этого, вы можете оценить общее время, затрачиваемое каждым из двух методов.
Хорошим показателем для них является то, сколько строк (выбранной вами длины) ваш компьютер может вычислить в секунду.
Если вы оцениваете скорость рисования круга, вы можете сравнить количество операций сложения и умножения с числом операций, требуемых формулой Пифагора, которая является основой для простого уравнения окружности (для этого расчета линия из центра круга к определенному пикселю на краю — это гипотенуза треугольника, а две другие стороны — это горизонтальная линия от центра и вертикальная линия до точки, которую мы хотим найти.
Вам нужно будет рассчитать y значение для каждого значения x ; длина гипотенузы всегда равна радиусу).
Предыдущий:
Графические преобразования
Далее:
Вся история!
Упражнение по рисованию — круги и линии из моего альбома для рисования — блог Кэрол по рисованию
Итак, я рисовал, занимаясь своими делами, когда вдруг понял, что открыл для себя новое упражнение по рисованию, которое помогло мне увидеть больше точно при рисовании с натуры! Я думаю, что это сделает то же самое и для вас, так что вот оно.
Вам понадобится шаблон круга любого размера. У меня есть один, сделанный из картона, и я храню его в конце своего альбома для рисования.
Для начала просто нарисуйте два или три круга рядом друг с другом. Я нарисовал здесь два примера. Попробуйте перекрыть один набор кругов.
Теперь добавьте линии, соединяющие круги.
Правил нет. Вы можете использовать шаблон круга, чтобы сделать дополнительные линии, использовать французские кривые или просто посмотреть на них.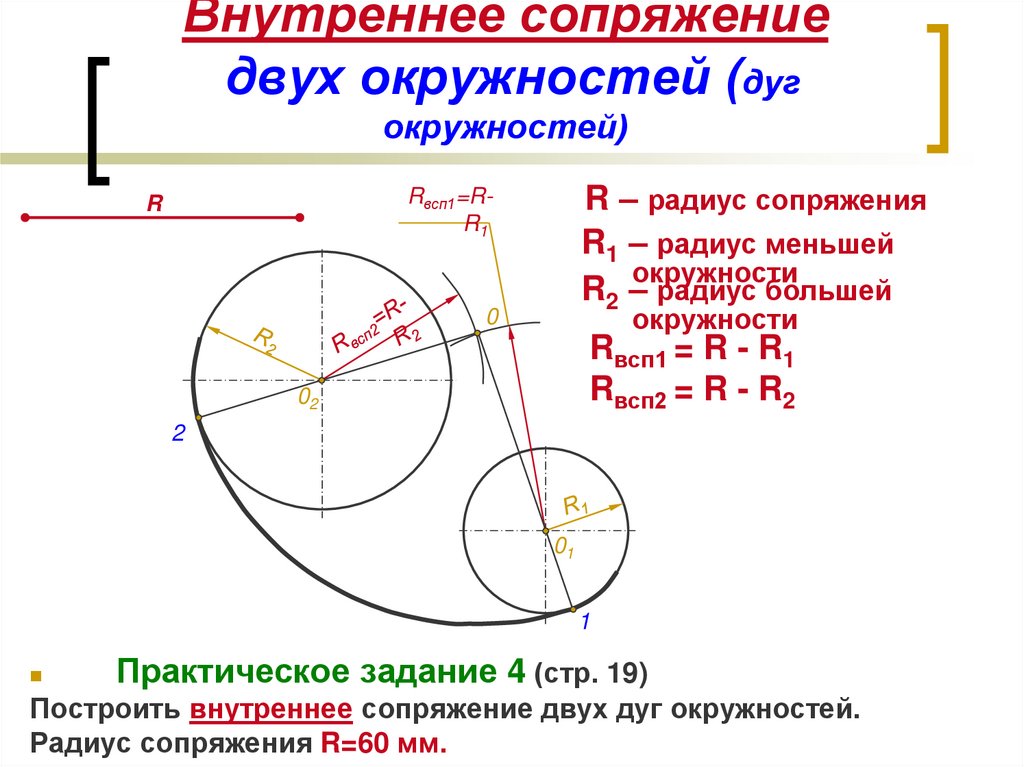
Стирание нескольких линий может изменить весь вид, посмотрите на фигуру справа, так что попробуйте и это.
В примере А слева я работал с линией. В примере B я работал со сплошными формами и получил совершенно другой вид, который я подчеркнул штриховкой.
Вот несколько заметок, которые я сделал во время работы и которые могут быть вам полезны:
- Аккуратность не в счет. Сделайте много линий, прежде чем выбрать правильную, а затем сотрите остальные.
- Я часто нахожу что-то новое, чтобы попробовать в следующем рисунке, делая интересные ошибки в текущем.
- К сожалению, не забудьте нарисовать круги посередине листа, чтобы у вас было достаточно места для рисования вокруг них.
- Поверните лист и посмотрите на рисунок со всех сторон. Кроме того, легче повернуть бумагу, чтобы нарисовать хорошую дугу, чем согнуть руку.
- Следуйте своим инстинктам.
- Или пойти против своих инстинктов и попытаться восстановиться.
 Идеи, рожденные отчаянием, выталкивают вас из зоны комфорта.
Идеи, рожденные отчаянием, выталкивают вас из зоны комфорта.
Рисовать с натуры стало немного проще – даже спустя столько лет.
Практика, которую я приобрела, визуализируя каждую линию, прежде чем рисовать ее, была волшебным импульсом, который я чувствовал, когда рисовал с натуры. Я мог гораздо легче, чем обычно, определять основную абстрактную форму объектов и мог проектировать дуги и углы, которые соединили бы один объект с другим, если бы я продолжил эти линии в уме.
Я обнаружил, что работаю с более единым видением отношений, и было чудесно отказаться от взгляда на вещи «по частям» и уступить место взгляду на все в целом.
Серия круглых рисунков из моего альбома для рисования
Этот рисунок начинался как два простых круга, один поверх другого. Я знаю, ты видишь нижний. Я стер нижнюю половину верхней, чтобы она соответствовала дизайну.
Идея заключалась в том, чтобы просто найти способ объединить два круга с помощью кривых, которые мне понравились, и ничего более.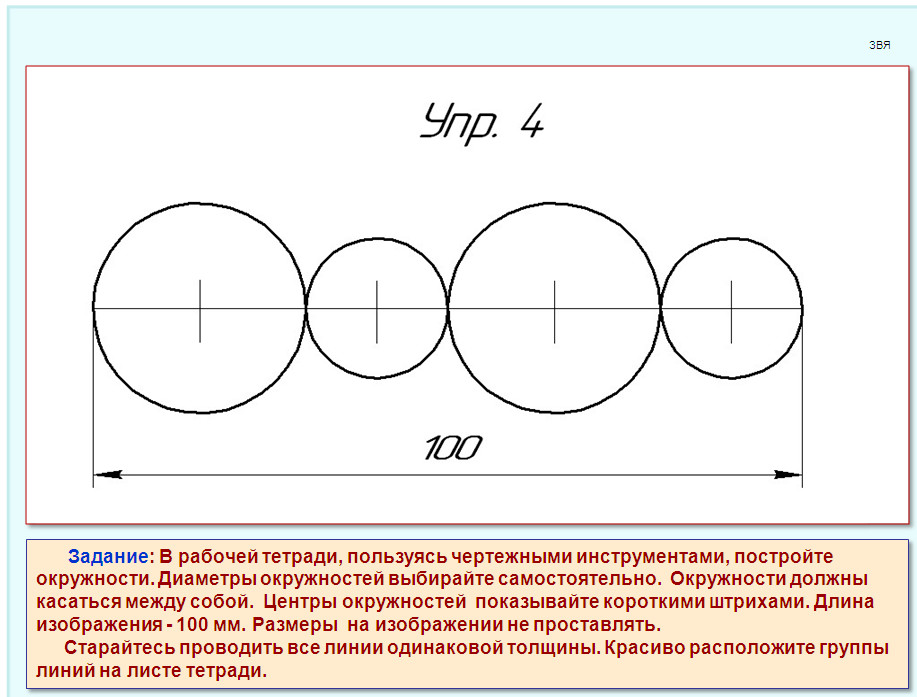
Я называю это Музыкой, потому что промежутки между строками имеют хороший ритм.
Я называю это Танцем, потому что оно трехмерное. Его основание состояло из трех кругов, один из которых перекрывал два нижних.
Когда я пытался визуализировать, как объединить эти три перекрывающихся круга, я решил «поднять» некоторые линии со страницы. Затем мне нужно было найти способ превратить новые пространства в прекрасные формы, в то же время изгибая новые линии, чтобы сформировать изящные соединения между кругами.
Я использовал всего несколько линий, чтобы соединить эти круги, а затем я хотел посмотреть, что определяет края линии с штриховкой, добавленной к форме.
Мне нравится, как штриховка сглаживает края и делает каждую часть отдельной, но мне также нравится, как штриховка объединяет весь рисунок, когда взгляд перемещается по нему.
Исчерпав умные имена, я просто называю это Три.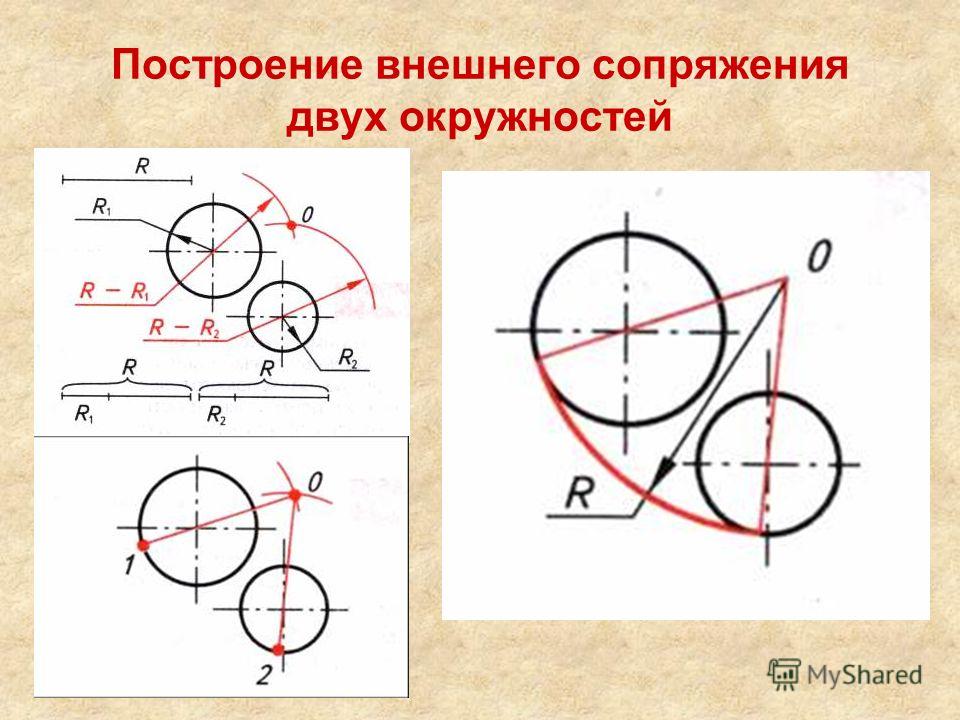
 последний пиксель и добавить в .
последний пиксель и добавить в .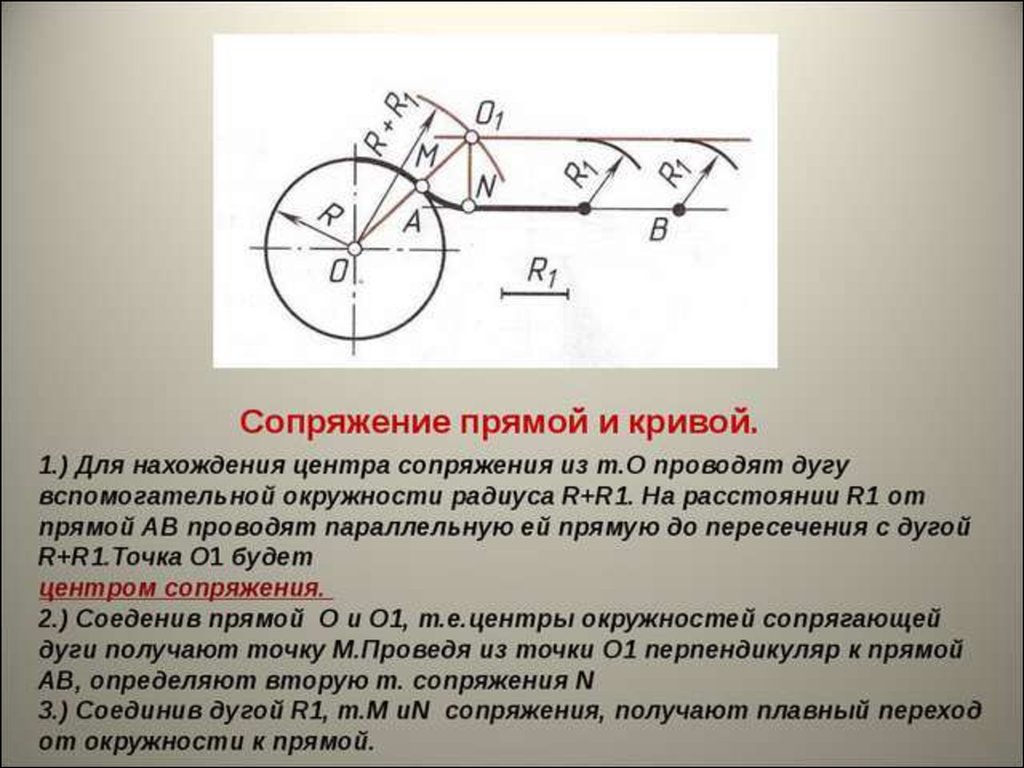

 Идеи, рожденные отчаянием, выталкивают вас из зоны комфорта.
Идеи, рожденные отчаянием, выталкивают вас из зоны комфорта.