Сечение как построить: Построение сечений
Содержание
Сечения — Умскул Учебник
На этой странице вы узнаете
- Как дракон с помощью сечений разрушал город?
- Чем вода похожа на сечение?
- Что общего у следа на снегу и следа в сечении?
Заглянем в кинотеатр имени Математики. Какой фильм сейчас будут показывать? Располагайтесь поудобнее, приятного просмотра…
Сечения
Как дракон с помощью сечений разрушал город?
…В далеком будущем, на одной из недавно открытых планет, люди построили новую цивилизацию. Они возвели новые дома для комфортной жизни разных необычных форм.
Но внезапно с другой, темной стороны планеты, появился дракон, коренной обитатель планеты. Ему не понравилось вторжение людей, и решил он стереть в пыль все строения.
Он прилетал к домам, раскрывал свою пасть и стрелял страшным красным лучом. И каждая поверхность и каждый объем, которого касался этот луч, разрезался по прямой линии.
Прилетел дракон к пирамиде и разрезал ее. Ахнули люди: верхушка пирамиды съехала, осталась лишь прямоугольная плоскость.
Ахнули люди: верхушка пирамиды съехала, осталась лишь прямоугольная плоскость.
Увидел дракон обычный дом — в форме параллелепипеда, — и снова луч разрезал здание. Осталась вместо крыши дыра в форме четырехугольника.
Долетел змей до памятника того народа: “треугольной” башни. Разрушил и это здание. Раскололось здание на две половинки, а в месте их раскола остались треугольные дыры.
Поняли люди: нет сил это терпеть! Собрали межгалактические войска и победили дракона. А после восстанавливали город и удивлялись: как интересно были разрезаны здания.
Так что же делал дракон? Он разрезал геометрические тела, а на месте их разреза оставались сечения.
Сечение — это изображение фигуры, получающееся при мысленном рассечении предмета секущей плоскостью.
Разумеется, никакой дракон не прилетает и не рассекает наши рисунки в тетради. Все сечения чертятся отдельно, а представляются мысленно.
Заметим, что в многогранниках сечение получается в форме многоугольника, вершины которого лежат на ребрах многогранника, а стороны на гранях.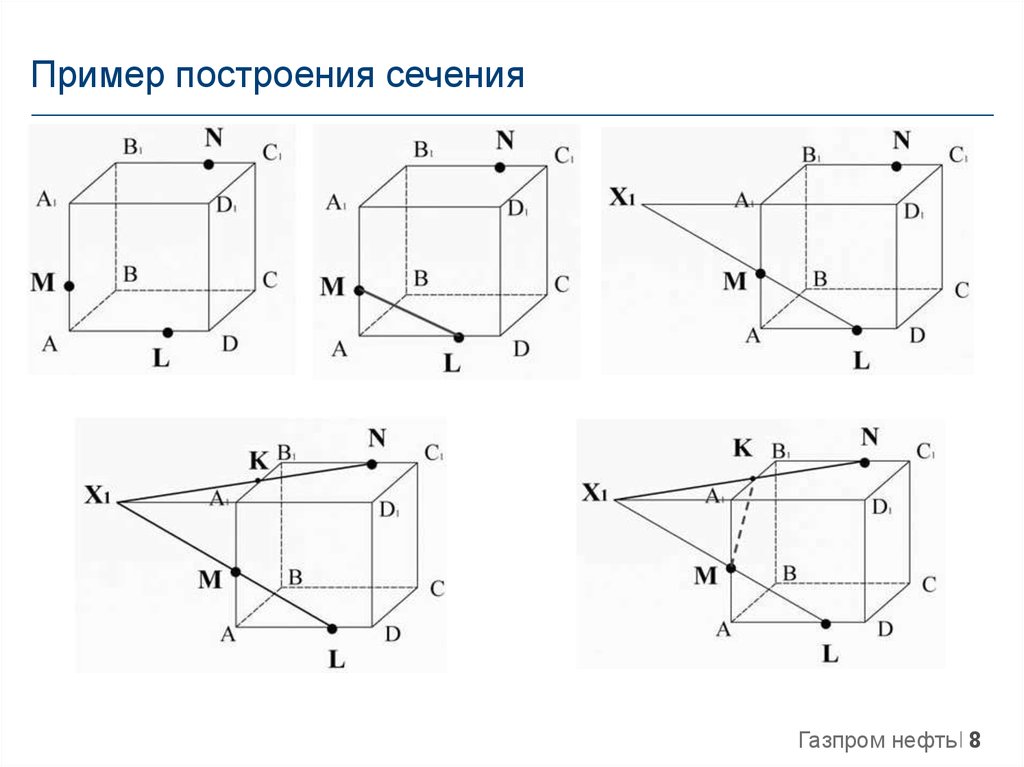 Обратим внимание, что две соседние вершины будут принадлежать одной и той же грани, то есть одной плоскости.
Обратим внимание, что две соседние вершины будут принадлежать одной и той же грани, то есть одной плоскости.
Рассмотрим сечение пирамиды АВС: вершины А, В и С лежат точно на ребрах.
При этом пары вершин А и В, В и С, А и С лежат в одной грани и принадлежат одной плоскости.
Сечение геометрических тел является очень интересным разделом стереометрии. Поскольку это раздел стереометрии, в нем действуют все ее законы, в том числе и аксиомы стереометрии. В этой статье мы не будем заострять на них внимание, прочитать подробнее можно в статье «Аксиомы стереометрии. Расположение прямых и плоскостей в пространстве».
Зачем может потребоваться сечение?
Мы сталкиваемся с ними намного чаще, чем думаем. Они бывают не только в задачах, но и встречаются в жизни.
Что мы делаем, когда нарезаем салат? Рассекаем овощи. Каждый разрез — это сечение.
А что делают архитекторы, когда чертят разрезы? Мысленно рассекают здание и показывают его “внутренности”.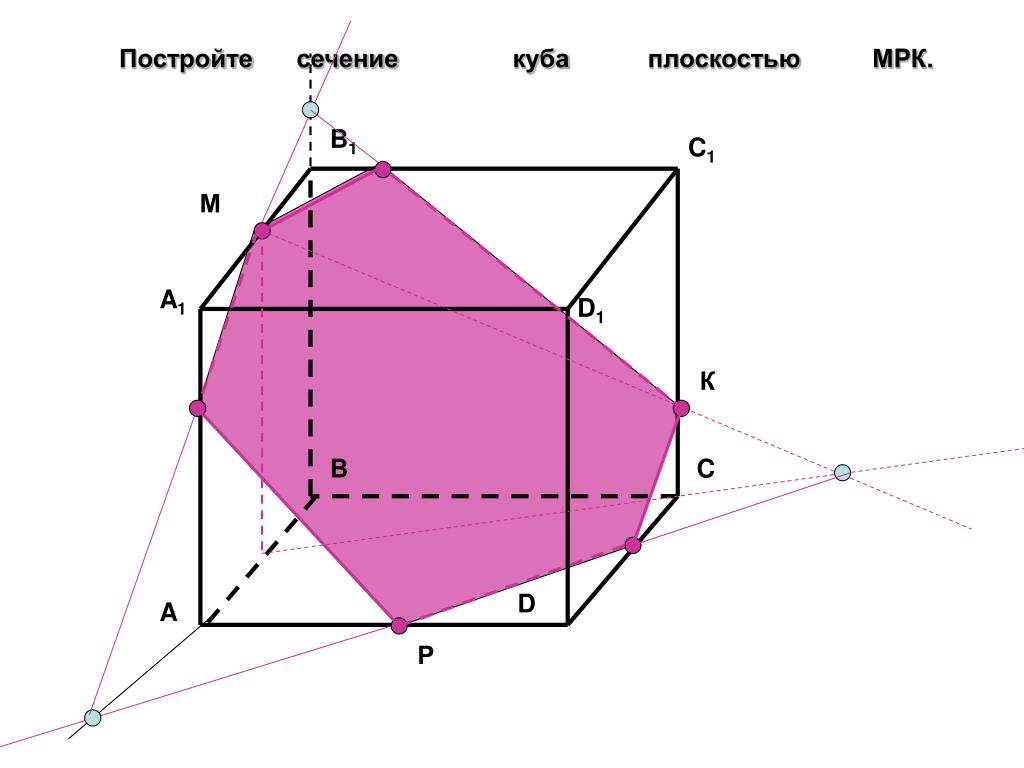
| Чем вода похожа на сечение? Посмотрим на бутылку с водой. Верхний уровень воды можно принять за плоскость, которая рассекает тело бутылки. Наклоняя бутылку и меняя положение воды, можно увидеть различные сечения, которые могут в ней появиться. |
Сечения окружают нас, и в них совсем нет ничего сверхъестественного. А поэтому и разобраться в сечениях в стереометрии не составит для нас труда.
Методы построения сечений
Однако сечения нужно правильно построить. Для их построения существует несколько методов:
- Метод следов;
- Метод внутреннего проектирования;
- Комбинированный метод.
Разберем их по порядку.
Зимой очень интересно гулять по лесу и разглядывать следы животных: вот пробежал заяц, а это, кажется, была маленькая лисица. Здесь просто снег упал с веток дерева.
Все эти тела оставляют след на снегу.
| Что общего у следа на снегу и следа в сечении? Сечение так же, как и любое животное на снегу, оставляет след на гранях многогранника. |
Если мы возьмем карандаш и проведем прямую на листе, он оставит след. Также и плоскость сечения как бы проводит карандашом по граням фигур, оставляя после себя следы.
След плоскости а в плоскости основания многогранника — прямая, по которой секущая плоскость пересекает плоскость основания многогранника.
Вспомним, что плоскость бесконечна, значит, и след можно продолжать в разные стороны бесконечно.
Однако для построения сечений необходимости бесконечно его продолжать нет: достаточно до пересечения с ребром многогранника или продолжением ребра.
Построим сечение куба, которое проходит через точки К, М и Т, чтобы чуть подробнее разобраться в методе следов.
При построении сечений существует очень важный лайфхак: если точки лежат в одной плоскости (то есть в одной грани), то их можно соединить.
1. Заметим, что в нашем кубе это точки К и Т в плоскости (АВВ1) и точки М и Т в плоскости (ВСС1). Поэтому мы можем их соединить.
2. КТ и МТ в нашем случае — это следы плоскости сечения. Продолжим их за точку К и за точку М. Аналогично продолжим стороны АВ и ВС до тех пор, пока их продолжения не пересекутся со следами.
Пусть продолжения прямых АВ и ТК пересекутся в точке Н, а продолжения прямых ТМ и ВС пересекутся в точке F.
3. Обратим внимание, что точки Н и F лежат на продолжении ребер основания, а значит, лежат в плоскости основания куба. Пользуясь лайфхаком, их можно соединить. Таким образом, получим треугольник, который как бы разрезает наш куб.
4. Однако наше сечение не закончено. Вспомним, что все вершины многоугольника должны лежать на ребрах куба, то есть точки Н и F не подходят. Но на самом деле осталось совсем немного закончить построение.
5. Заметим, что прямая HF пересекает ребра AD, DC, назовем точки этих пересечений как N и L.
А также соединим все точки, которые окажутся в одной плоскости.
6. И вот мы получили сечение. Многоугольник TKNLM — сечение куба.
Итак, основной способ построить сечение методом следов — продолжить след сечения до его пересечения с ребрами многогранника или продолжениями его ребер.
А также пользоваться лайфхаком: точки в одной плоскости можно соединять.
Рассмотрим метод внутреннего проектирования.
Иногда метод следов может не помочь: след будет идти параллельно ребру или пересекаться с его продолжением далеко за пределами листа.
В таких случаях часто используется следующее свойство: параллельные плоскости пересекаются другой плоскостью по параллельным прямым. Подробнее про это свойство можно прочесть в статье «Аксиомы стереометрии. Расположение прямых и плоскостей в пространстве».
Польза этого свойства в том, что если сечение пройдет через параллельные плоскости, то оно пересечет их по параллельным линиям. А значит, зная сторону сечения в одной из этих плоскостей и точку в другой плоскости, мы можем просто параллельно перенести прямую и достроить сторону сечения во второй плоскости.
А значит, зная сторону сечения в одной из этих плоскостей и точку в другой плоскости, мы можем просто параллельно перенести прямую и достроить сторону сечения во второй плоскости.
Но будем разбираться на практике. Построим сечение треугольной призмы, проходящее через точки К, М, Т.
1. Первым делом соединим точки, лежащие в одной плоскости. Это точки К и Т в плоскости (АСС1) и точки Т и М в плоскости (АВС).
2. КТ проходит почти параллельно ребру АА1, следовательно, использовать метод следов не рационально.
3. Теперь посмотрим на плоскости (АВС) и (А1В1С1) — они параллельные. А значит прямую сечения можно параллельно перенести в одну из них.
В плоскости (АВС) лежит прямая ТМ, а в плоскости (А1В1С1) лежит точка К, которая является вершиной сечения. Тогда из точки К в плоскости верхнего основания нам нужно провести прямую, параллельную ТМ до пересечения с ребром призмы. Назовем эту точку Е.
Назовем эту точку Е.
4. А теперь мы можем соединить Е и М, так как они лежат в одной плоскости. Четырехугольник КЕМТ — сечение призмы.
Осталось разобраться, в чем заключается комбинированный метод? Он включает в себя и метод следов, и метод внутреннего проектирования, то есть приемы из каждого метода могут применяться вместе в одной и той же задаче.
Все зависит от удобства решения и его быстроты: там, где невозможно применить метод внутреннего проектирования, можно применить метод следов. А там, где применять метод следов неудобно (или невозможно), можно применить метод внутреннего проектирования.
Примеры построения сечений
Рассмотрим несколько примеров построения сечений в различных фигурах.
Пример 1. В правильном тетраэдре провели апофему АТ, на середине которой отметили точку К. АЕ:ЕС = 1:5. Р — точка на ребре CD. Постройте сечение тетраэдра, проходящее через точки К, Е и Р.
Решение. Подробнее про элементы пирамиды и тетраэдра можно прочесть в статье «Пирамида». Сейчас отметим, что апофема — высота боковой грани правильной пирамиды, проведенная к основанию.
Подробнее про элементы пирамиды и тетраэдра можно прочесть в статье «Пирамида». Сейчас отметим, что апофема — высота боковой грани правильной пирамиды, проведенная к основанию.
1. Начнем решение с того, что соединим точки, лежащие в одной плоскости. Е и Р лежат в плоскости (ACD), значит их можно соединить.
2. Рассмотрим плоскость (АСG). Проведем прямую CG. Точки К и Е лежат в одной плоскости, то есть их также можно соединить.
3. Воспользуемся методом следов и продлим прямые ЕК и CG до их пересечения в точке Т.
4. Теперь точки Т и Р будут лежать в одной плоскости основания, следовательно, их можно соединить. Пусть прямая ТР пересекает ребро BD в точке М.
Тогда точки М и К лежат в одной плоскости (ABD) — их тоже можно соединить.
5. Продлим прямую МК до пересечения с ребром АВ в точке О. Точки О и Е лежат в одной плоскости (АВС), соединим их. Сечением тетраэдра будет четырехугольник ОЕРМ.
Пример 2.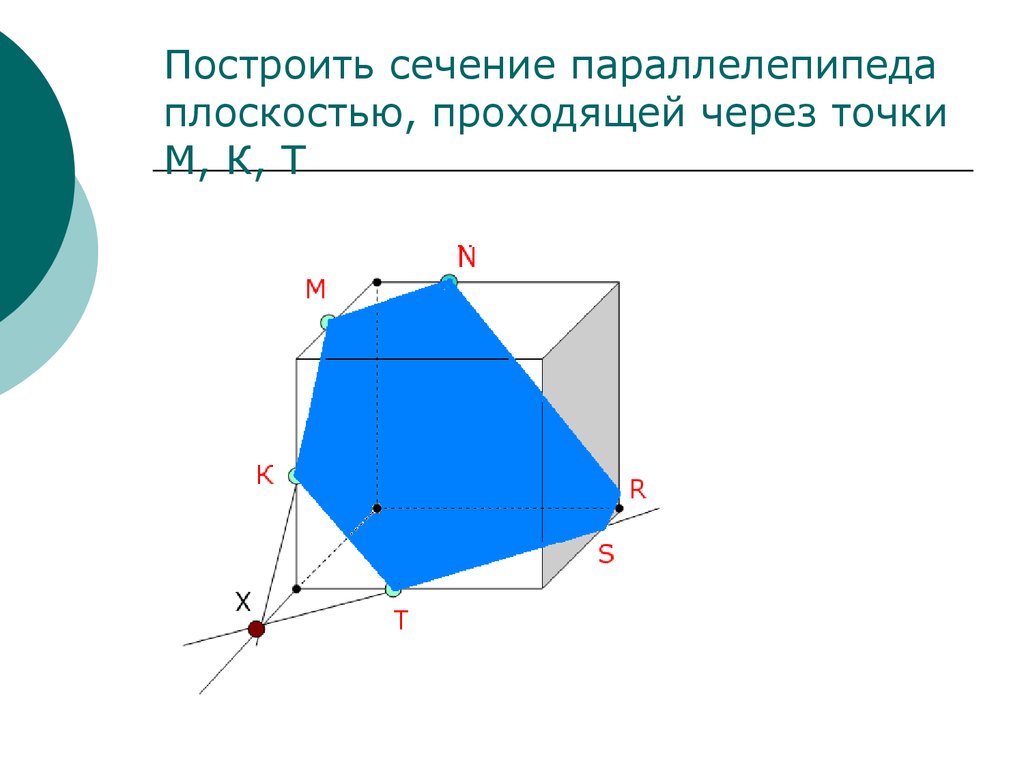 Дана треугольная призма. Постройте сечение призмы, проходящее через точки К, М, Т.
Дана треугольная призма. Постройте сечение призмы, проходящее через точки К, М, Т.
Решение. 1. Соединим точки, лежащие в одной плоскости. Это точки К и Т в плоскости (АСС1).
Воспользуемся методом следов и продолжим прямую ТК до пересечения с продолжением стороны АС в точке Р.
2. Точки Р и М лежат в одной плоскости (АВС), то есть их можно соединить. Пусть прямая РМ пересечет ребро ВС в точке Е.
Воспользуемся методом внутреннего проектирования и проведем из точки Т прямую, параллельную ЕМ. Пусть она пересечет ребро А1В1 в точке О.
3. Осталось соединить точки, лежащие в одной плоскости. Это точки К и Е в плоскости (ВСС1) и точки О и М в плоскости (АВВ1).
Тогда КТОМЕ — сечение призмы.
Пример 3. Дан куб ABCDA1B1C1D1. М — середина ребра АА1. Постройте сечение куба, которое будет параллельно диагонали куба А1С и будет проходить через точки М и В.
Решение. 1. Достроим прямую АС и рассмотрим плоскость (АА1С). Проведем в ней прямую, параллельную А1С из точки М. Пусть она пересечет АС в точке К.
2. Тогда МК — средняя линия треугольник АА1С, значит К — середина АС.
Подробнее про среднюю линию треугольника можно прочесть в статье «Треугольники».
3. Точка К будет принадлежать сечению. Точки В и К лежат в плоскости (АВС) — их можно соединить.
4. В основании куба находится квадрат, его диагонали равны и точкой пересечения делятся пополам.
Подробнее про квадрат и его свойства можно прочитать в статье «Параллелограмм».
Поскольку К — середина диагонали АС, эта же точка будет серединой диагонали BD.
Следовательно, прямую ВК можно продлить до точки D.
5. Осталось только соединить точки, которые лежат в одной плоскости. Это точки М и D в плоскости (ADD1) и точки М и В в плоскости (ABB1).
Тогда сечением будет треугольник DMB.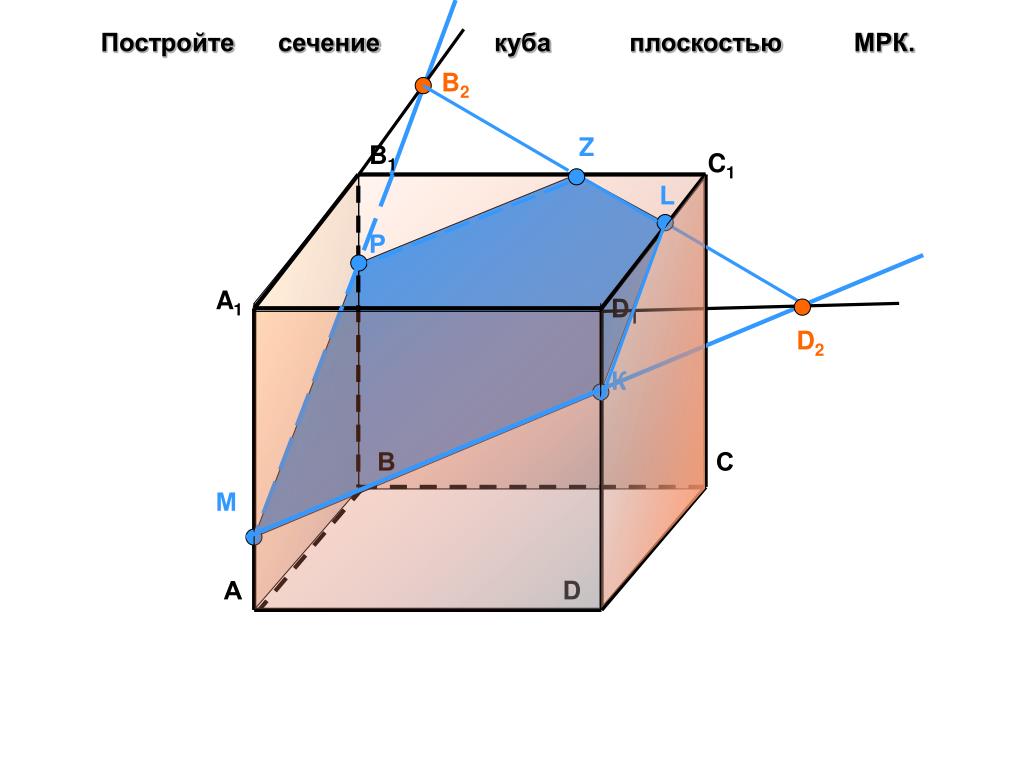
Мы рассмотрели сечения и основные способы их построения. В них нет ничего сложного и стоит помнить, что любое сечение можно представить в реальной жизни. Например, попробовать разрезать пластилиновые фигуры.
Фактчек
- Сечение — это изображение фигуры, получающееся при мысленном рассечении предмета секущей плоскостью. При этом в многогранниках сечения представлены в виде многоугольников, вершины которых лежат на ребрах фигуры.
- Существует несколько методов построения сечения в многогранниках: метод следов, метод внутреннего проектирования и комбинированный метод.
- Метод следов заключается в том, что по следу сечения можно построить его полностью. След сечения — прямая, по которой секущая плоскость пересекает грань многогранника. В методе следов часто нужно продлевать линии и ребра до их пересечения.
- Метод внутреннего проектирования позволяет параллельно переносить сторону сечения в параллельных плоскостях.
 Это может быть удобно в случаях, когда метод следов невозможно или трудно применить.
Это может быть удобно в случаях, когда метод следов невозможно или трудно применить. - Комбинированный метод — метод, который сочетает в себе и метод следов, и метод внутреннего проектирования.
Проверь себя
Задание 1.
Какая форма сечения будет, если треугольную пирамиду разрезать параллельно основанию?
- Треугольник;
- Четырехугольник;
- Шестиугольник;
- Произвольный многоугольник с любым количеством углов.
Задание 2.
Где могут лежать вершины многоугольника, который образовывает сечение?
- Только в вершинах многогранника;
- На ребрах многогранника;
- Только на гранях многогранника;
- В любой точке на многограннике.
Задание 3.
Что такое след сечения?
- Продолжения сторон сечения;
- Вершины многоугольника, который образовывает сечение;
- Прямая, по которой секущая плоскость пересекает плоскость основания многогранника;
- Все вышеперечисленные варианты.

Задание 4.
Что можно сделать с точками, которые лежат на одной грани?
- Соединить;
- Ни в коем случае нельзя их соединять;
- Построить сечение, опираясь на две разные стороны, не соединяя стороны;
- Ни один из перечисленных вариантов.
Задание 5.
Как можно воспользоваться методом внутреннего проектирования?
- Произвольно переносить линии сечения в любых гранях;
- Произвольно переносить линии сечения в параллельных гранях;
- Перпендикулярно переносить линии сечения в перпендикулярных гранях;
- Параллельно переносить линии сечения в параллельных гранях.
Ответы: 1. — 1 2. — 2 3. — 3 4. — 1 5. — 4
построить сечение пирамиды
Разберем, как построить сечение пирамиды, на конкретных примерах. Поскольку в пирамиде нет параллельных плоскостей, построение линии пересечения (следа) секущей плоскости с плоскостью грани чаще всего предполагает проведение прямой через две точки, лежащие в плоскости этой грани.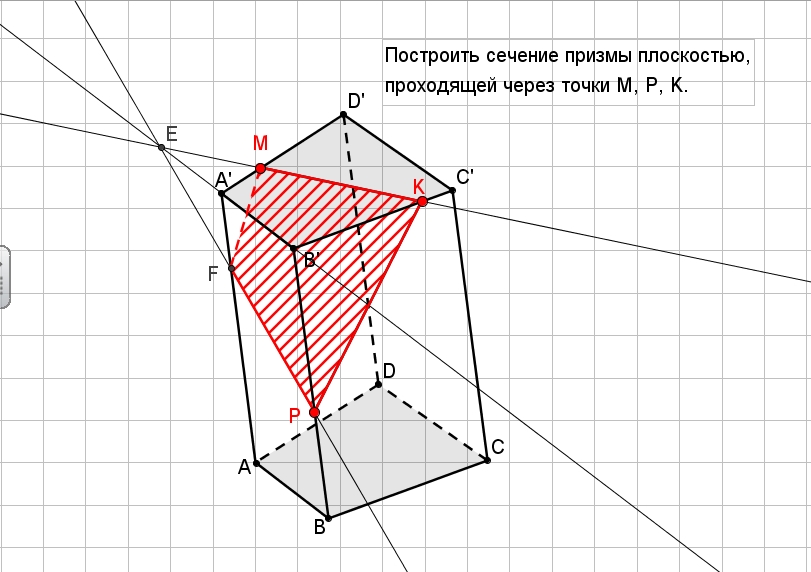
В простейших задачах требуется построить сечение пирамиды плоскостью, проходящей через данные точки, уже лежащие в одной грани.
Пример.
Построить сечение плоскостью (MNP)
Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.
Треугольник MNP — сечение пирамиды
Точки M и N лежат в одной плоскости ABS, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он видимый, значит, соединяем M и N сплошной линией.
Точки M и P лежат в одной плоскости ACS, поэтому через них проведем прямую. След — отрезок MP. Мы его не видим, поэтому отрезок MP проводим штрихом. Аналогично строим след PN.
Треугольник MNP — искомое сечение.
Если точка, через которую требуется провести сечение, лежит не на ребре, а на грани, то она не будет концом следа-отрезка.
Пример. Построить сечение пирамиды плоскостью, проходящей через точки B, M и N, где точки M и N принадлежат, соответственно, граням ABS и BCS.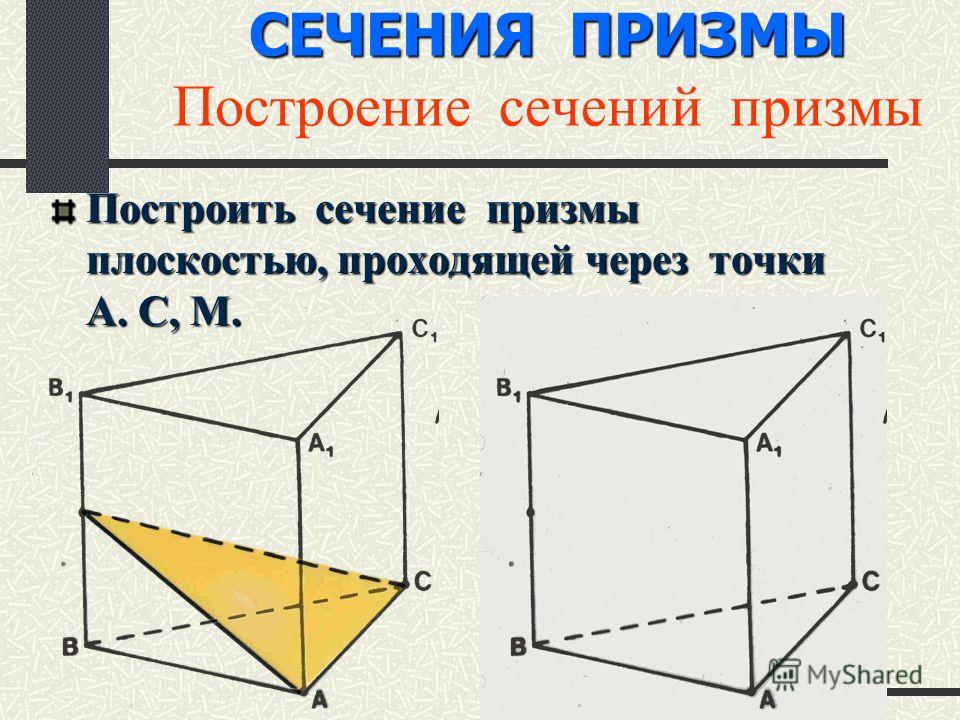
Здесь точки B и M лежат в одной грани ABS, поэтому можем через них провести прямую.
Аналогично проводим прямую через точки B и P. Получили, соответственно, следы BK и BL.
Точки K и L лежат в одной грани ACS, поэтому через них можем провести прямую. Ее след — отрезок KL.
Треугольник BKL — искомое сечение.
Однако не всегда через данные в условии точки удается провести прямую. В этом случае нужно найти точку, лежащую на прямой пересечения плоскостей, содержащих грани.
Пример. Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.
Точки M и N лежат в одной плоскость ABS, поэтому через них можно провести прямую. Получаем след MN. Аналогично — NP. Оба следа видимые, поэтому соединяем их сплошной линией.
Точки M и P лежат в разных плоскостях. Поэтому соединить их прямой не можем.
Продолжим прямую NP.
Она лежит в плоскости грани BCS.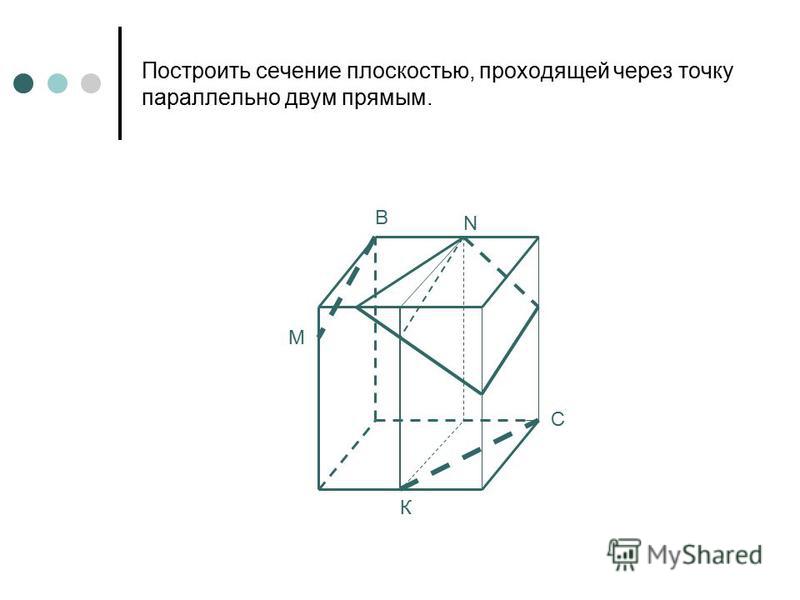 NP пересекается только с прямыми, лежащими в этой же плоскости. Таких прямых у нас три: BS, CS и BC. С прямыми BS и CS уже есть точки пересечения — это как раз N и P. Значит, ищем пересечение NP с прямой BC.
NP пересекается только с прямыми, лежащими в этой же плоскости. Таких прямых у нас три: BS, CS и BC. С прямыми BS и CS уже есть точки пересечения — это как раз N и P. Значит, ищем пересечение NP с прямой BC.
Точку пересечения (назовем ее H), получаем, продолжая прямые NP и BC до пересечения.
Эта точка H принадлежит как плоскости (BCS), поскольку лежит на прямой NP, так и плоскости (ABC), поскольку лежит на прямой BC.
Таким образом мы получили еще одну точку секущей плоскости, лежащей в плоскости (ABC).
Через H и точку M, лежащую в этой же плоскости, можем провести прямую.
Получим след MT.
T — точка пересечения прямых MH и AC.
Так как T принадлежит прямой AC, то через нее и точку P можем провести прямую, так как они обе лежат в одной плоскости (ACS).
4-угольник MNPT — искомое сечение пирамиды плоскостью, проходящей через данные точки M,N,P.
Мы работали с прямой NP, продлевая ее для отыскания точки пересечения секущей плоскости с плоскостью (ABC).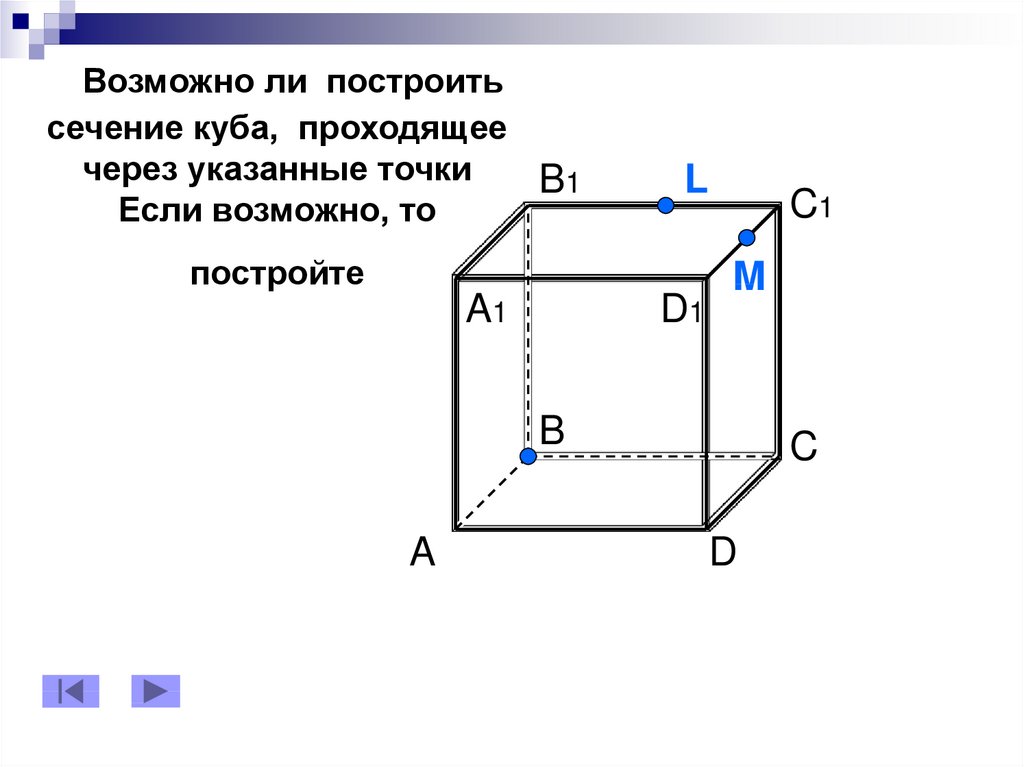 Если работать с прямой MN, приходим к тому же результату.
Если работать с прямой MN, приходим к тому же результату.
Рассуждаем так: прямая MN лежит в плоскости (ABS), поэтому пересекаться может только с прямыми, лежащими в этой же плоскости. У нас таких прямых три: AB, BS и AS. Но с прямыми AB и BS уже есть точки пересечения: M и N.
Значит, продлевая MN, ищем точку пересечения ее с прямой AS. Назовем эту точку R.
Точка R лежит на прямой AS, значит, она лежит и в плоскости (ACS), которой принадлежит прямая AS.
Поскольку точка P лежит в плоскости (ACS), через R и P можем провести прямую. Получаем след PT.
Точка T лежит в плоскости (ABC), поэтому через нее и точку M можем провести прямую.
Таким образом, получили все то же сечение MNPT.
Рассмотрим еще один пример такого рода.
Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.
Через точки M и N, лежащие в одной плоскости (BCS), проводим прямую. Получаем след MN (видимый).
Получаем след MN (видимый).
Через точки N и P, лежащие в одной плоскости (ACS), проводим прямую. Получаем след PN (невидимый).
Через точки M и P прямую провести не можем.
1) Прямая MN лежит в плоскости (BCS), где есть еще три прямые: BC, SC и SB. С прямыми SB и SC уже есть точки пересечения: M и N. Поэтому ищем точку пересечения MN с BC. Продолжив эти прямые, получаем точку L.
Точка L принадлежит прямой BC, а значит, она лежит в плоскости (ABC). Поэтому через L и P, которая также лежит в плоскости (ABC) можем провести прямую. Ее след — PF.
F лежит на прямой AB, а значит, и в плоскости (ABS). Поэтому через F и точку M, которая также лежит в плоскости (ABS), проводим прямую. Ее след — FM. Четырехугольник MNPF — искомое сечение.
2) Другой путь — продолжить прямую PN. Она лежит в плоскости (ACS) и пересекается с прямыми AC и CS, лежащими в этой плоскости, в точках P и N.
Значит, ищем точку пересечения PN с третьей прямой этой плоскости — с AS.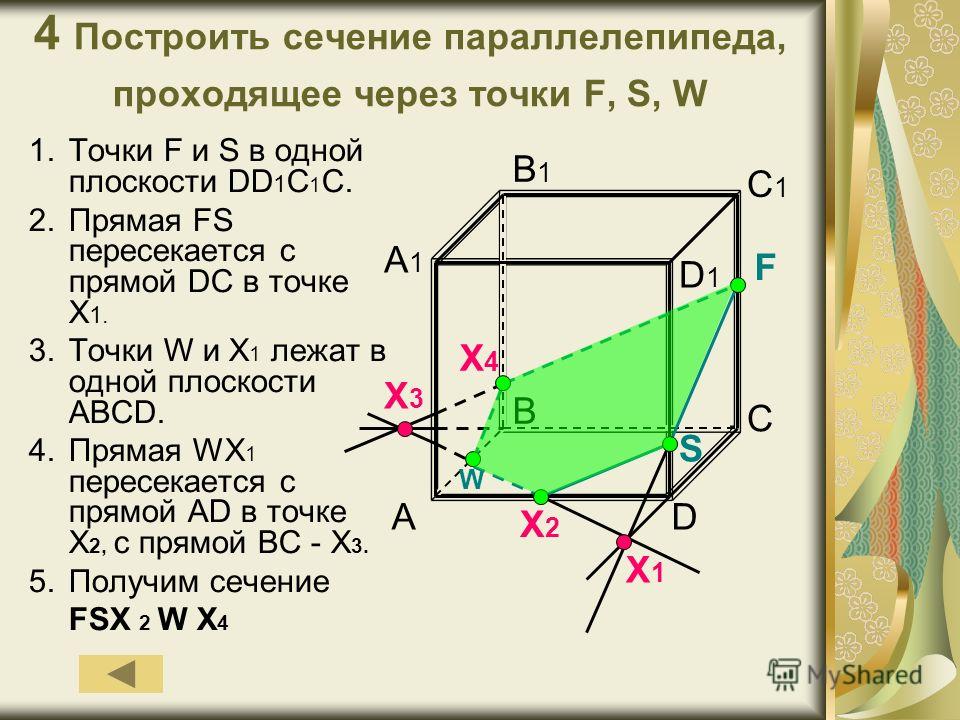 Продолжаем AS и PN, на пересечении получаем точку E. Поскольку точка E лежит на прямой AS, принадлежащей плоскости (ABS), то через E и точку M, которая также лежит в (ABS), можем провести прямую. Ее след — FM. Точки P и F лежат водной плоскости (ABC), проводим через них прямую и получаем след PF (невидимый).
Продолжаем AS и PN, на пересечении получаем точку E. Поскольку точка E лежит на прямой AS, принадлежащей плоскости (ABS), то через E и точку M, которая также лежит в (ABS), можем провести прямую. Ее след — FM. Точки P и F лежат водной плоскости (ABC), проводим через них прямую и получаем след PF (невидимый).
Типы чертежей в разрезе — Строительные чертежи
Последнее обновление: сб, 13 августа 2022 г. |
Строительные чертежи
Можно рисовать сечения всего здания, внутреннего пространства или объекта. Они называются полными разделами. Однако, если необходимо проиллюстрировать только изолированную область, можно также нарисовать частичный разрез. Разделы могут быть вырезаны различными способами для отображения более подробной информации. Секция может проходить через все здание (так называемая секция здания) или только через стену (секция стены).
Могут потребоваться оба варианта, потому что небольшой размер и сложность участка здания обычно означает, что материалы и детали, связанные со стенами, не могут быть нарисованы там.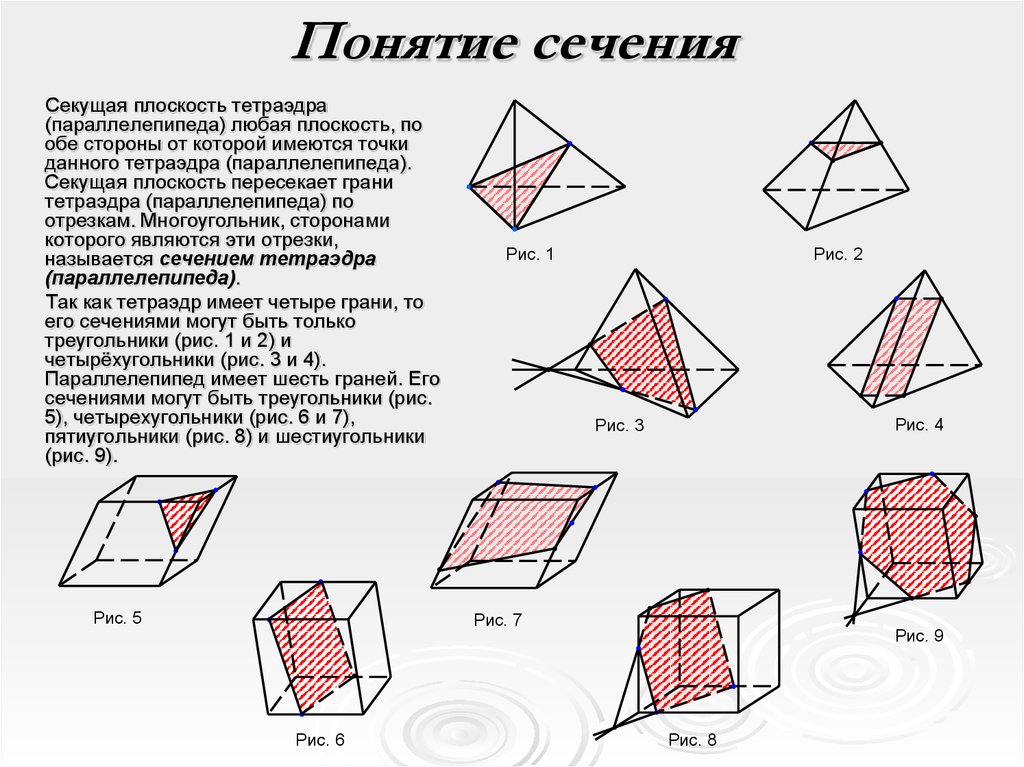 Символ на участке здания, показанный на рис. 8-4, отмечает площадь стены, которую необходимо увеличить. Сечение стены (рис. 8-5) нарисовано так, чтобы точно показать множество деталей и материалов, необходимых для сборки.
Символ на участке здания, показанный на рис. 8-4, отмечает площадь стены, которую необходимо увеличить. Сечение стены (рис. 8-5) нарисовано так, чтобы точно показать множество деталей и материалов, необходимых для сборки.
фин. напольный плавник. нижний пол
ДЕРЕВЯННЫЕ ДОМА
1/16′ OBS. ОБШИВКА ЛОХА
Изоляция r-40
ДЕРЕВЯННЫЕ ДОМА
1/16′ OBS. ОБШИВКА GOOF
r-40 изоляционное ребро. напольный плавник. louer floor
/2″ Ceiuns Chase
Рис. 8-6 В увеличенном разрезе может быть показана только часть сборки здания для изображения конкретных деталей, таких как конструкция встроенного шкафа.
/2″ Ceiuns Chase
СТЕНА СЕКЦИЯ
Рис. 8-5 Это увеличенная секция стены, обозначенная ключом на секции здания на Рис. 8-4.
Рис. 8-6 В увеличенном разрезе может быть показана только часть сборки здания для отображения конкретных деталей, таких как конструкция встроенного шкафа.
ВЕРХНЯЯ ПЕРЕГОРОДКА
дверцы шкафа окрашены в черный цвет —
2 регулируемые полки ■ 3/4′ блокировка из МДФ с отделкой drtujall
СЕКЦИЯ ШКАФА
ПЕРЕГОРОДКА ВВЕРХУ
2 0 9 дверцы шкафа — регулируемые полки в черный цвет ■ 3/4 фута из МДФ, блокирующий бетон и обработанную поверхность с отделкой drtuja, нижняя сторона шкафа, чтобы соответствовать вертикальным поверхностям, полная задняя панель
3/4 дюйма из МДФ с 1-1/2 футовым выступом ящика шкафа с аккуридом (ИЛИ равные/скользящие
3-футовые проволочные тяги из нержавеющей стали – тип.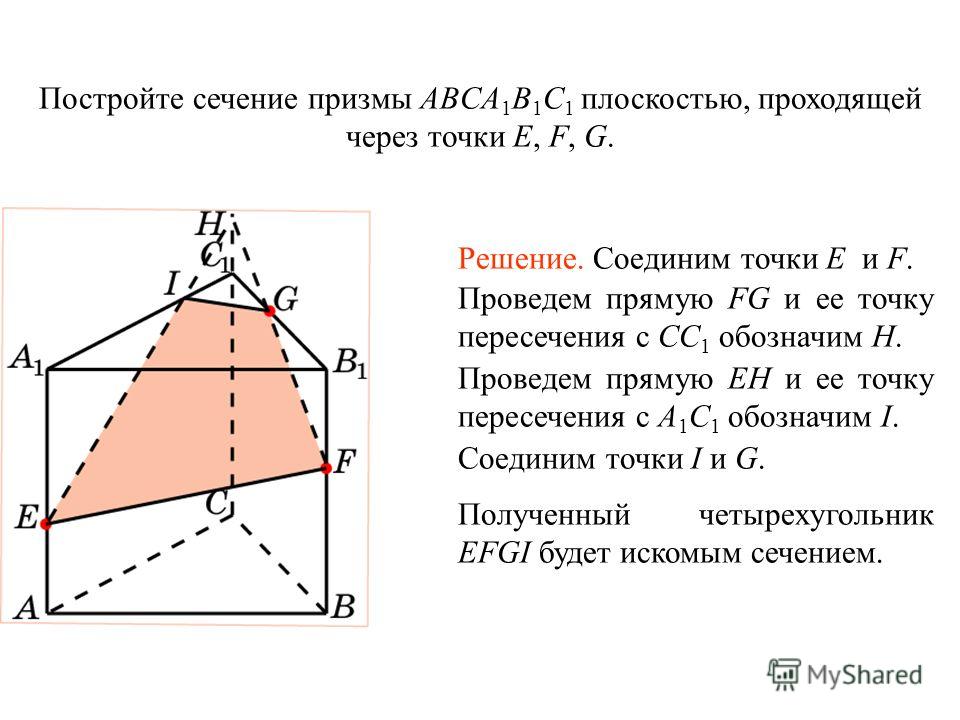 • нижний ящик « шкафчик регулируемая полка f3/4′ мдф; на системе штифтовых отверстий — с шагом 1/4 дюйма с хромированными опорами для полок дверцы шкафа — 3/4 дюйма из МДФ и отбойным основанием
• нижний ящик « шкафчик регулируемая полка f3/4′ мдф; на системе штифтовых отверстий — с шагом 1/4 дюйма с хромированными опорами для полок дверцы шкафа — 3/4 дюйма из МДФ и отбойным основанием
встроенные или нестандартные компоненты в помещении, такие как стеллажи, стойки регистрации, комоды, бары, витрины, шкафы и прилавки. На рисунке 8-6 показана секция встроенного шкафа. Эти типы секций обсуждаются более подробно. в главе 9.
СЕКЦИЯ ШКАФА
В чертежах внутренней конструкции иногда термины «сечение» и «деталь» меняются местами, что вызывает некоторую путаницу. Например, разрезы в разрезе небольших частей конструкции или объектов часто называют деталями. Но детали не всегда рисуются в разрезе. Они также могут включать увеличенные части плана этажа или фасада.
Масштаб чертежей в разрезе может варьироваться от y%» до 3″ (от 3,17 мм до 76 мм) в зависимости от размера чертежной бумаги, размера здания (или компонента) и желаемых характеристик, которые должны быть показаны . Конкретная информация, отображаемая в разделе, может различаться в зависимости от того, является ли он проектным или строительным чертежом. Строительные чертежи показывают только те элементы или компоненты помещения, которые встроены или прикреплены к конструкции. Передвижная мебель не показана на этом типе чертежа.
Конкретная информация, отображаемая в разделе, может различаться в зависимости от того, является ли он проектным или строительным чертежом. Строительные чертежи показывают только те элементы или компоненты помещения, которые встроены или прикреплены к конструкции. Передвижная мебель не показана на этом типе чертежа.
Продолжить чтение здесь: Строительные секции
Была ли эта статья полезной?
Как создать свой первый раздел темы Shopify — Разработка темы Shopify (2022)
Предоставление вашим клиентам творческого контроля является ключевым моментом, особенно когда они хотят иметь возможность настраивать витрину своего магазина. Функция разделов Shopify — это мощный инструмент для персонализации тем Shopify, поэтому их эффективное использование и соблюдение рекомендаций откроют ряд возможностей для ваших клиентов.
Если вы создаете тему Shopify с нуля или настраиваете тему для клиента, вам нужно создать несколько разных типов разделов, которые будут различаться в зависимости от контекста. Кроме того, клиенты ожидают удобного и интуитивно понятного интерфейса, а это означает, что правильный раздел в нужном месте может оказать огромное влияние на конверсию.
Кроме того, клиенты ожидают удобного и интуитивно понятного интерфейса, а это означает, что правильный раздел в нужном месте может оказать огромное влияние на конверсию.
В этой статье мы расскажем, как начать создавать тематические разделы различных типов и правила их использования, чтобы вы могли помочь своим клиентам настроить свой магазин. Мы также рассмотрим некоторые примеры конкретных разделов из нашей темы Dawn, доступной в исходном коде, чтобы продемонстрировать, как именно вы можете использовать их в реальных сценариях.
Что такое тематические разделы?
На высоком уровне разделы представляют собой модульные компоненты темы Shopify, которые продавцы могут настраивать. Разделы содержат контент и настройки для определенных областей магазина Shopify, таких как основные элементы страницы продукта или компонент слайд-шоу.
В этих разделах разработчики имеют доступ к целому ряду различных типов настроек, от ввода текста и средств выбора изображений до пользовательского HTML и меню, которые продавцы могут настраивать в редакторе тем и заполнять своим содержимым.
Разделы содержатся в каталоге /sections темы и могут быть статически включены в файлы макета темы (например, верхний и нижний колонтитулы) или динамически добавляться в любой шаблон из редактора тем. Чтобы получить представление о различных компонентах, которые могут быть представлены в виде разделов, вы можете изучить каталог /sections темы Dawn.
С запуском Интернет-магазина 2.0 разделы теперь можно использовать в качестве основного способа организации всех различных аспектов вашей темы, от целых страниц до отдельных элементов. Как мы расскажем в этой статье, возможность добавлять разделы в любые шаблоны JSON позволит вам легко упорядочивать разные страницы, которые можно дополнительно улучшить, когда продавцы настроят свою тему.
Шаблоны и разделы
Одной из предпосылок для изучения того, как работают разделы в темах Shopify, является понимание системы шаблонов тем Shopify. В Online Store 2.0 каждый тип страницы может быть представлен в виде файла . в каталоге  json
json /templates темы. Разработчики могут структурировать каждый тип страницы, определяя, какие разделы будут отображаться по умолчанию в этих файлах шаблонов JSON.
Эти шаблоны JSON не содержат никакой разметки или объектов Liquid для отображения содержимого магазина. Это просто файлы данных, указывающие, какие разделы будут отображаться на странице по умолчанию и в каком порядке.
Базовый пример того, как может выглядеть файл шаблона product.json : раздел появляется по умолчанию. Когда продавец настраивает эту страницу и добавляет на нее дополнительные разделы, файл шаблона product.json будет обновлен с учетом этой информации. Мы подробнее рассмотрим этот процесс в этой статье, когда рассмотрим, как разделы включаются в шаблоны.
Основы разделов
При разработке темы с использованием разделов и шаблонов JSON вы можете рассмотреть возможность создания файлов разделов в двух разных категориях: «основные» разделы страницы и отдельные модульные компоненты.
Разделы главной страницы
В разделе главной страницы вы должны включить все содержимое по умолчанию для этой страницы. Например, в основной раздел страницы продукта вы должны включить важные элементы для отображения продукта и связанных с ним свойств, таких как название продукта, описание, медиа, цена и форма добавления в корзину.
Вы можете получить доступ к переменным или объектам Liquid в разделе в зависимости от того, в какой шаблон страницы включен раздел. Это означает, что раздел, который будет отображаться в шаблоне product.json , сможет получить доступ к любым атрибутам. объекта product Liquid, представляющего продукт, страница которого отображается.
Аналогичным образом раздел, включенный в файл collection.json , сможет получить доступ ко всем атрибутам коллекция Жидкий объект. Все разделы, независимо от того, где они появляются, могут получить доступ к любому из глобальных объектов Liquid.
В дополнение к разметке и специфичным для страницы объектам Liquid, которые вы будете добавлять в раздел главной страницы, вы также можете создавать настройки в тегах {% schema %} . Эти настройки могут ссылаться на элементы раздела и могут быть изменены продавцами в редакторе тем.
Поскольку раздел главной страницы содержит разметку, специфичную для одного типа страницы, вам нужно включить ее только в связанный с ней шаблон. Чтобы предотвратить добавление раздела главной страницы к другим типам страниц из редактора темы, он не должен содержать предустановки в своей схеме раздела.
Чтобы просмотреть пример раздела главной страницы, вы можете изучить файл main-product.liquid в каталоге /sections Dawn или любой из разделов с префиксом main в заголовке. Как правило, вы также должны называть разделы главной страницы с помощью main в заголовке, чтобы вы могли различать разные типы разделов.
Модульные разделы
Модульные разделы — это разделы, которые можно многократно использовать в разных разделах интернет-магазина и дополнять основные элементы страницы.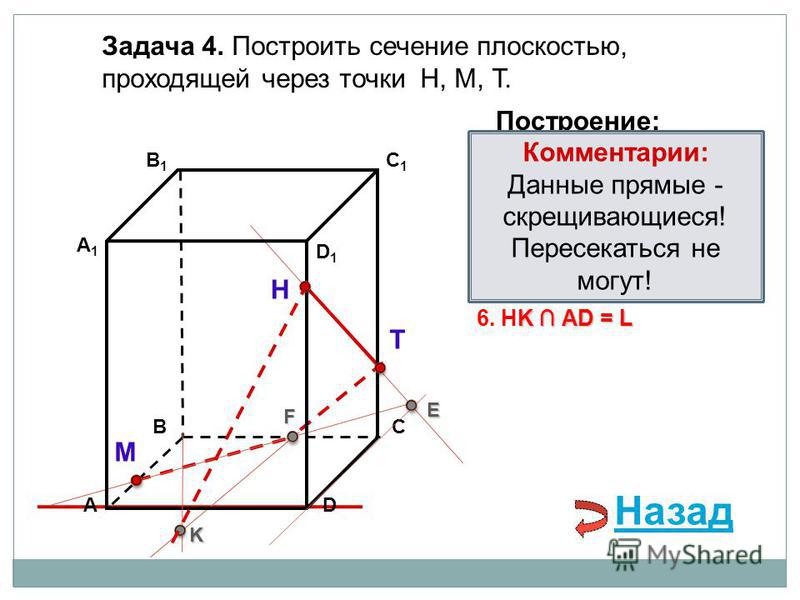 Примеры этих типов разделов включают избранные коллекции, слайд-шоу и формы подписки на рассылку новостей.
Примеры этих типов разделов включают избранные коллекции, слайд-шоу и формы подписки на рассылку новостей.
Обычно эти разделы добавляются на страницы продавцами с помощью редактора тем, а не добавляются по умолчанию в шаблон страницы. Чтобы раздел можно было добавить на страницу через редактор, раздел должен содержать пресеты в своей схеме. После добавления этих пресетов раздел будет доступен, когда продавец нажмет Добавить раздел в редакторе тем.
В отличие от «основных» разделов страницы, модульные разделы обычно содержат контент и разметку, которые можно повторно использовать на разных типах страниц и в разных контекстах в магазине Shopify. Поэтому разработчикам следует избегать полагаться на специфичные для страницы объекты Liquid в этих разделах.
Однако можно ограничить доступ к разделу только на определенных типах страниц, используя атрибут templates в схеме раздела. Например, если вы хотите ограничить раздел только страницами продуктов и коллекций, вы должны включить эту строку в теги схемы раздела :
"шаблоны": ["продукт", "коллекция"]
Атрибут templates принимает список строк, представляющих тип страницы.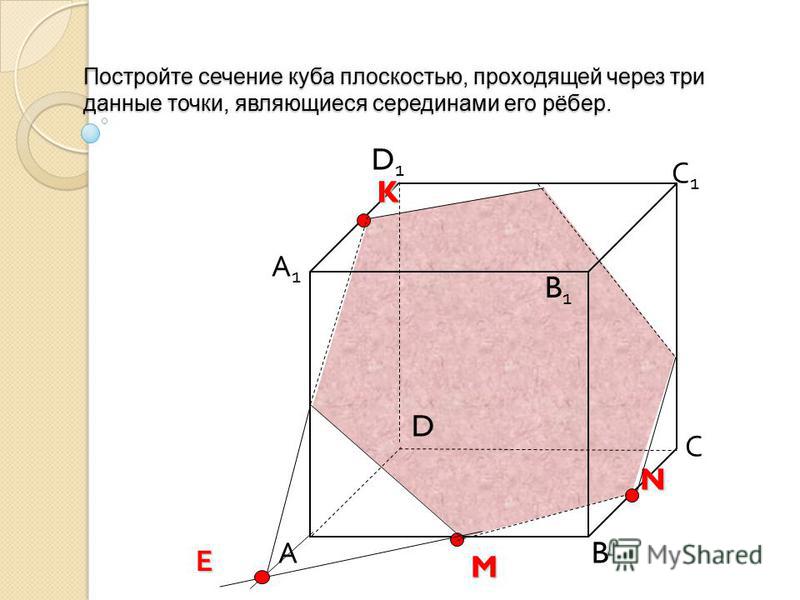
В зависимости от того, какую функциональность вы хотите включить в свою тему, или от конкретных требований вашего клиента, вы, вероятно, создадите ряд различных разделов, обеспечивающих уникальные функции. Чтобы просмотреть примеры модульных разделов, вы можете изучить раздел информационного бюллетеня или раздел расширенного текста, используемый в Dawn.
Настройки раздела
Мы кратко рассмотрели, как можно использовать настройки файла раздела для создания параметров настройки, к которым могут получить доступ продавцы, но давайте углубимся в них немного глубже, чтобы увидеть, как они устроены.
Как мы видели, настройки включены в файлы разделов, внутри тегов {% schema %} , которые обозначают, что эти настройки должны отображаться в пользовательском интерфейсе редактора тем. Очень простой пример этого можно увидеть с пользовательским текстовым разделом, который может выглядеть примерно так:
В этом примере у нас есть два элемента HTML: элемент заголовка и элемент абзаца. Каждый из этих элементов содержит динамическое содержимое, которое мы создали с помощью раздела
Каждый из этих элементов содержит динамическое содержимое, которое мы создали с помощью раздела . Настройки Жидкий объект. Этот объект раздела позволяет нам получать значения настроек, ссылаясь на уникальный идентификатор настройки.
Под разметкой HTML и Liquid у нас есть настройки нашего раздела, содержащиеся в наших тегах {% schema %} . Каждая настройка представлена объектом, где мы можем определить настройку id , ее тип и то, как она будет отображаться в редакторе. Чтобы получить доступ к настройке раздела в Liquid, добавьте его идентификатор к объекту жидкости section.settings . Мы также определяем тип настройки и то, как она будет отображаться в редакторе тем.
В настройках наших тегов схемы:
-
idотносится к определяемой переменной Liquid -
типопределяет тип вывода, который мы создаем -
меткаобеспечивает контекст, отображаемый в редакторе темы -
по умолчаниюназначает значение по умолчанию
В этом примере я создал текстовый блок для нашего заголовка и блок RichText для основного текста, но вы можете добавить широкий спектр типов вывода в зависимости от требований вашего клиента.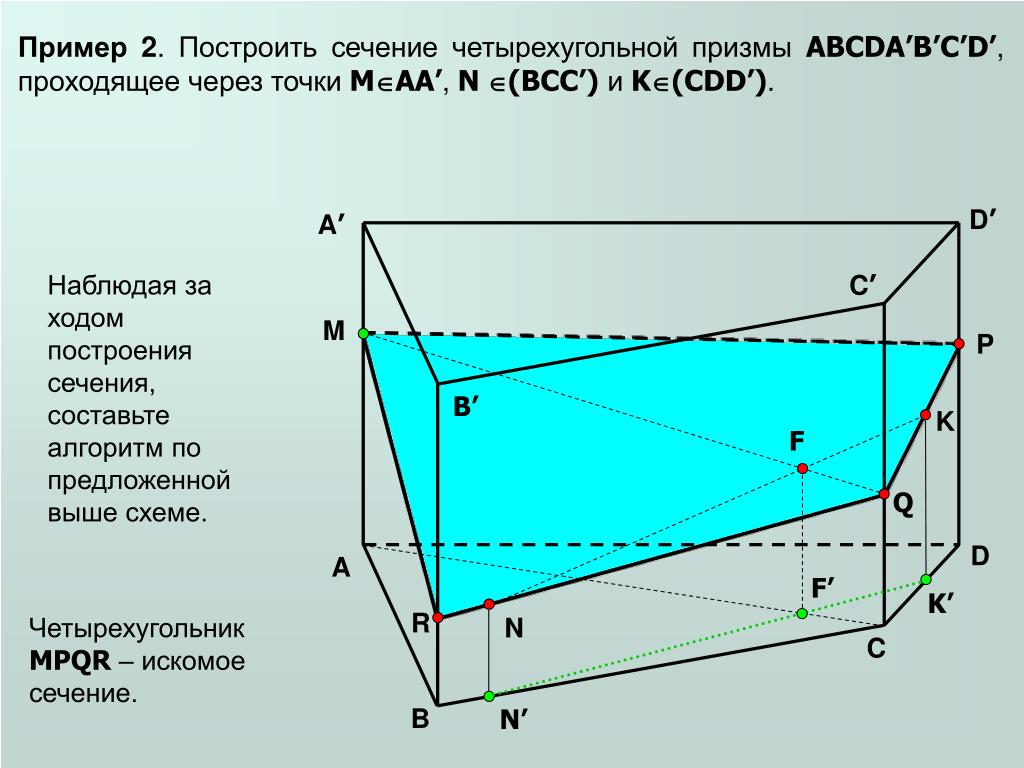 Другие допустимые типы ввода включают
Другие допустимые типы ввода включают image_picker , радио , video_url и font_picker .
Этот пример теперь является допустимым разделом, однако нам не хватает одного ключевого аспекта: определения, где именно раздел появится в теме. Позже мы рассмотрим несколько различных подходов к включению разделов, но сейчас мы позволим добавить раздел через редактор темы на любую страницу, создав пресеты в разделе.
Предустановки являются конфигурациями разделов по умолчанию и добавляются в 9 разделов.0079 {% схема %} тегов. В нашем простом примере пресеты могут выглядеть так:
"пресеты": [
{
"имя": "пользовательский текст",
"категория": "Пользовательский"
}
]
После добавления в наш пример настраиваемый раздел текстового поля будет выглядеть так:
Теперь, если мы перейдем к редактору темы и выберем Добавить раздел на любой странице, этот раздел появится в качестве доступной опции. Созданные нами настройки раздела появятся на правой боковой панели с добавленными нами метками и текстом по умолчанию, и мы можем заполнить параметры ввода текста, которые будут отображаться в нашем разделе.
Созданные нами настройки раздела появятся на правой боковой панели с добавленными нами метками и текстом по умолчанию, и мы можем заполнить параметры ввода текста, которые будут отображаться в нашем разделе.
Это простой пример, показывающий взаимосвязь между настройками раздела и переменными, которые вы можете создавать в разделах, а также то, как они отображаются в редакторе тем. Для более продвинутой модели вы можете изучить раздел расширенного текста темы Dawn.
Включение разделов на страницы
Как мы уже упоминали, существует несколько способов включения разделов на страницы темы. Давайте рассмотрим каждый из этих подходов по отдельности и раскроем некоторые применимые к ним правила.
1. Включение разделов в шаблоны JSON
Когда мы рассмотрели разделы главной страницы, мы увидели, что файлы шаблонов JSON принимают свойство «main» , которое становится разделом по умолчанию для этого типа страницы и должно включать все важные элементы контента для этой страницы.
В дополнение к «основному» разделу также можно включить другие разделы в шаблон JSON, которые будут отображаться по умолчанию на страницах этого типа. Если мы используем шаблон продукта JSON в качестве примера, мы могли бы включить раздел рекомендаций продукта на страницу, добавив новый объект ниже "main" section:
В этом случае мы присваиваем имя разделу, рекомендации , а свойство type используется для определения того, какой файл в каталоге /sections мы хотим включить.
Поскольку этот шаблон JSON ссылается более чем на один раздел, нам нужно определить, как разделы отображаются последовательно в объекте порядка . Каждому разделу, включенному в шаблон JSON, необходимо будет назначить порядок по умолчанию, однако продавцы могут изменить порядок разделов в редакторе тем.
Разделы без пресетов, добавленные в шаблоны JSON, нельзя удалить в редакторе тем, но их можно скрыть, если они не требуются продавцу.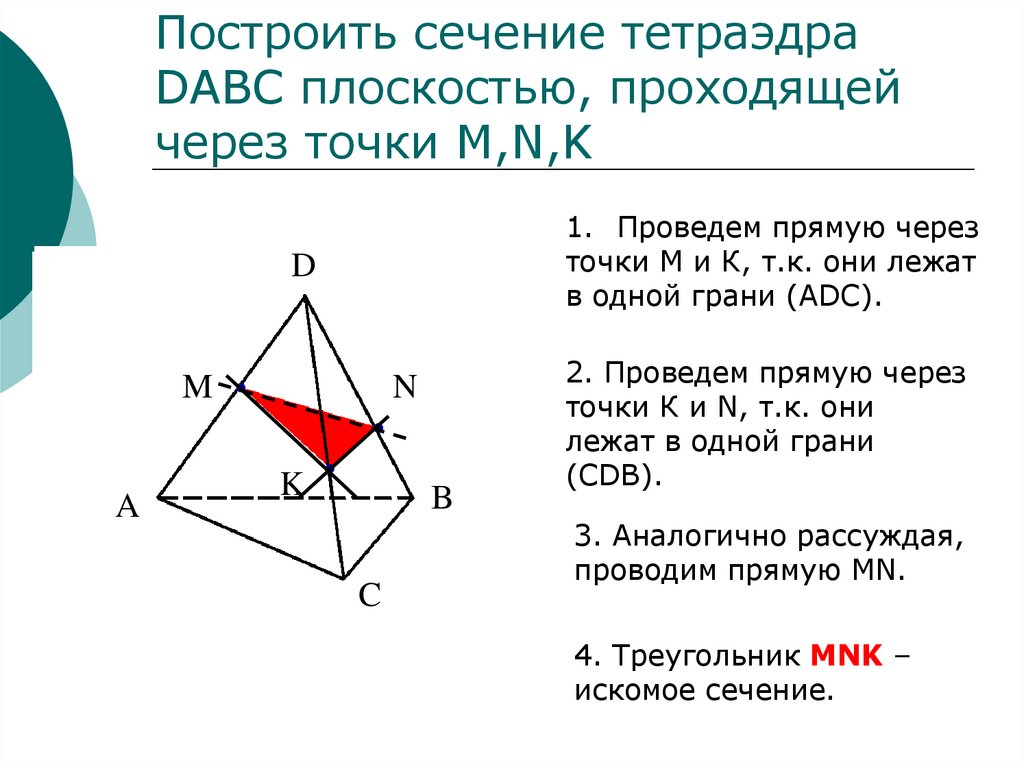 Чтобы увидеть реальный пример того, как разделы могут быть организованы в шаблоне JSON, вы можете изучить шаблон продукта Dawn.
Чтобы увидеть реальный пример того, как разделы могут быть организованы в шаблоне JSON, вы можете изучить шаблон продукта Dawn.
2. Включение разделов в качестве опций на всех страницах
Как мы видели с нашим пользовательским текстом, можно сделать раздел доступным на всех страницах темы, когда пресетов присутствуют в схема настройки.
«предустановки»: [
{
«имя»: «пользовательский текст»,
«категория»: «пользовательский»
}
]
При использовании этого подхода эти разделы можно добавлять, перемещать и удалять из редактора тем. Эти разделы также могут быть ограничены определенными страницами с помощью свойства шаблонов .
Эта функция перетаскивания означает, что при создании пользовательских динамических разделов будет разблокирован широкий спектр параметров для персонализации магазинов. Вы можете создавать подвижные разделы для видео, продуктов или галерей изображений. Хорошим примером раздела, использующего этот метод, может быть раздел информационного бюллетеня Dawn.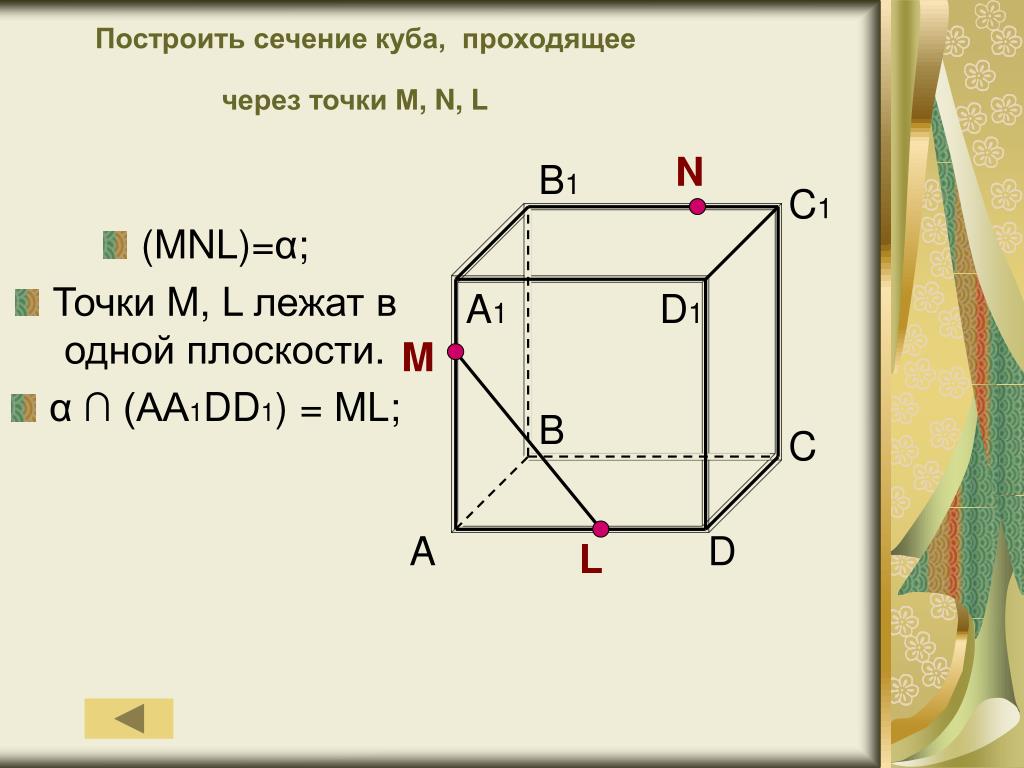
3. Использование тегов {% section %} для добавления статических разделов
Тег Liquid section позволяет визуализировать раздел из каталога /sections в файле макета или шаблона Liquid. Этот тег может выглядеть так:
{% section 'header' %}
Разделы, добавленные с помощью этого тега section , нельзя удалить, переместить или скрыть в редакторе тем. Положение этого раздела на странице заблокировано в зависимости от того, где он был добавлен в файл макета или шаблон.
Этот подход чаще всего используется для содержимого и компонентов, которые всегда должны быть видимыми, таких как заголовки, нижние колонтитулы и панели объявлений. Чтобы увидеть пример этого на Dawn, вы можете проверить файл theme.liquid, где статическая панель объявлений, разделы верхнего и нижнего колонтитула добавлены с помощью тега section .
Расширение возможностей для творчества
Теперь, когда вы узнали, как создавать и добавлять разделы в свои темы, вы можете создавать бесконечные варианты для магазинов ваших клиентов.
 И этот след — это сторона многоугольника, который образовывает сечение.
И этот след — это сторона многоугольника, который образовывает сечение.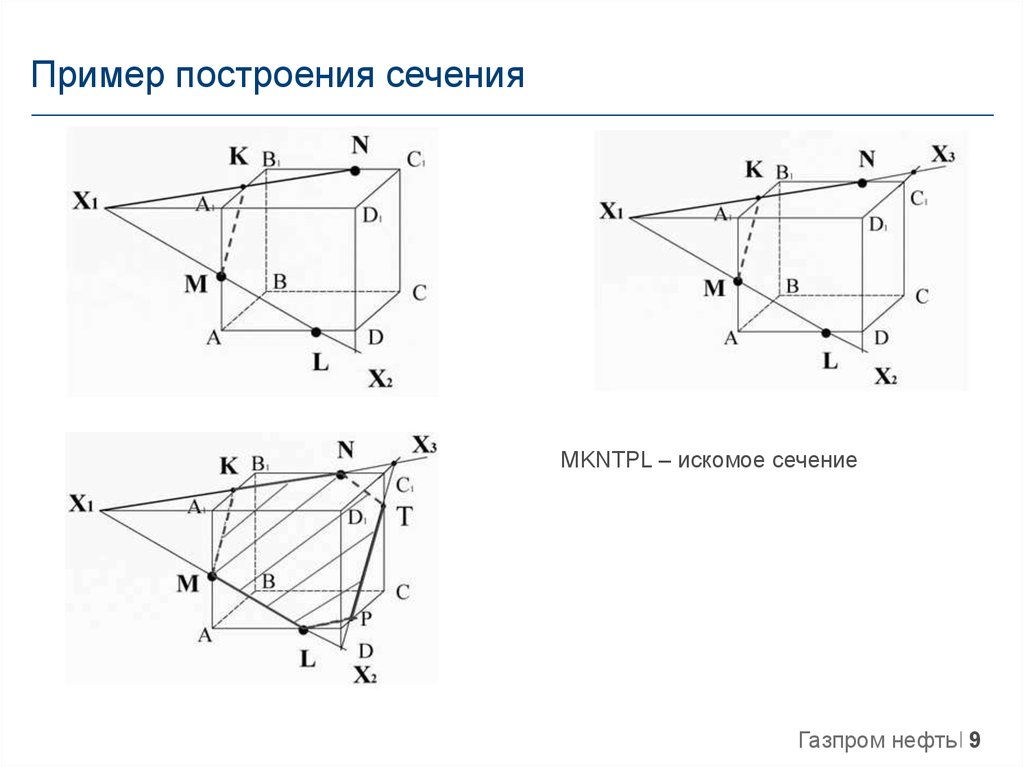 Это может быть удобно в случаях, когда метод следов невозможно или трудно применить.
Это может быть удобно в случаях, когда метод следов невозможно или трудно применить. 